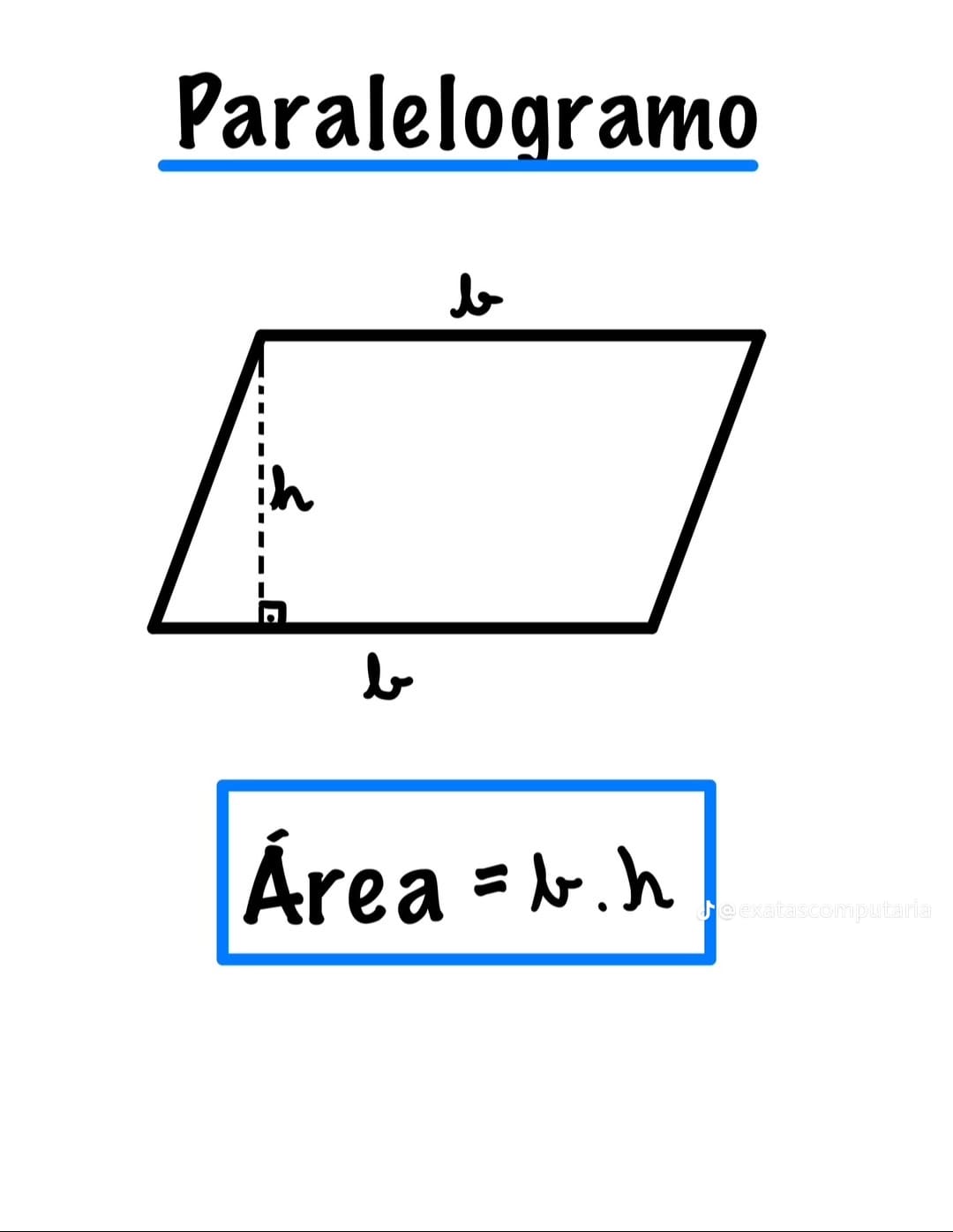
Área do Paralelogramo \(A=b\cdot h\)
Fórmula base × altura, versão trigonométrica com seno e forma com as diagonais. Exemplos resolvidos e exercícios com gabarito.
Fórmula principal
\[ A=b\cdot h \]
Escolha uma base \(b\) e use a altura \(h\) correspondente (perpendicular a essa base).
Como obter a altura \(h\)
- Interna em paralelogramos “mais retos”.
- Externa quando as laterais são muito inclinadas (prolongue a base e trace a perpendicular).
- Com seno: se dois lados \(a\) e \(b\) formam ângulo \(\theta\), então \(h=a\sin\theta\).
Outras expressões equivalentes
\[ A=a\,b\,\sin(\theta)\quad (\text{ângulo entre os lados } a \text{ e } b) \]
\[ A=\frac{d_1\,d_2\,\sin(\varphi)}{2}\quad (\text{ângulo } \varphi \text{ entre as diagonais}) \]
Casos particulares: se \(\varphi=90^\circ\), \(A=\frac{d_1d_2}{2}\) (retângulos, quadrados, losangos).
Veja também: ENEM Matemática • Mapas Mentais • Banco de Questões
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática e tenha um resumo enxuto de Geometria (áreas, perímetros, trigonometria e mais).
Exemplos resolvidos
Exemplo 1 Base × altura
Num paralelogramo, \(b=12\,\text{cm}\) e \(h=7\,\text{cm}\). Calcule a área.
Ver solução
\(=12\cdot 7\)
\(=84\,\text{cm}^2\).
Exemplo 2 Com seno do ângulo
Os lados medem \(a=10\) e \(b=14\) e o ângulo entre eles é \(\theta=30^\circ\). Encontre a área.
Ver solução
\(=10\cdot 14\cdot \sin30^\circ\)
\(=140\cdot 0{,}5\)
\(=70\).
Exemplo 3 Pelas diagonais
As diagonais medem \(d_1=20\) e \(d_2=16\) e o ângulo entre elas é \(\varphi=60^\circ\). Calcule a área (aprox.).
Ver solução
\(=\dfrac{20\cdot 16\cdot \sin60^\circ}{2}\)
\(=\dfrac{320\cdot \frac{\sqrt{3}}{2}}{2}\)
\(=160\cdot \dfrac{\sqrt{3}}{2}\)
\(\approx 160\cdot 0{,}8660\)
\(\approx 138{,}56\).
Exemplo 4 Encontrando a base
Sabendo que \(A=96\) e \(h=8\), determine \(b\).
Ver solução
\(=\dfrac{96}{8}\)
\(=12\).
Exercícios de múltipla escolha (com gabarito)
Enunciados claros e soluções com os passos um abaixo do outro após cada “=”.
1) Em um paralelogramo, \(b=18\,\text{cm}\) e \(h=5\,\text{cm}\). A área é:
Gabarito e solução
\(=18\cdot 5\)
\(=90\,\text{cm}^2\Rightarrow\) Letra C.
2) A área é \(132\,\text{m}^2\) e \(b=12\,\text{m}\). A altura \(h\) vale:
Gabarito e solução
\(=\dfrac{132}{12}\)
\(=11\,\text{m}\Rightarrow\) Letra C.
3) Lados \(a=9\) e \(b=12\) com \(\theta=30^\circ\). A área é:
Gabarito e solução
\(=9\cdot 12\cdot \sin30^\circ\)
\(=108\cdot 0{,}5\)
\(=54\Rightarrow\) Letra B.
4) Diagonais \(d_1=10\) e \(d_2=14\) com ângulo \(\varphi=45^\circ\). A área (aprox.) é:
Gabarito e solução
\(=\dfrac{10\cdot 14\cdot \sin45^\circ}{2}\)
\(=\dfrac{140\cdot \frac{\sqrt2}{2}}{2}\)
\(=70\cdot \dfrac{\sqrt2}{2}\)
\(\approx 70\cdot 0{,}7071\)
\(\approx 49{,}5\Rightarrow\) Letra B.
5) Para \(a=15\), \(b=10\) e \(\theta=\dfrac{\pi}{6}\) rad, a área é:
Gabarito e solução
\(A=a\,b\,\sin\theta\)
\(=15\cdot 10\cdot 0{,}5\)
\(=75\Rightarrow\) Letra C.
6) Um paralelogramo possui lados \(8\) e \(10\) e área \(64\). O ângulo \(\theta\) entre os lados vale (em graus, aprox.):
Gabarito e solução
\(=\dfrac{64}{8\cdot 10}\)
\(=\dfrac{64}{80}=0{,}8\)
\(\theta\approx \arcsin(0{,}8)\approx 53{,}1^\circ\Rightarrow\) Letra C.
7) Em um retângulo (caso particular de paralelogramo), \(a=13\) e \(b=9\). A área é:
Gabarito e solução
\(=13\cdot 9\)
\(=117\Rightarrow\) Letra C.
8) Um terreno em forma de paralelogramo tem \(b=24\,\text{m}\) e \(h=18\,\text{m}\). O custo do piso é R$ 45,00 por m². O valor total é:
Gabarito e solução
\(=432\,\text{m}^2\).
Custo \(=432\cdot 45\)
\(=432\cdot 40 + 432\cdot 5\)
\(=17.280 + 2.160\)
\(=19.440\Rightarrow\) Letra B.
Dicas finais
- Se não tiver a altura, use \(A=a\,b\,\sin\theta\) ou a forma com diagonais.
- A altura é sempre perpendicular à base (mesmo que fora da figura).
- Unidades importam: converta cm↔m antes de multiplicar.












