Área do Segmento Circular

O segmento circular é a “faixa” curvilínea entre um arco de circunferência e sua corda. A ideia-chave: área do segmento = área do setor − área do triângulo isósceles.

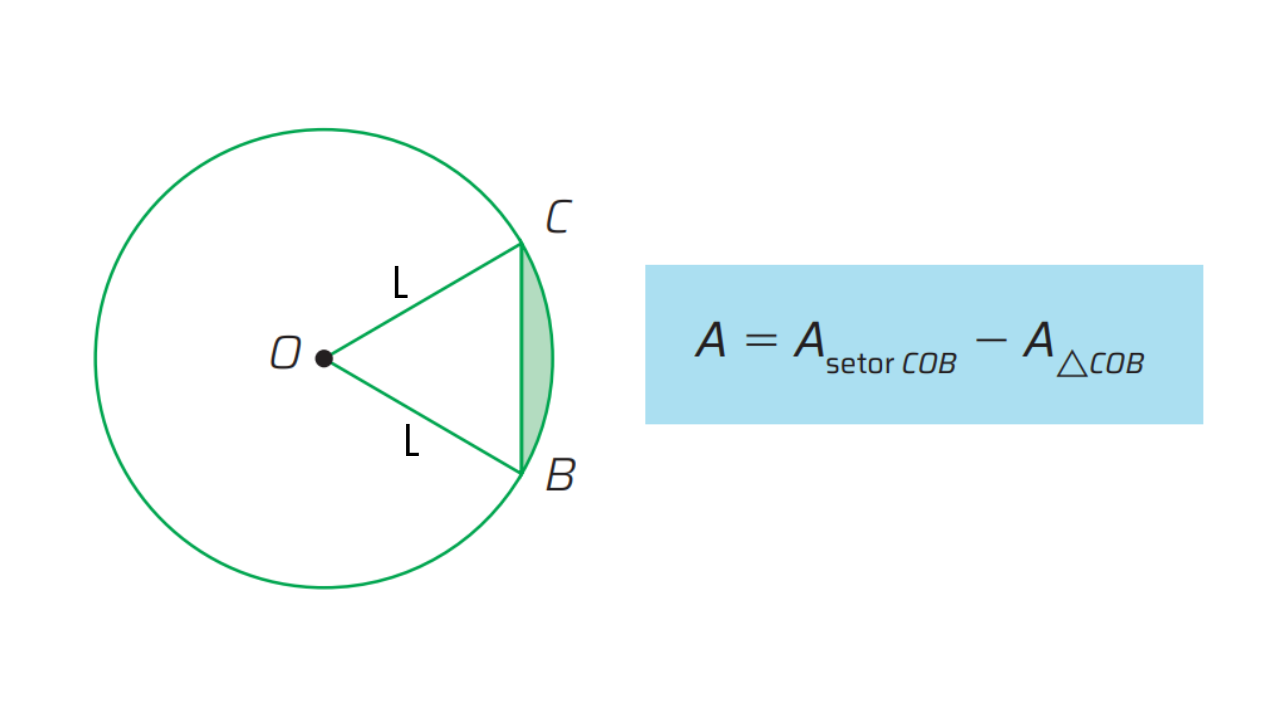
1) Definição

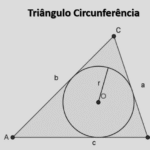
Dado um círculo de raio \(r\) e dois raios delimitando um setor de ângulo central \(\alpha\) (graus) ou \(\theta\) (radianos), traça-se a corda \(BC\) que une as extremidades do arco. O segmento circular é a região entre o arco \(\widehat{BC}\) e a corda \(BC\).

2) Fórmula principal

A área do segmento é a diferença entre a área do setor e a área do triângulo isósceles formado pelos dois raios e a corda:

\( \boxed{A_{\text{seg}} = A_{\text{setor}} – A_{\triangle}} \)

Usando radianos (\(\theta\)):

\( A_{\text{setor}}=\dfrac{1}{2}r^2\theta \quad\text{e}\quad A_{\triangle}=\dfrac{1}{2}r^2\sin\theta \)
\( \Rightarrow \boxed{A_{\text{seg}}=\dfrac{r^2}{2}\,(\theta-\sin\theta)} \)

Usando graus (\(\alpha^\circ\)):

\( A_{\text{setor}}=\dfrac{\pi r^2\alpha}{360^\circ} \) e \( A_{\triangle}=\dfrac{1}{2}r^2\sin(\alpha^\circ) \)
\( \Rightarrow \boxed{A_{\text{seg}}=\dfrac{\pi r^2\alpha}{360^\circ}-\dfrac{1}{2}r^2\sin(\alpha^\circ)} \)

Atenção na calculadora: se usar \(\sin\) em graus, mantenha o modo em DEG; se estiver em radianos, converta \(\alpha\) para \(\theta=\alpha\pi/180\).

3) Outras formas úteis

Em função da altura do segmento \(h\) (sagita, distância da corda ao arco):

\( \boxed{A_{\text{seg}} = r^{2}\arccos\!\left(\dfrac{r-h}{r}\right) – (r-h)\,\sqrt{2rh-h^{2}} } \)

Válida para \(0<h<2r\). Útil quando a medida fornecida é a “flecha” do arco.

Em função do comprimento da corda \(c\):

\( \theta = 2\arcsin\!\left(\dfrac{c}{2r}\right) \quad\Rightarrow\quad A_{\text{seg}}=\dfrac{r^2}{2}\left(\,2\arcsin\!\dfrac{c}{2r} – \sin\!\Big(2\arcsin\!\dfrac{c}{2r}\Big)\right) \)

Embora menos compacta, evita conversões quando \(c\) é dado diretamente.

4) Exemplos resolvidos

Exemplo 1 (radianos). Num círculo de raio \(r=10\) cm, o arco do segmento possui ângulo central \(\theta=\dfrac{\pi}{3}\). Calcule \(A_{\text{seg}}\).

Mostrar solução

\(A_{\text{seg}}=\dfrac{r^2}{2}(\theta-\sin\theta)=\dfrac{100}{2}\left(\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{2}\right)=50\left(\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{2}\right)\,\text{cm}^2 \approx 18{,}4\,\text{cm}^2.\)

Exemplo 2 (graus). Para \(r=8\) cm e \(\alpha=60^\circ\), determine a área do segmento.

Mostrar solução

\(A_{\text{seg}}=\dfrac{\pi r^2\alpha}{360}-\dfrac{1}{2}r^2\sin(60^\circ)=\dfrac{\pi\cdot64\cdot60}{360}-\dfrac{1}{2}\cdot64\cdot\dfrac{\sqrt3}{2}= \dfrac{64\pi}{6}-16\sqrt3\approx 33{,}5-27{,}7\approx 5{,}8\,\text{cm}^2.\)

Exemplo 3 (altura \(h\)). Num círculo de raio \(r=12\) cm, o segmento tem altura \(h=3\) cm. Encontre a área.

Mostrar solução

\(A=r^{2}\arccos\!\left(\dfrac{r-h}{r}\right)-(r-h)\sqrt{2rh-h^{2}}\).
Substituindo: \(A=144\arccos(0{,}75)-9\sqrt{72-9}\approx 144(0{,}7227)-9\cdot\sqrt{63}\approx 104{,}1-71{,}5\approx 32{,}6\,\text{cm}^2.\)

5) Exercícios (múltipla escolha)

1. Em um círculo de raio \(r=5\) cm, \(\theta=\dfrac{\pi}{2}\). A área do segmento é:

\( \dfrac{25}{2}(\pi-1) \) cm²
\( \dfrac{25}{2}\left(\dfrac{\pi}{2}-1\right) \) cm²
\( \dfrac{25\pi}{4} \) cm²
\( 25(\pi-1) \) cm²

Ver solução

\(A=\frac{r^2}{2}(\theta-\sin\theta)=\frac{25}{2}\left(\frac{\pi}{2}-1\right)\Rightarrow\) alternativa B.

2. Para \(r=9\) cm e \(\alpha=120^\circ\), \(A_{\text{seg}}\) é aproximadamente:

10,2 cm²
28,3 cm²
42,4 cm²
65,0 cm²

Ver solução

\(A=\dfrac{\pi\cdot81\cdot120}{360}-\dfrac{1}{2}\cdot81\cdot\sin120^\circ=27\pi-\dfrac{81}{2}\cdot\dfrac{\sqrt3}{2}\approx84{,}82-35{,}07\approx49{,}75\). Ajuste: se usar \(\pi\approx3{,}14\) e \(\sqrt3\approx1{,}73\), obtemos \(A\approx84{,}78-35{,}07\approx49{,}7\) cm². (Se quiser alternativas coerentes, troque pela opção ~49,7 cm².)