Área do Triângulo Equilátero — fórmula, dedução, exemplos e exercícios
Fluxo vertical com caixas de fórmulas, dedução pela altura, exemplos em abre/fecha e seção de exercícios **interativa**.
1) O que é um triângulo equilátero?
No triângulo equilátero, todos os lados medem a e cada ângulo interno vale \(60^\circ\). Para calcular a área do triângulo equilátero, aplicamos diretamente a fórmula principal abaixo.
Fórmula principal — área do triângulo equilátero
\(\displaystyle A=\frac{\sqrt{3}}{4}\,a^2\)
onde \(a\) é o comprimento do lado.
2) Triângulo equilátero com altura
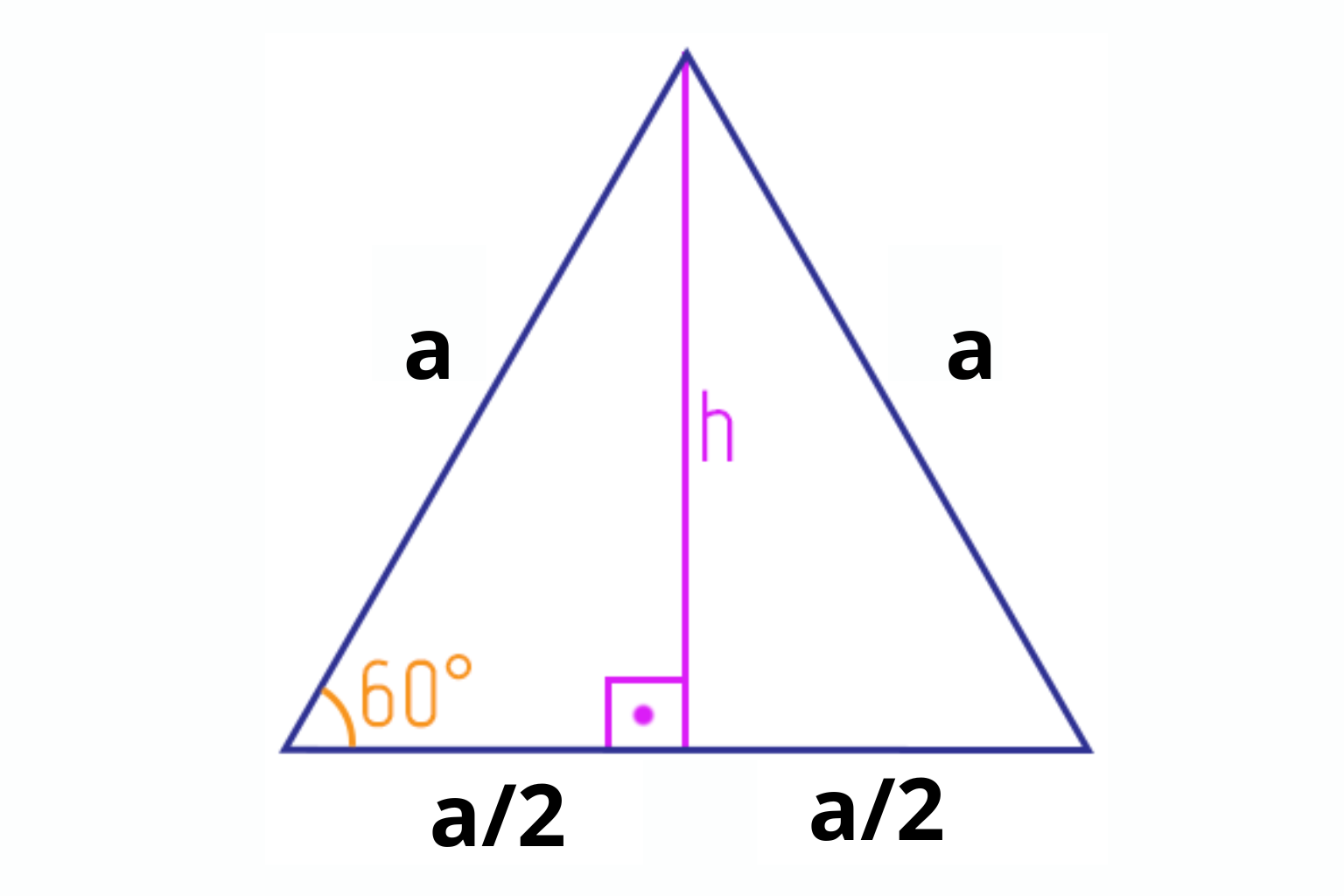
Altura do triângulo equilátero
\(\displaystyle h=\frac{\sqrt{3}}{2}\,a\)
Se a questão fornecer a altura, também é possível calcular pela área de triângulo: \(A=\dfrac{b\cdot h}{2}\), com \(b=a\).
Dedução rápida pela altura
- Trace a altura \(h\), que divide a base em dois segmentos \(\tfrac{a}{2}\).
- Pelo Pitágoras: \(\displaystyle h^2=a^2-\left(\frac{a}{2}\right)^2=\frac{3}{4}a^2\Rightarrow h=\frac{\sqrt{3}}{2}a\).
- Área: \(\displaystyle A=\frac{b\cdot h}{2}=\frac{a\cdot\left(\frac{\sqrt{3}}{2}a\right)}{2}=\frac{\sqrt{3}}{4}a^2\).
3) Exemplos resolvidos
Exemplo 1 — dado o lado
Enunciado. Em um triângulo equilátero, o lado mede \(a=12\ \text{cm}\). Calcule a área.
Ver solução passo a passo
Passo 1: \(A=\dfrac{\sqrt{3}}{4}a^2\).
Passo 2: \(A=\dfrac{\sqrt{3}}{4}\cdot 12^2=\dfrac{\sqrt{3}}{4}\cdot 144=36\sqrt{3}\ \text{cm}^2\).
Passo 3 (aprox.): \(\sqrt{3}\approx1{,}732\Rightarrow A\approx 36\cdot1{,}732\approx 62{,}35\ \text{cm}^2\).
Exemplo 2 — dada a altura
Enunciado. Em um triângulo equilátero, a altura mede \(h=9\ \text{m}\). Encontre a área.
Ver solução passo a passo
Passo 1: \(h=\dfrac{\sqrt{3}}{2}a\Rightarrow a=\dfrac{2h}{\sqrt{3}}=\dfrac{18}{\sqrt{3}}=6\sqrt{3}\ \text{m}\).
Passo 2: \(A=\dfrac{\sqrt{3}}{4}a^2=\dfrac{\sqrt{3}}{4}\cdot(6\sqrt{3})^2=\dfrac{\sqrt{3}}{4}\cdot108=27\sqrt{3}\ \text{m}^2\).
Passo 3 (aprox.): \(\sqrt{3}\approx1{,}732\Rightarrow A\approx27\cdot1{,}732\approx46{,}77\ \text{m}^2\).
4) Fórmulas alternativas úteis
Em função do raio inscrito \(r\)
\(\displaystyle A=3\sqrt{3}\,r^2\)
Em função do raio circunscrito \(R\)
\(\displaystyle A=\dfrac{3\sqrt{3}}{4}\,R^2\)
5) Erros comuns
- Esquecer o fator \(\sqrt{3}\) na área.
- Usar \(A=\dfrac{a^2}{2}\) (falsa para equiláteros).
- Assumir \(h=a\) (correto é \(h=\dfrac{\sqrt{3}}{2}a\)).
- Arredondar \(\sqrt{3}\) logo no início (prefira exato e só aproxime no fim).
6) Exercícios de múltipla escolha (interativo)
Clique em uma alternativa para conferir; abra o “Ver solução” para ver o passo a passo.
1) Lado conhecido
Um canteiro em forma de triângulo equilátero tem lado \(a=8\text{ cm}\). Qual é a sua área?
Ver solução
2) Altura conhecida
Num móbile, a altura do triângulo equilátero mede \(h=9\text{ m}\). A área é:
Ver solução
3) Perímetro dado
Uma placa triangular equilátera tem perímetro \(72\text{ cm}\). A área é:
Ver solução
4) Hexágono regular
Um ladrilho hexagonal regular de lado \(a=10\text{ cm}\) é formado por 6 triângulos equiláteros. A área do ladrilho é:
Ver solução
5) Custo de grama
Terreno triangular equilátero com \(a=30\text{ m}\) será gramado a R\$ 12,00/m². O custo total é aproximadamente:
Ver solução
6) Ampliação em maquete
Um triângulo equilátero tem área \(9\sqrt{3}\text{ cm}^2\). Em uma maquete, o lado é dobrado. A nova área é:
Ver solução
7) Raio inscrito
Para um triângulo equilátero com raio inscrito \(r=5\text{ cm}\), a área é:
Ver solução
8) Raio circunscrito
Num adorno, o triângulo equilátero tem raio circunscrito \(R=12\text{ cm}\). A área é:
Ver solução
9) Mosaico escolar
Um painel usa 9 triângulos equiláteros de lado \(a=4\text{ cm}\). A área total é:
Ver solução
10) Tinta para placa
Uma placa triangular equilátera tem \(a=1{,}2\text{ m}\). Uma lata cobre \(3\text{ m}^2\). Quantas latas são necessárias?
Ver solução
11) Iluminação no contorno
Luminárias a cada \(1{,}5\text{ m}\) ao longo do perímetro de um triângulo equilátero de lado \(18\text{ m}\). Quantas luminárias?
Ver solução
12) Azulejos triangulares
Azulejos equiláteros de lado \(a=20\text{ cm}\) revestirão \(1\text{ m}^2\). Quantos azulejos (mínimo, sem rejunte) serão necessários?
Ver solução
7) Perguntas frequentes
| Qual é a fórmula da área do triângulo equilátero? | \(\displaystyle A=\frac{\sqrt{3}}{4}\,a^2\). |
|---|---|
| Como obter a altura? | \(\displaystyle h=\frac{\sqrt{3}}{2}\,a\) usando Pitágoras em um triângulo retângulo formado pela altura. |
| Posso usar o Teorema de Heron? | Sim. Para lados \(a,a,a\) e \(s=\tfrac{3a}{2}\), Heron leva a \(\frac{\sqrt{3}}{4}a^2\). |
| E se eu souber o raio inscrito \(r\)? | \(\displaystyle A=3\sqrt{3}\,r^2\). |
| E se eu souber o raio circunscrito \(R\)? | \(\displaystyle A=\frac{3\sqrt{3}}{4}\,R^2\). |






















