Área do Triângulo Retângulo — fórmulas, deduções, exemplos e exercícios
Guia vertical para quem busca area do triangulo retangulo, área do triângulo retângulo, area de um triangulo retângulo, area triangulo retângulo, calcular triângulo retângulo e fórmula do triângulo retângulo.
1) O que é um triângulo retângulo?
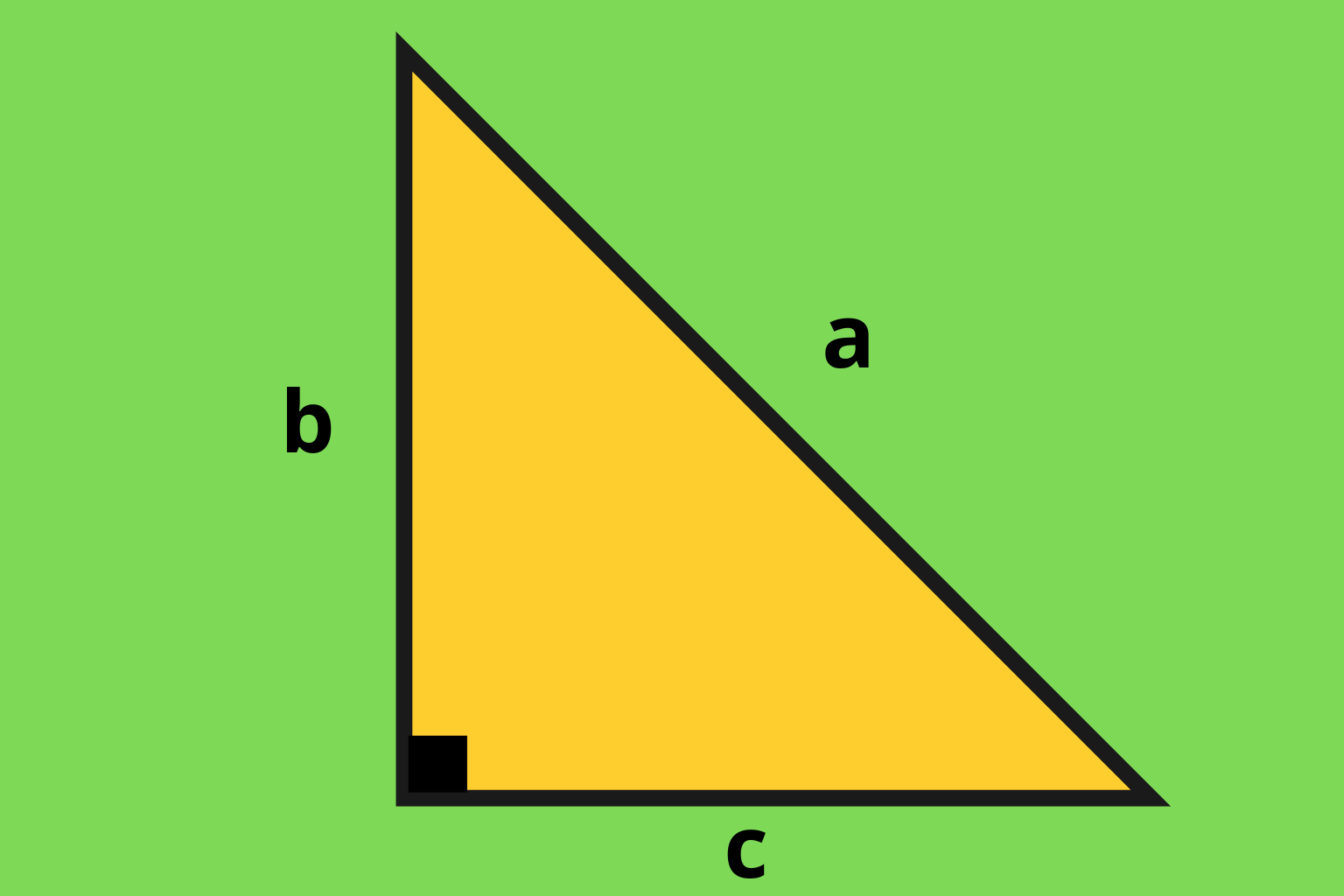
Para calcular área do triângulo retângulo com rapidez, lembre-se: os catetos já são base e altura (são perpendiculares).
Fórmula principal — área do triângulo retângulo
\(\displaystyle A=\frac{a\cdot b}{2}\)
com \(a\) e \(b\) os comprimentos dos catetos.
Variações úteis (quando a questão não dá os dois catetos)
- Hipotenusa e altura à hipotenusa \(h_c\): \(\displaystyle A=\frac{c\cdot h_c}{2}\).
- Hipotenusa e ângulo agudo \(\alpha\): \(\displaystyle A=\frac{1}{2}\,c^2\sin\alpha\cos\alpha=\frac{1}{4}\,c^2\sin(2\alpha)\).
- Um cateto \(a\) e ângulo \(\alpha\):
- \(\alpha\) adjacente a \(a\): cateto oposto \(=a\tan\alpha\Rightarrow \displaystyle A=\frac{1}{2}a^2\tan\alpha\).
- \(\alpha\) oposto a \(a\): cateto adjacente \(=\dfrac{a}{\tan\alpha}\Rightarrow \displaystyle A=\frac{1}{2}\,\frac{a^2}{\tan\alpha}\).
- Semiperímetro \(s\) e raio da circunferência inscrita \(r\): todo triângulo satisfaz \(\displaystyle A=r\,s\). No retângulo, \(\displaystyle r=\frac{a+b-c}{2}\).
Por que \(A=\dfrac{a\cdot b}{2}\)? (dedução rápida)
- Os catetos são perpendiculares \(\Rightarrow\) funcionam como base e altura.
- Em qualquer triângulo, \(\displaystyle A=\dfrac{\text{base}\times\text{altura}}{2}\).
- Tomando base \(=a\) e altura \(=b\), obtemos \(\displaystyle A=\dfrac{a\,b}{2}\).
2) Exemplos resolvidos (passo a passo)
Exemplo 1 — catetos dados
Enunciado. Num triângulo retângulo, \(a=6\ \text{cm}\) e \(b=8\ \text{cm}\). Calcule a área.
Ver solução
Exemplo 2 — hipotenusa e altura à hipotenusa
Enunciado. A hipotenusa mede \(c=13\ \text{cm}\) e a altura à hipotenusa \(h_c=4{,}8\ \text{cm}\). Calcule a área.
Ver solução
Exemplo 3 — cateto e ângulo
Enunciado. O cateto adjacente ao ângulo \(\alpha=30^\circ\) mede \(a=10\ \text{m}\). Encontre a área.
Ver solução
\(A=\dfrac{a\cdot b}{2}=\dfrac{10\cdot\frac{10}{\sqrt{3}}}{2}=\dfrac{50}{\sqrt{3}}\ \text{m}^2\approx 28{,}87\ \text{m}^2.\)
Exemplo 4 — perímetro e um cateto
Enunciado. Em um triângulo retângulo com perímetro \(P=48\ \text{cm}\), um cateto mede \(a=14\ \text{cm}\). Calcule a área.
Ver solução (equações e numérico)
Do perímetro: \(a+b+c=48\Rightarrow b+\sqrt{196+b^2}=34\).
Isolando: \(\sqrt{196+b^2}=34-b\Rightarrow 196+b^2=1156-68b+b^2\Rightarrow b=\dfrac{960}{68}\approx 14{,}1176\ \text{cm}.\)
Área: \(A=\dfrac{a\,b}{2}\approx\dfrac{14\cdot14{,}1176}{2}\approx 98{,}82\ \text{cm}^2.\)
3) Erros comuns ao calcular triângulo retângulo
- Usar a hipotenusa como “base” na fórmula \(A=\dfrac{\text{base}\cdot\text{altura}}{2}\). Nos retângulos, a base/altura são os catetos.
- Trocar oposto/adjacente nos usos de \(\sin\) e \(\cos\), gerando áreas incoerentes.
- Arredondar \(\sqrt{3}\), \(\tan\theta\) etc. logo no início. Prefira o valor exato e só aproxime no fim.
- Usar \(A=\dfrac{c^2}{2}\) (falso). Só vale \(A=\dfrac{c\,h_c}{2}\) se \(h_c\) for a altura à hipotenusa.
4) Exercícios de múltipla escolha (interativo)
Clique em uma alternativa para conferir; abra “Ver solução” para ver o passo a passo.
1) Catetos dados
Num triângulo retângulo, \(a=9\ \text{cm}\) e \(b=12\ \text{cm}\). Qual é a área?
Ver solução
2) Hipotenusa e ângulo
Em um triângulo retângulo, \(c=10\ \text{m}\) e \(\alpha=45^\circ\). A área é:
Ver solução
3) Altura à hipotenusa
Para \(c=20\ \text{cm}\) e altura à hipotenusa \(h_c=7\ \text{cm}\), a área vale:
Ver solução
4) Hipotenusa conhecida e um cateto
Num triângulo retângulo, \(c=13\ \text{m}\) e \(a=5\ \text{m}\). A área é:
Ver solução
5) Isósceles retângulo com perímetro fixo
Se \(a=b\) e o perímetro é \(P=60\ \text{cm}\), a área é aproximadamente:
Ver solução
6) Cateto e ângulo adjacente
O cateto adjacente ao ângulo \(\alpha=30^\circ\) mede \(a=10\ \text{m}\). A área é aproximadamente:
Ver solução
\(A=\dfrac{a\,b}{2}=\dfrac{10\cdot(10/\sqrt{3})}{2}=\dfrac{50}{\sqrt{3}}\approx \mathbf{28{,}87}\ \text{m}^2.\)
7) Rampa (aplicação prática)
Uma rampa triangular tem base \(2{,}4\ \text{m}\) e altura \(0{,}9\ \text{m}\). A área é:
Ver solução
8) Azulejos (planejamento)
Azulejos em forma de triângulo retângulo com \(a=30\ \text{cm}\) e \(b=40\ \text{cm}\) revestirão \(3\ \text{m}^2\). Quantas peças (mínimo, sem rejunte) são necessárias?
Ver solução
\(3/0{,}06=\mathbf{50}\) peças.
9) Hipotenusa e ângulo 60°
Para \(c=14\ \text{cm}\) e \(\alpha=60^\circ\), a área vale (exata):
Ver solução
10) Perímetro 36 (tripla pitagórica)
Um triângulo retângulo tem perímetro \(P=36\ \text{cm}\) e é semelhante à tripla \((3,4,5)\). A área é:
Ver solução
\(A=\dfrac{9\cdot12}{2}=\mathbf{54}\ \text{cm}^2.\)
11) Um cateto e ângulo adjacente (60°)
O cateto adjacente vale \(a=7\ \text{m}\) e \(\alpha=60^\circ\). A área aproximada é:
Ver solução
\(A=\dfrac{a\,b}{2}=\dfrac{7\cdot7\sqrt{3}}{2}=\dfrac{49\sqrt{3}}{2}\approx \mathbf{42{,}43}\ \text{m}^2.\)
12) Hipotenusa 26 e cateto 10
Num triângulo retângulo com \(c=26\ \text{cm}\) e \(a=10\ \text{cm}\), a área é:
Ver solução
5) Perguntas frequentes
| Qual é a fórmula da área do triângulo retângulo? | \(\displaystyle A=\frac{a\cdot b}{2}\), com \(a\) e \(b\) os catetos. |
|---|---|
| Como calcular área do triângulo retângulo usando a hipotenusa? | Use a altura à hipotenusa \(h_c\): \(\displaystyle A=\frac{c\cdot h_c}{2}\). Com ângulo \(\alpha\): \(\displaystyle A=\frac{1}{4}c^2\sin(2\alpha)\). |
| Existe relação com o raio da circunferência inscrita \(r\)? | Sim. Para qualquer triângulo, \(\displaystyle A=r\,s\) (semiperímetro \(s\)). Em triângulo retângulo, \(\displaystyle r=\frac{a+b-c}{2}\). |
| Qual “fórmula do triângulo retângulo” mais aparece no ENEM? | \(\displaystyle A=\dfrac{a\cdot b}{2}\) — muito usada em problemas práticos (piso, telhado, jardinagem, maquetes). |