Áreas de Regiões Triangulares — Fórmulas, Exemplos e Exercícios

O cálculo da área do triângulo é um dos temas mais pesquisados em Matemática. Há diversas formas de encontrá-la — desde a fórmula clássica da base e altura até métodos mais avançados como a Fórmula de Heron e as expressões envolvendo o raio da circunferência inscrita e a circunferência circunscrita.

Neste artigo completo do Matemática Hoje, você vai descobrir todas as fórmulas usadas para calcular a área de triângulos, aprender como aplicá-las passo a passo e resolver exercícios práticos que aparecem em provas de Matemática no ENEM e em concursos públicos.

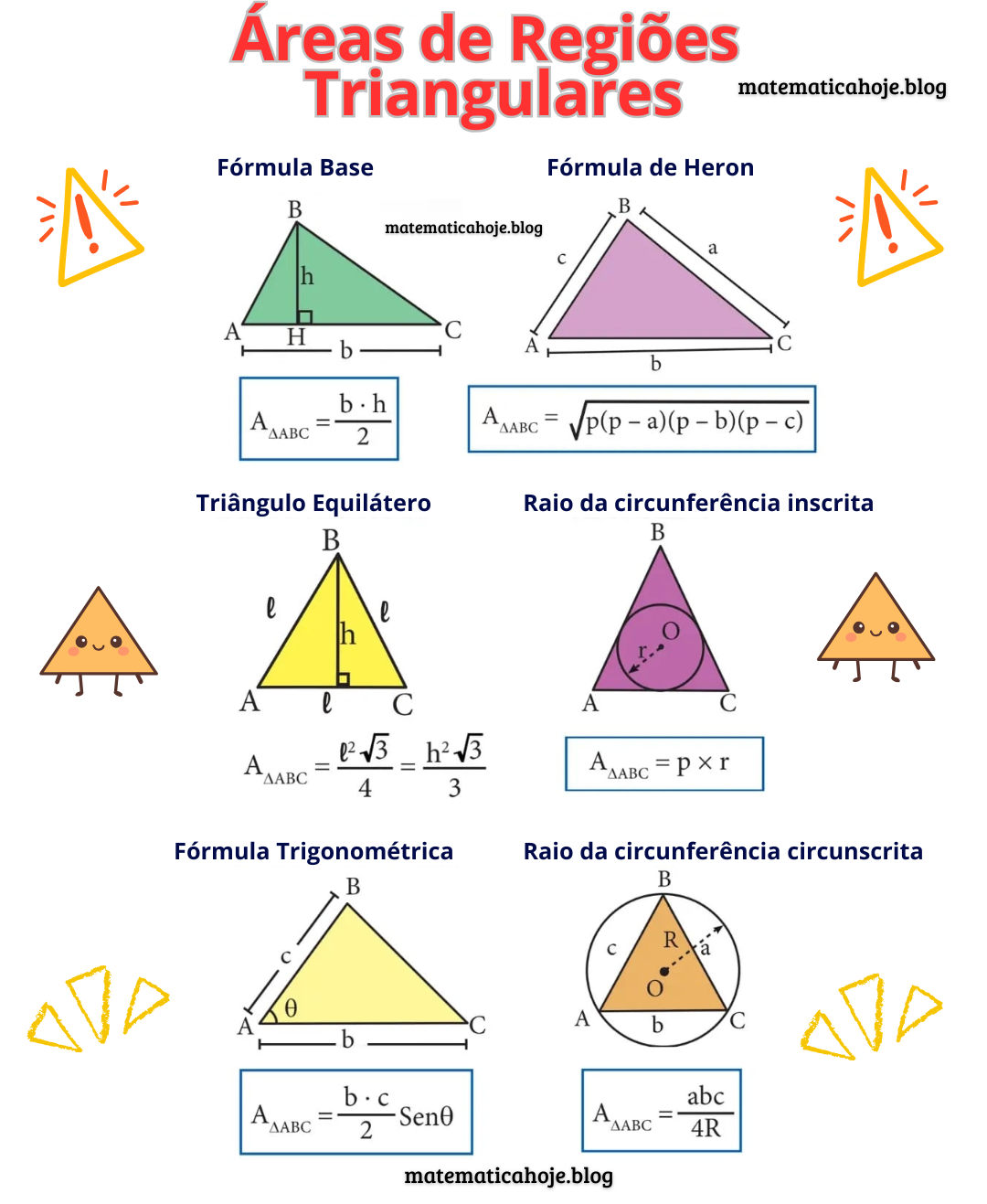
Fórmulas da Área do Triângulo - Matemática Hoje

📘 Baixe gratuitamente nosso eBook de Fórmulas Matemáticas — um guia completo para revisar todos os conteúdos de geometria!

1. Fórmula Base — Base e Altura

Essa é a fórmula mais conhecida e prática para calcular a área de qualquer triângulo, desde que se conheça a medida da base e da altura correspondente.

\( A_{\triangle} = \frac{b \cdot h}{2} \)

Exemplo: Um triângulo tem base \( b = 12 \,cm \) e altura \( h = 8 \,cm \).
Calcule a área.

\( A = \frac{12 \cdot 8}{2} \)
= \( \frac{96}{2} \)
= 48 cm²

2. Fórmula de Heron — Usando os Três Lados

Quando as medidas da base e da altura não são conhecidas, é possível calcular a área usando apenas os três lados \( a \), \( b \) e \( c \). Para isso, utiliza-se o semiperímetro \( p = \frac{a+b+c}{2} \).

\( A_{\triangle} = \sqrt{p(p – a)(p – b)(p – c)} \)

Exemplo: Para um triângulo com lados \( a = 5 \), \( b = 6 \) e \( c = 7 \):
\( p = \frac{5 + 6 + 7}{2} = 9 \)
\( A = \sqrt{9(9-5)(9-6)(9-7)} \)
= \( \sqrt{9 \cdot 4 \cdot 3 \cdot 2} \)
= \( \sqrt{216} \)
= 14,7 cm² (aproximadamente)

3. Triângulo Equilátero

Quando os três lados do triângulo são iguais, a área pode ser calculada com uma fórmula simplificada.

\( A_{\triangle} = \frac{l^2 \sqrt{3}}{4} \)

Exemplo: Um triângulo equilátero tem lado \( l = 10 \,cm \).
\( A = \frac{10^2 \sqrt{3}}{4} \)
= \( \frac{100 \sqrt{3}}{4} \)
= 25√3 cm²
(aproximadamente 43,3 cm²)

4. Raio da Circunferência Inscrita (Inrário)

Em alguns problemas geométricos, a área também pode ser calculada conhecendo o raio da circunferência inscrita \( r \) e o semiperímetro \( p \).

\( A_{\triangle} = p \cdot r \)

Exemplo: Dado um triângulo com semiperímetro \( p = 12 \) e raio da circunferência inscrita \( r = 3 \), temos:
\( A = 12 \cdot 3 \)
= 36 cm²

🎯 Estude com nossos Mapas Mentais de Matemática — visualize todas as fórmulas de Geometria em um só lugar!

5. Fórmula Trigonométrica

Quando se conhece dois lados e o ângulo entre eles, a fórmula trigonométrica é ideal para encontrar a área.

\( A_{\triangle} = \frac{b \cdot c \cdot \sin(\theta)}{2} \)

Exemplo: Para um triângulo com lados \( b = 10 \), \( c = 8 \) e ângulo \( \theta = 60° \):
\( A = \frac{10 \cdot 8 \cdot \sin(60°)}{2} \)
= \( 40 \cdot \frac{\sqrt{3}}{2} \)
= 20√3 cm²
(aproximadamente 34,6 cm²)

6. Raio da Circunferência Circunscrita

Quando o triângulo está inscrito em uma circunferência de raio \( R \), a área é calculada pela fórmula:

\( A_{\triangle} = \frac{a \cdot b \cdot c}{4R} \)

Exemplo: Um triângulo tem lados \( a = 7 \), \( b = 8 \), \( c = 9 \) e raio da circunferência circunscrita \( R = 5 \):
\( A = \frac{7 \cdot 8 \cdot 9}{4 \cdot 5} \)
= \( \frac{504}{20} \)
= 25,2 cm²

7. Exercícios para Praticar

Experimente resolver os desafios abaixo:

Calcule a área de um triângulo com base 15 cm e altura 10 cm.
Encontre a área de um triângulo equilátero de lado 12 cm.
Determine a área de um triângulo com lados 5 cm, 6 cm e 8 cm (use a Fórmula de Heron).

Depois, confira as respostas no Banco de Questões de Matemática — centenas de exercícios resolvidos por tema.

📘 Veja também: Coleção 10 eBooks de Matemática — teoria, exemplos e questões de concursos.

Conclusão

Com essas seis fórmulas, é possível resolver qualquer problema que envolva área de triângulos — sejam equiláteros, isósceles ou escalenos. Dominar esses métodos é essencial para ir bem em provas de Matemática do ENEM e em exames de vestibulares e concursos.

Continue seus estudos com nossos materiais exclusivos: