Áreas do Retângulo

Área do Retângulo — fórmulas, exemplos e exercícios

Área do Retângulo

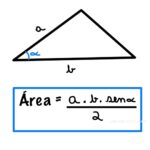
O retângulo é um paralelogramo com os quatro ângulos retos (90°). Seus lados adjacentes são as medidas a (comprimento) e b (largura). A área mede a “região pintada” do retângulo.

Retângulo com lados a e b
Retângulo: área \(A=a\cdot b\), perímetro \(P=2(a+b)\) e diagonal \(d=\sqrt{a^2+b^2}\).
Veja também: Área do Paralelogramo, Área do Quadrado (caso particular \(a=b\)), Área do Triângulo e Área do Trapézio.

Fórmulas essenciais (empilhadas)

\[ \textbf{1) Área:}\quad \boxed{A=a\cdot b} \]
\[ \textbf{2) Perímetro:}\quad \boxed{P=2(a+b)} \]
\[ \textbf{3) Diagonal (Pitágoras):}\quad \boxed{d=\sqrt{a^2+b^2}} \]
\[ \textbf{4) Área via diagonal e ângulo }\theta\text{ com }a:\quad \boxed{A=\tfrac{d^2}{2}\,\sin(2\theta)}\quad (\text{pois } a=d\cos\theta,\ b=d\sin\theta) \]

Exemplos resolvidos (situação-problema)

1

Piso de sala — medidas diretas

Uma sala retangular tem comprimento \(a=8\,\text{m}\) e largura \(b=5\,\text{m}\).

Dados
\(a=8\,\text{m}\), \(b=5\,\text{m}\).

Qual é a área do piso?

Ver solução
\[ \begin{aligned} A&=a\cdot b\\ &=8\cdot 5\\ &=\boxed{40\ \text{m}^2} \end{aligned} \]
2

Poster — diagonal conhecida

Um cartaz é retangular e tem diagonal \(d=13\,\text{m}\) (modelo ampliado) e largura \(b=5\,\text{m}\).

Dados
\(d=13\,\text{m}\), \(b=5\,\text{m}\).

Qual é a área do cartaz?

Ver solução
\[ \begin{aligned} a&=\sqrt{d^2-b^2}\\ &=\sqrt{13^2-5^2}\\ &=\sqrt{169-25}\\ &=\sqrt{144}\\ &=12\\[4pt] A&=a\cdot b=12\cdot 5=\boxed{60\ \text{m}^2} \end{aligned} \]
3

Jardim — a partir do perímetro

O contorno de um jardim retangular tem perímetro \(P=30\,\text{m}\) e o comprimento é \(a=8\,\text{m}\).

Dados
\(P=30\,\text{m}\), \(a=8\,\text{m}\).

Qual é a área do jardim?

Ver solução
\[ \begin{aligned} P&=2(a+b) \Rightarrow a+b=\tfrac{P}{2}=15\\ b&=15-8=7\\[4pt] A&=a\cdot b=8\cdot 7=\boxed{56\ \text{m}^2} \end{aligned} \]
4

Piso com lajotas — contagem de peças

Um piso mede \(6\,\text{m}\times 4\,\text{m}\). As lajotas são quadradas de \(30\,\text{cm}\times 30\,\text{cm}\).

Dados
Área do piso \(A=6\cdot 4=24\,\text{m}^2\); área da lajota \(0{,}30\cdot 0{,}30=0{,}09\,\text{m}^2\).

Quantas lajotas são necessárias (sem considerar perdas)?

Ver solução
\[ \begin{aligned} N&=\frac{A_{\text{piso}}}{A_{\text{lajota}}}\\ &=\frac{24}{0{,}09}\\ &=266{,}6\ldots\\ &\Rightarrow \boxed{267\ \text{lajotas}} \end{aligned} \]

Para perdas de corte, some 5–10%. Revise unidades em área do triângulo e paralelogramo.

Erros comuns (e como evitar)

  • Trocar unidade. Converta cm² ↔ m² corretamente (\(1\,\text{m}^2=10\,000\,\text{cm}^2\)).
  • Confundir perímetro com área. Perímetro soma bordas; área multiplica lados.
  • Diagonal. Use Pitágoras \(d=\sqrt{a^2+b^2}\). Se der \(d\) e um lado, ache o outro.

Exercícios (múltipla escolha)

1

Medidas diretas

Um quadro mede \(12\,\text{cm}\times 7\,\text{cm}\).

A área é:

  • A) \(72\ \text{cm}^2\)
  • B) \(80\ \text{cm}^2\)
  • C) 84 \(\text{cm}^2\)
  • D) \(90\ \text{cm}^2\)
Gabarito
\[ A=a b=12\cdot 7=\boxed{84\ \text{cm}^2}\ (\text{C}) \]
2

Com a diagonal

Num retângulo, \(d=25\,\text{cm}\) e um lado é \(7\,\text{cm}\).

A área do retângulo é:

  • A) \(150\ \text{cm}^2\)
  • B) 168 \(\text{cm}^2\)
  • C) \(175\ \text{cm}^2\)
  • D) \(196\ \text{cm}^2\)
Gabarito
\[ \begin{aligned} b&=\sqrt{25^2-7^2}=\sqrt{625-49}=\sqrt{576}=24\\ A&=7\cdot 24=\boxed{168\ \text{cm}^2}\ (\text{B}) \end{aligned} \]
3

A partir do perímetro

Um terreno retangular tem perímetro \(50\,\text{m}\) e comprimento \(18\,\text{m}\).

A área do terreno é:

  • A) \(108\ \text{m}^2\)
  • B) 126 \(\text{m}^2\)
  • C) \(144\ \text{m}^2\)
  • D) \(150\ \text{m}^2\)
Gabarito
\[ \begin{aligned} a+b&=\tfrac{P}{2}=25 \Rightarrow b=25-18=7\\ A&=18\cdot 7=\boxed{126\ \text{m}^2}\ (\text{B}) \end{aligned} \]
4

Descobrindo o perímetro

A fachada de um galpão retangular tem área \(96\,\text{m}^2\) e comprimento \(12\,\text{m}\).

O perímetro dessa fachada é:

  • A) \(36\ \text{m}\)
  • B) \( \mathbf{40\ \text{m}} \)
  • C) \(44\ \text{m}\)
  • D) \(48\ \text{m}\)
Gabarito
\[ \begin{aligned} b&=\frac{A}{a}=\frac{96}{12}=8\\ P&=2(a+b)=2(12+8)=\boxed{40\ \text{m}}\ (\text{B}) \end{aligned} \]

Para aprofundar: área do quadrado, paralelogramo e triângulo (decomposição de figuras).

Materiais do Matemática Hoje

Relacionadas

Teorema de Pitágoras

Área do Triangulo Equilátero

Teorema de Pitágoras

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube