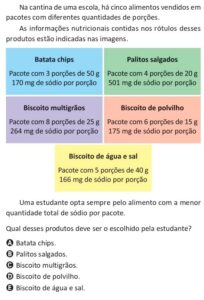
Questão 04. (UEA-AM) A reta \( r \) passa pelos pontos \( (4, 6) \) e \( (0, -4) \) e intersecta o eixo das abscissas no ponto \( P \), conforme mostra a figura.
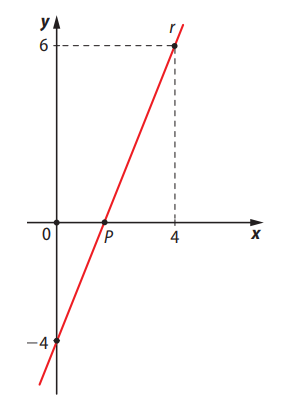
O valor da abscissa do ponto \( P \) é:
- a) \( 2 \)
- b) \( \frac{5}{2} \)
- c) \( \frac{3}{8} \)
- d) \( \frac{8}{5} \)
- e) \( \frac{3}{2} \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A reta passa por dois pontos conhecidos. Desejamos encontrar o ponto \( P \) onde ela cruza o eixo \( x \) (isto é, onde \( y = 0 \)).
1) Encontrar a equação da reta:
Usamos os pontos \( (0, -4) \) e \( (4, 6) \):
Coeficiente angular:
$$ m = \frac{6 – (-4)}{4 – 0} = \frac{10}{4} = \frac{5}{2} $$
Agora, aplicamos na equação geral da reta \( y = mx + b \):
Como passa por \( (0, -4) \), então \( b = -4 \).
Logo, a equação da reta é:
$$ y = \frac{5}{2}x – 4 $$
2) Calcular a abscissa do ponto \( P \):
No ponto \( P \), temos \( y = 0 \). Substituímos:
$$ 0 = \frac{5}{2}x – 4 $$
$$ \frac{5}{2}x = 4 $$
$$ x = \frac{4 \cdot 2}{5} = \frac{8}{5} $$
✅ Conclusão:
- Abscissa do ponto \( P \): $$ \frac{8}{5} $$
- Alternativa correta: d)