Cilindro — Volume, Área Lateral e Área Total (com Exercícios Resolvidos)
Um guia direto para dominar as fórmulas do cilindro, com exemplos passo a passo e lista de exercícios para treinar.
O que é um Cilindro?
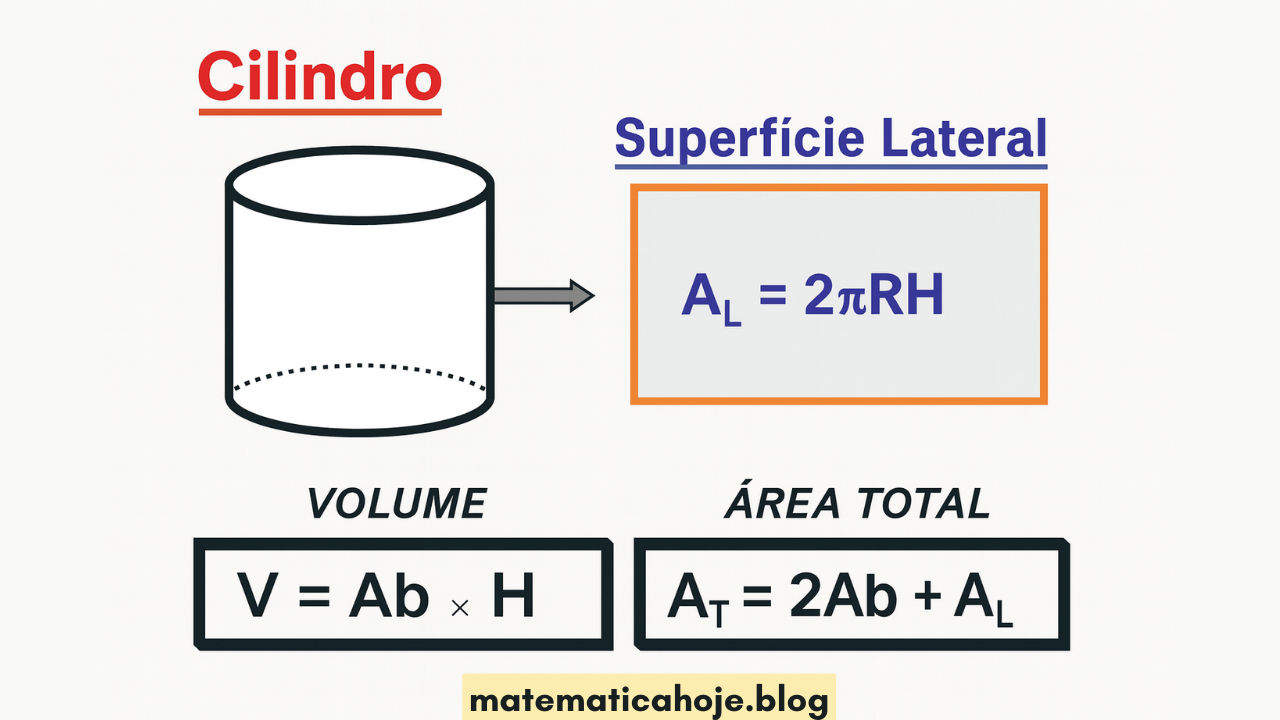
O cilindro é um sólido de revolução formado por duas bases circulares e paralelas, de raio R, unidas por uma superfície lateral retificada de altura H. Em problemas de prova, quase sempre consideramos o cilindro reto (geratriz perpendicular às bases).
Aplicações: latas, tubulações, silos, reservatórios, copos, pistões etc. É conteúdo frequente no ENEM Matemática e concursos.
Fórmulas Essenciais
Áreas
Área da base: \( A_b = \pi R^2 \)
Área lateral: \( A_L = 2\pi R H \)
Área total: \( A_T = 2A_b + A_L = 2\pi R^2 + 2\pi R H = 2\pi R(R+H) \)
Volume
\( V = A_b \cdot H = \pi R^2 \cdot H \)
Dica: desenrole a lateral — ela vira um retângulo de medidas \(2\pi R\) (circunferência) por \(H\).
Reforce com os Mapas Mentais e resolva mais questões no Banco de Questões de Matemática.
Exemplos Resolvidos
Exemplo 1 — Volume
Enunciado. Para um cilindro com \( R = 4 \) cm e \( H = 10 \) cm, calcule o volume.
Ver solução
\( V = \pi R^2 H \)
\( V = \pi \cdot 4^2 \cdot 10 \)
\( V = \pi \cdot 16 \cdot 10 \)
\( V = \mathbf{160\pi\ \text{cm}^3} \) (aprox. \(502.65\ \text{cm}^3\))
Exemplo 2 — Área Total
Enunciado. Um cilindro tem \( R=3 \) cm e \( H=8 \) cm. Determine \( A_T \).
Ver solução
\( A_T = 2\pi R(R+H) \)
\( A_T = 2\pi \cdot 3 \cdot (3+8) \)
\( A_T = 6\pi \cdot 11 \)
\( A_T = \mathbf{66\pi\ \text{cm}^2} \) (aprox. \(207.35\ \text{cm}^2\))
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas (Geometria Espacial, Planimetria, Álgebra, etc.) em um só lugar para revisar antes das provas e concursos.
➡️ Baixar AgoraExercícios Propostos
Resolva e confira o gabarito em cada questão. Para mais listas, acesse o Banco de Questões e a coleção 10 eBooks.
1) Calcule o volume de um cilindro com \( R=5 \) cm e \( H=12 \) cm.
Ver solução
\( V=\pi\cdot5^2\cdot12 \)
\( V=\pi\cdot25\cdot12 \)
\( V=\mathbf{300\pi\ \text{cm}^3} \)
2) (Múltipla escolha) Um cilindro tem \( R=4 \) cm e \( H=9 \) cm. A área lateral é:
- \(24\pi\) cm²
- \(36\pi\) cm²
- \(72\pi\) cm²
- \(90\pi\) cm²
Ver solução
3) Para \( R=3 \) cm e \( H=5 \) cm, determine \( A_T \).
Ver solução
\( A_T=2\pi\cdot3\cdot(3+5) \)
\( A_T=6\pi\cdot8 \)
\( A_T=\mathbf{48\pi\ \text{cm}^2} \)
4) O volume de um cilindro é \( 500\pi\ \text{cm}^3 \) e o raio é \( R=5 \) cm. Encontre \( H \).
Ver solução
\( 500\pi=\pi\cdot25\cdot H \)
\( 500=25H \)
\( H=\mathbf{20\ \text{cm}} \)
5) (Múltipla escolha) Em um cilindro reto, dobrar o raio e manter a altura faz o volume:
- duplicar
- triplicar
- quadruplicar
- ficar inalterado
Ver solução
6) Um rótulo circular cobre exatamente a lateral de uma lata com \( R=3.5 \) cm e \( H=12 \) cm. Qual a área do rótulo?
Ver solução
\( A_L=2\pi\cdot3.5\cdot12 \)
\( A_L=\mathbf{84\pi\ \text{cm}^2} \) (≈ \(263.89\) cm²)
7) Um cilindro tem \( A_L=150\pi \) cm² e \( H=10 \) cm. Determine o raio.
Ver solução
\( 150\pi=2\pi\cdot R\cdot10 \)
\( 150=20R \)
\( R=\mathbf{7.5\ \text{cm}} \)
8) Um reservatório cilíndrico de \( R=1.2 \) m e \( H=2 \) m fica completamente cheio. Quantos litros de água cabem? (\(1\ \text{m}^3=1000\) L)
Ver solução
\( V=\pi\cdot1.2^2\cdot2 \)
\( V=\pi\cdot1.44\cdot2=2.88\pi\ \text{m}^3 \)
\( \approx 9.05\ \text{m}^3 = \mathbf{9050\ \text{L}} \)
9) Um cilindro tem \( A_T=200\pi \) cm² e \( H=5 \) cm. Encontre \( R \).
Ver solução
\( 2R(R+5)=200 \)
\( R(R+5)=100 \)
\( R^2+5R-100=0 \)
\( R=\frac{-5+\sqrt{25+400}}{2}=\frac{-5+\sqrt{425}}{2} \approx \mathbf{8.81\ \text{cm}} \)
10) (Teoria) Ao “desenrolar” a lateral de um cilindro reto, obtemos um retângulo de dimensões:













