O que é uma Circunferência?
Uma circunferência é o conjunto de todos os pontos em um plano que estão a uma distância fixa, chamada de raio, de um ponto fixo chamado de centro. A circunferência é uma das figuras geométricas mais básicas e importantes na matemática, especialmente em geometria e trigonometria.
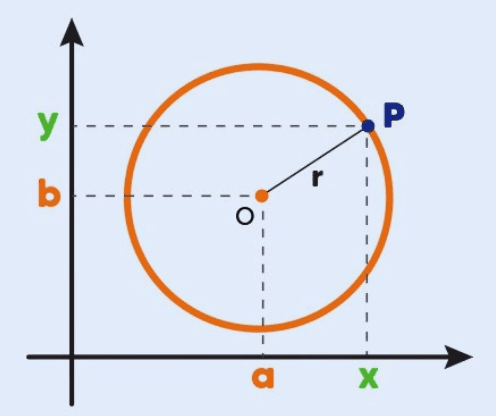
Equação da Circunferência
A equação da circunferência pode ser expressa de duas formas principais: a equação reduzida e a equação geral.
1. Equação Reduzida
A equação reduzida da circunferência é a forma mais simples e direta para descrever uma circunferência no plano cartesiano. Ela é dada pela fórmula:
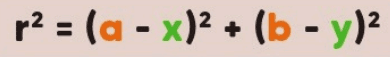
onde:
- (a, b) são as coordenadas do centro da circunferência,
- (x, y) são as coordenadas de um ponto qualquer na circunferência,
- r é o raio da circunferência.
Exemplo: Considere uma circunferência com centro em (3, -2) e raio 5. A equação reduzida será:
(x – 3)2 + (y + 2)2 = 25
Exemplo 1: Determine a equação reduzida da circunferência com centro em (2,−3)(2, -3)(2,−3) e raio 444.
Solução:
- Identifique os valores:
- Centro (a,b)=(2,−3)
- Raio r=4
- Substitua os valores na equação reduzida:
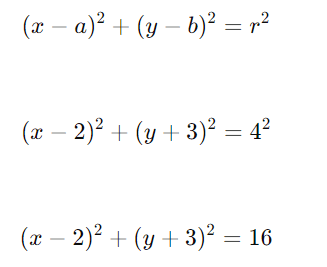
Resposta: A equação reduzida da circunferência é (x−2)2+(y+3)2=16.
Exemplo 2: Encontre a equação reduzida da circunferência com centro em (−1,4)(-1, 4)(−1,4) e raio 777.
Solução:
- Identifique os valores:
- Centro (a,b)=(−1,4)
- Raio r=7
- Substitua os valores na equação reduzida:
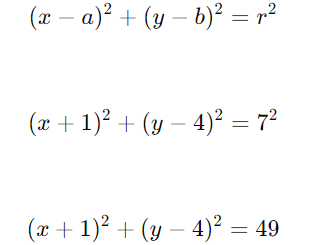
Resposta: A equação reduzida da circunferência é (x+1)2+(y−4)2=49.
Exemplo 3: Determine o raio da circunferência dada pela equação reduzida (x−5)2+(y+2)2=36.
Solução: Compare com a fórmula geral da equação reduzida
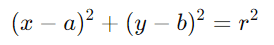
Aqui, r2 é o termo constante na equação.
Na equação dada, r2=36.
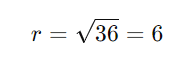
Resposta: O raio da circunferência é 6.
Exemplo 4: Encontre a coordenada x do ponto na circunferência dada pela equação reduzida (x−1)2+(y−3)2=25, sabendo que a coordenada y do ponto é 5.
Substitua y na equação da circunferência:
- A equação da circunferência é (x−1)2+(y−3)2=25.
- Substitua y=5 na equação:
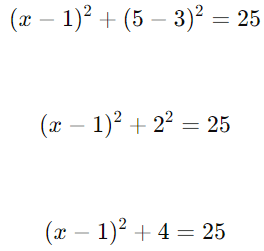
Resolva a equação para encontrar x:
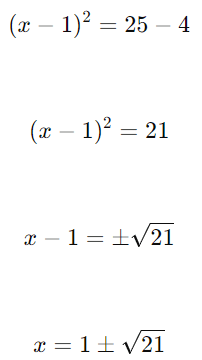
Resposta: As coordenadas x dos pontos na circunferência onde y=5 são
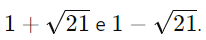
2. Equação Geral
A equação geral da circunferência é uma forma mais expandida da equação da circunferência. Ela é expressa como:

onde:
- (a, b) são as coordenadas do centro da circunferência, e
- r é o raio da circunferência.
Exemplo: A equação geral x2 + y2 – 6x – 8y + 9 = 0 pode ser transformada na equação reduzida da seguinte forma:
- Completar o quadrado para x e y:
- x2 – 6x + y2 – 8y = -9
(x – 3)2 – 9 + (y – 4)2 – 16 = -9
(x – 3)2 + (y – 4)2 = 16
Assim, a equação reduzida é (x – 3)2 + (y – 4)2 = 16, com centro (3, 4) e raio 4.
Propriedades da Circunferência
- Comprimento da Circunferência: A fórmula para calcular o comprimento de uma circunferência é dada por 2πr, onde r é o raio.
- Área da Circunferência: A área de uma circunferência é calculada por πr2.
Aplicações da Circunferência
As circunferências são amplamente utilizadas em diversas áreas, como engenharia, arquitetura, design e até na vida cotidiana. Elas são essenciais para entender conceitos mais avançados em geometria e trigonometria, e suas propriedades são fundamentais em cálculos de áreas e perímetros.
Conclusão
Entender as equações da circunferência e suas propriedades é crucial para a resolução de problemas em geometria. A equação reduzida fornece uma maneira direta e prática de descrever circunferências, enquanto a equação geral oferece uma forma mais versátil para manipulações algébricas e análise.
Esperamos que este guia tenha fornecido uma visão clara e compreensiva sobre circunferências. Se tiver mais perguntas ou precisar de mais exemplos, sinta-se à vontade para explorar mais!
Leia também
Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade
Distância entre Retas e Cálculo da Área de um Triângulo
Circunferência: Equação Geral e Reduzida
A Parábola: Definição, Propriedades e Equações
Elipse: Conceito, Propriedades e Equações













