Coeficiente Linear — O ponto onde a reta corta o eixo Y
O coeficiente linear é um dos elementos fundamentais da equação da reta. Ele representa o ponto em que a reta cruza o eixo vertical \( Y \) no plano cartesiano.
📘 O que é o Coeficiente Linear
Na equação da reta expressa na forma reduzida:
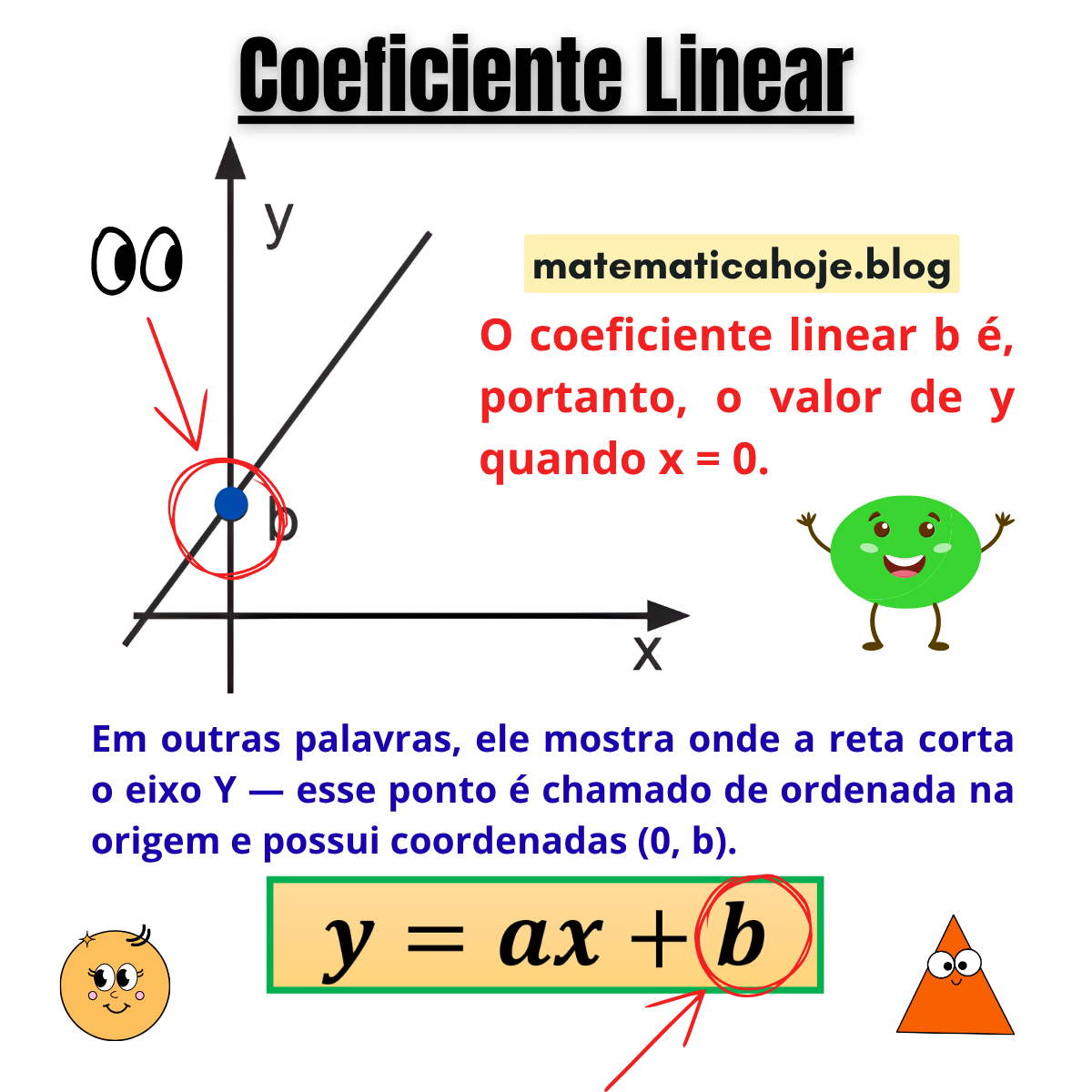
O valor \( b \) é chamado de coeficiente linear. Ele indica o valor de \( y \) quando \( x = 0 \). Em outras palavras, é o ponto onde a reta corta o eixo \( Y \), chamado de ordenada na origem.
🧮 Interpretação Geométrica
No plano cartesiano, toda reta pode ser representada por \( y = ax + b \), onde:
- \( a \) → coeficiente angular (indica a inclinação da reta);
- \( b \) → coeficiente linear (indica onde a reta cruza o eixo Y).
O ponto de interseção tem coordenadas \( (0, b) \). Se \( b \) for positivo, a reta corta o eixo Y acima da origem; se for negativo, corta abaixo.
📐 Exemplo 1
Exemplo: Considere a reta \( y = 2x + 3 \).
O coeficiente linear é \( b = 3 \), o que significa que a reta corta o eixo Y no ponto \( (0, 3) \).
📐 Exemplo 2
Exemplo: Para a reta \( y = -x – 4 \):
O coeficiente linear é \( b = -4 \), ou seja, a reta corta o eixo Y no ponto \( (0, -4) \).
📚 Exercícios de Fixação
1. Determine o coeficiente linear da reta \( y = 5x – 2 \).
2. Qual é o ponto de interseção com o eixo Y da reta \( y = -3x + 7 \)?
3. (Desafio) Encontre o coeficiente linear da reta que passa por \( (2, 5) \) e tem coeficiente angular \( a = 3 \).