Se você está estudando análise combinatória e já ouviu falar em combinação com repetição, mas não sabe por onde começar, este artigo é para você. Vamos explicar o conceito de forma simples, mostrar a fórmula, resolver exemplos práticos e esclarecer onde esse tipo de combinação é usado. Prepare-se para dominar esse tema!
O que é Combinação com Repetição?
A combinação com repetição, também conhecida como combinação composta, é um tipo de agrupamento na análise combinatória onde os elementos de um conjunto podem ser escolhidos mais de uma vez, e a ordem das escolhas não importa.
Isso significa que, se você tiver um conjunto de nn elementos e quiser formar grupos de kk elementos, permitindo que um mesmo elemento seja repetido no grupo, estamos falando de combinação com repetição.
Por exemplo: Se você tem as frutas {maçã, banana, laranja} e quer escolher 3 frutas, é possível selecionar algo como:
- {maçã, maçã, banana}
- {maçã, laranja, laranja}
Aqui, repetimos elementos no mesmo grupo, e isso caracteriza uma combinação com repetição.
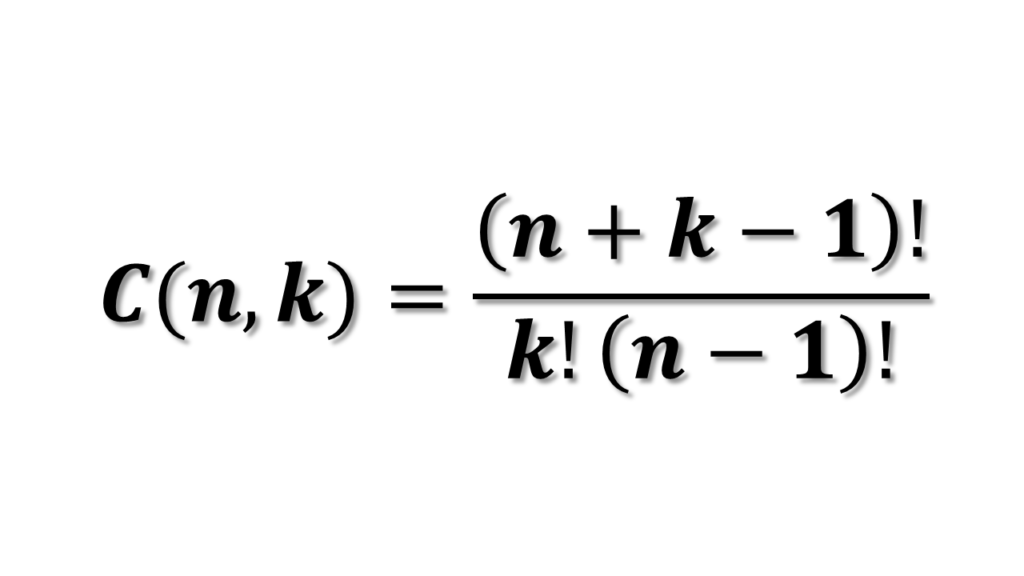
A Fórmula da Combinação com Repetição
A fórmula para calcular o número de combinações com repetição é:
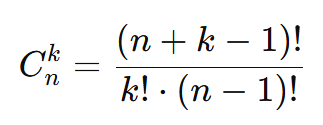
Onde:
- n: número total de elementos no conjunto original.
- k: número de elementos que você quer escolher.
- n + k – 1: ajuste para permitir repetições.
- k!: fatorial do número de elementos escolhidos.
- (n – 1)!: fatorial do número de elementos originais, ajustado para repetição.
Essa fórmula é derivada de uma ideia chamada “princípio das combinações com repetição”, que considera as escolhas repetidas como diferentes do ponto de vista matemático.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉 Leia o artigo completo aqui!
Exemplo 1: Combinação com Repetição na Prática
Imagine que você tem um conjunto de n = 3 frutas: {maçã, banana, laranja}, e quer escolher k = 2 frutas, permitindo repetições.
Passo 1: Aplicar a Fórmula
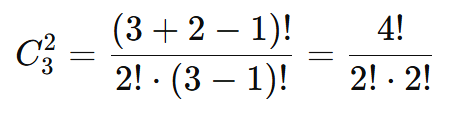
Substituímos na fórmula:
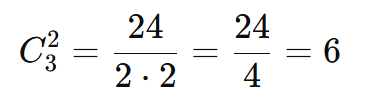
Passo 2: Interpretar o Resultado Existem 6 combinações possíveis:
- {maçã, maçã}
- {maçã, banana}
- {maçã, laranja}
- {banana, banana}
- {banana, laranja}
- {laranja, laranja}
Exemplo 2: Distribuindo Itens com Repetição
Um problema clássico é a distribuição de itens. Suponha que você tem 4 moedas para distribuir em 3 caixas, permitindo que uma mesma caixa receba mais de uma moeda.
Aqui, o número de combinações com repetição será:
Passo 1: Identificar n e k
- n = 3: número de caixas.
- k = 4: número de moedas.
Passo 2: Aplicar a Fórmula
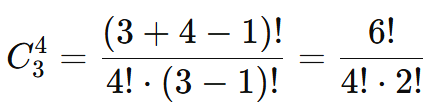
Substituímos na fórmula:
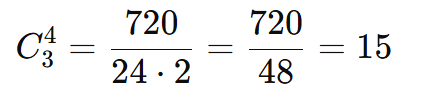
Passo 3: Interpretar o Resultado Existem 15 formas distintas de distribuir as moedas nas caixas.
Baixe o e-book gratuito Formulas Matemática
Quando Usar a Combinação com Repetição?
A combinação com repetição é útil em situações como:
- Escolher itens repetidos (como frutas, moedas ou objetos).
- Distribuir recursos entre grupos, permitindo que um grupo receba mais de um recurso.
- Resolver problemas de partição de inteiros, como dividir um número em somas.
Dica para Lembrar: A Diferença entre Arranjo e Combinação
- No arranjo com repetição, a ordem importa. Exemplo: AB ≠ BA
- Na combinação com repetição, a ordem não importa. Exemplo: AB=BA
O que é Combinação? Combinação é um conceito da análise combinatória que representa o número de maneiras de selecionar k elementos de um conjunto com n elementos distintos, sem levar em conta a ordem dos elementos escolhidos. Ou seja, na combinação, a ordem dos elementos não altera o resultado.
Resumo Final
A combinação com repetição é um conceito poderoso que permite resolver problemas onde os elementos podem se repetir e a ordem não importa. Ela é amplamente usada em matemática e na vida cotidiana, como na organização de recursos ou na escolha de itens.
Fórmula Importante:
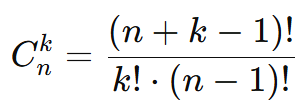
Pratique e Domine!
Agora é sua vez! Tente resolver este problema:
Questão: Um restaurante tem 5 tipos de sobremesas. Quantas formas diferentes existem de escolher 4 sobremesas, permitindo repetições?
(Se precisar de ajuda, volte aqui e confira os passos para resolver!)
Compreender combinação com repetição é essencial para se destacar em análise combinatória. Continue praticando e você dominará o assunto em pouco tempo! 🚀

























