Comprimento da Circunferência

Comprimento da Circunferência — fórmulas, exemplos e exercícios

Comprimento da Circunferência

O comprimento da circunferência (também chamado de perímetro do círculo) é a medida total da sua borda. As fórmulas principais são \(C=2\pi r\) e \(C=\pi d\).

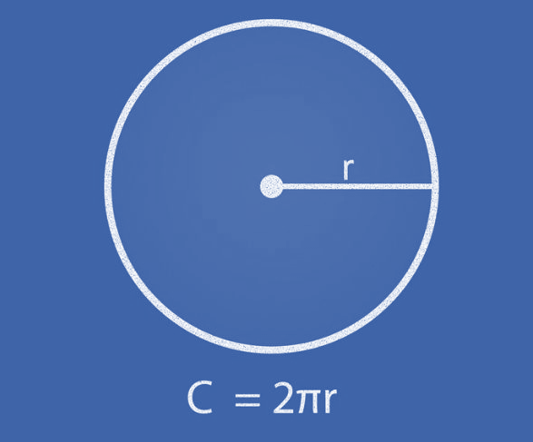
Circunferência com raio r e diâmetro d
Se \(r\) é o raio e \(d=2r\) é o diâmetro, então \(C=2\pi r=\pi d\).
Estude em conjunto: Área do Círculo, Área do Setor Circular, Lei dos Senos e Polígonos Regulares.

Fórmulas (empilhadas e destacadas)

\[ \textbf{1) Por raio:}\quad \boxed{C=2\pi r} \]
\[ \textbf{2) Por diâmetro }(d=2r):\quad \boxed{C=\pi d} \]
\[ \textbf{3) Arco de circunferência em graus }(\alpha):\quad \boxed{L=\frac{\alpha}{360^\circ}\,2\pi r} \]
\[ \textbf{4) Arco em radianos }(\theta):\quad \boxed{L=r\theta} \]

As fórmulas de arco (3 e 4) são equivalentes porque \(\theta=\dfrac{2\pi\alpha}{360^\circ}\).

Quadro-resumo (para imprimir)

Fórmulas principais de comprimento da circunferência e arco:

\[ \textbf{Circunferência (por raio):}\quad \boxed{C=2\pi r} \]
\[ \textbf{Circunferência (por diâmetro):}\quad \boxed{C=\pi d}\quad (d=2r) \]
\[ \textbf{Arco (ângulo em graus }\alpha\text{):}\quad \boxed{L=\frac{\alpha}{360^\circ}\,2\pi r} \]
\[ \textbf{Arco (ângulo em radianos }\theta\text{):}\quad \boxed{L=r\theta} \]
\[ \text{Conversão:}\quad \theta=\frac{\pi}{180^\circ}\,\alpha \]

Dica: use \(C=2\pi r\) quando o dado for o raio; \(C=\pi d\) quando tiver o diâmetro; para arcos, escolha diretamente a fórmula no mesmo sistema do ângulo (graus ou radianos).

Exemplos resolvidos (situação-problema)

1

Pneu de bicicleta — raio conhecido

O modelo reduzido de um pneu tem raio \(r=0{,}35\,\text{m}\).

Dados
\(r=0{,}35\,\text{m}\).

Qual é o comprimento dessa circunferência?

Ver solução
\[ \begin{aligned} C&=2\pi r\\ &=2\pi\cdot 0{,}35\\ &=0{,}70\pi\\ &\approx \boxed{2{,}199\ \text{m}} \end{aligned} \]
2

Pista circular — diâmetro informado

Uma pista circular tem diâmetro \(d=1{,}2\,\text{km}\).

Dados
\(d=1{,}2\,\text{km}\).

Qual é o comprimento da pista?

Ver solução
\[ \begin{aligned} C&=\pi d\\ &=\pi\cdot 1{,}2\\ &\approx \boxed{3{,}770\ \text{km}} \end{aligned} \]
3

Descobrindo o raio pelo perímetro

Uma fonte circular foi medida ao redor e resultou em \(C=62{,}8\,\text{m}\).

Dados
\(C=62{,}8\,\text{m}\).

Qual é o raio da fonte?

Ver solução
\[ \begin{aligned} C&=2\pi r \Rightarrow r=\frac{C}{2\pi}\\ r&=\frac{62{,}8}{2\pi}=\frac{62{,}8}{6{,}28318\ldots}\\ &\approx \boxed{10\ \text{m}} \end{aligned} \]
4

Arco em graus

Em um mostrador, o ponteiro percorre um arco de \(\alpha=54^\circ\) no círculo de raio \(r=10\,\text{cm}\).

Dados
\(r=10\,\text{cm}\), \(\alpha=54^\circ\).

Qual é o comprimento do arco?

Ver solução
\[ \begin{aligned} L&=\frac{\alpha}{360^\circ}\,2\pi r\\ &=\frac{54^\circ}{360^\circ}\cdot 2\pi\cdot 10\\ &=\frac{3}{20}\cdot 20\pi\\ &=3\pi\\ &\approx \boxed{9{,}425\ \text{cm}} \end{aligned} \]

Erros comuns (e como evitar)

  • Trocar raio por diâmetro. Se o enunciado der \(d\), use \(C=\pi d\); se der \(r\), use \(C=2\pi r\).
  • Confundir graus e radianos. Em graus: \(L=\dfrac{\alpha}{360^\circ}2\pi r\). Em radianos: \(L=r\theta\).
  • Unidades. Converta antes de calcular (cm ↔ m ↔ km), depois arredonde.

Para aplicações com área, veja área do círculo e área do setor circular.

Exercícios (múltipla escolha)

1

Circunferência por raio

Um prato tem raio \(r=9\,\text{cm}\).

O comprimento da borda é:

  • A) \(36\ \text{cm}\)
  • B) \(18\pi\ \text{cm}\ (\approx 56{,}55)\)
  • C) \(9\pi\ \text{cm}\)
  • D) \(27\pi\ \text{cm}\)
Gabarito
\[ C=2\pi r=2\pi\cdot 9=\boxed{18\pi\ \text{cm}}\ (\text{B}) \]
2

Circunferência por diâmetro

Uma tampa circular tem diâmetro \(d=14\,\text{cm}\).

Seu comprimento é:

  • A) \(28\ \text{cm}\)
  • B) \(7\pi\ \text{cm}\)
  • C) \(14\pi\ \text{cm}\ (\approx 43{,}98)\)
  • D) \(21\pi\ \text{cm}\)
Gabarito
\[ C=\pi d=\pi\cdot 14=\boxed{14\pi\ \text{cm}}\ (\text{C}) \]
3

Encontrando o raio

Uma mesa circular possui comprimento de borda \(C=31{,}4\,\text{cm}\).

O raio da mesa é aproximadamente:

  • A) \(3{,}0\ \text{cm}\)
  • B) \(4{,}0\ \text{cm}\)
  • C) \(5{,}0\ \text{cm}\)
  • D) \(6{,}0\ \text{cm}\)
Gabarito
\[ r=\frac{C}{2\pi}=\frac{31{,}4}{6{,}28318\ldots}\approx \boxed{5{,}0\ \text{cm}}\ (\text{C}) \]
4

Arco em radianos

Um guindaste gira um cabo descrevendo arco com raio \(r=12\,\text{m}\) e ângulo \(\theta=1{,}3\ \text{rad}\).

O comprimento do arco percorrido é:

  • A) \(12{,}0\ \text{m}\)
  • B) \(13{,}0\ \text{m}\)
  • C) \( \mathbf{15{,}6\ \text{m}} \)
  • D) \(18{,}0\ \text{m}\)
Gabarito
\[ L=r\theta=12\cdot 1{,}3=\boxed{15{,}6\ \text{m}}\ (\text{C}) \]

Quer ir além? Confira área do círculo, área do setor e o nosso banco de questões.

Materiais do Matemática Hoje

Relacionadas

Relação Fundamental do Triângulo Retângulo

Ângulos Congruentes

Coroa Circular

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube