Concurso dos Correios: 10 Questões de Matemática Essenciais para Passar

Vamos resolver o problema comparando os montantes obtidos em juros compostos e em juros simples.

1. Cálculo do montante com juros compostos:

Sabemos que o investidor aplicou R$ 10.000,00 por 2 anos a uma taxa de 10% ao ano. A fórmula do montante em juros compostos é:

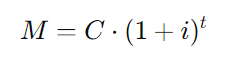
Onde:

• ( M ) é o montante,
• ( C ) é o capital inicial (R$ 10.000,00),
• ( i ) é a taxa de juros (10% ou 0,10),
• ( t ) é o tempo de aplicação (2 anos).

Substituindo os valores:

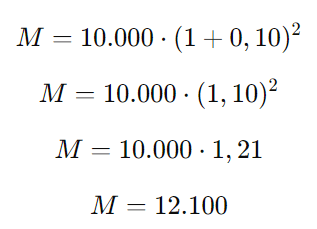
O montante obtido em juros compostos é R$ 12.100,00.

2. Cálculo da taxa de juros simples:

Agora, queremos encontrar a taxa de juros simples que, aplicada sobre o mesmo capital (R$ 10.000,00) por 3 anos, resultaria no mesmo montante de R$ 12.100,00.

A fórmula do montante em juros simples é:

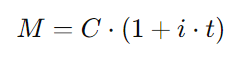
Substituindo o montante ( M = 12.100 ), o capital ( C = 10.000 ), e o tempo ( t = 3 ) anos, temos:

A taxa de juros simples necessária seria 7% ao ano.

Resposta correta: A) 7%.

Vamos resolver a questão calculando o juro obtido no investimento utilizando a fórmula dos juros compostos.

1. Cálculo do montante:

A fórmula para o montante em juros compostos é:

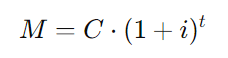
Onde:

• ( M ) é o montante,
• ( C ) é o capital inicial (R$ 10.000,00),
• ( i ) é a taxa de juros (10% ou 0,10),
• ( t ) é o tempo de aplicação (2 anos).

Substituindo os valores:

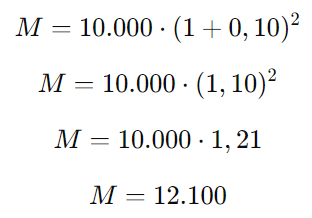
O montante ao final de 2 anos é R$ 12.100,00.

2. Cálculo dos juros:

Agora, calculamos o juro total, que é a diferença entre o montante e o capital inicial:

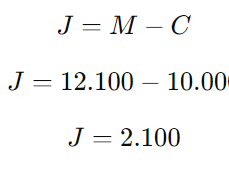
3. Análise das alternativas:

O juro obtido foi de R$ 2.100,00, que é superior a R$ 1.900,00 e inferior a R$ 2.200,00.

Resposta correta: C) superior a R$ 1.900,00 e inferior a R$ 2.200,00.

Vamos resolver essa questão calculando o dia da semana em que o funcionário voltará ao trabalho após 180 dias de afastamento, começando em uma quarta-feira.

Passo 1: Saber que o ciclo semanal se repete a cada 7 dias

Se o funcionário foi afastado por 180 dias, precisamos determinar em que dia da semana ele retornará após esse período. Para isso, usamos o resto da divisão de 180 por 7, já que 7 dias formam uma semana completa.

Passo 2: Fazer a divisão de 180 por 7

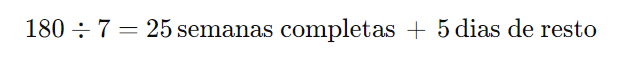
Isso significa que, após 25 semanas (que terminam em uma quarta-feira), restam 5 dias a serem contados a partir da quarta-feira.

Passo 3: Contar os dias a partir de quarta-feira

• Quarta-feira + 1 dia = quinta-feira
• Quinta-feira + 1 dia = sexta-feira
• Sexta-feira + 1 dia = sábado
• Sábado + 1 dia = domingo
• Domingo + 1 dia = segunda-feira

Portanto, o funcionário retornará ao trabalho em uma segunda-feira.

Passo 4: Exame médico no primeiro dia útil

Se o funcionário retorna em uma segunda-feira, que é um dia útil, o exame médico será realizado nesse mesmo dia.

Resposta:

O exame será realizado em uma segunda-feira.

A resposta correta é C) segunda-feira.

Para resolver a questão, vamos calcular a distância total percorrida por Nelson, em metros, a partir dos pontos da estrada fornecidos.

Passo 1: Calcular a distância da ida

Nelson partiu do quilômetro 321 e foi até a cidade que está no quilômetro 620. A distância percorrida na ida é:

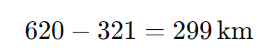
Passo 2: Calcular a distância da volta

Nelson voltou da cidade no quilômetro 620 até a fazenda que fica no quilômetro 452. A distância percorrida na volta é:

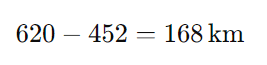
Passo 3: Calcular a distância total em quilômetros

A distância total percorrida é a soma das distâncias da ida e da volta:

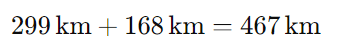
Passo 4: Converter a distância para metros

Sabemos que 1 km = 1.000 metros. Portanto, a distância total percorrida em metros é:

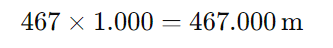
Resposta:

Nelson percorreu 467.000 metros.

A resposta correta é B) 467.000 m.

Vamos chamar de ( x ) o número de pessoas na primeira sala e de ( y ) o número de pessoas na segunda sala.

Sabemos que:

A capacidade de cada sala é de 300 pessoas.

Na primeira sala, 3/5 da capacidade estavam ocupados, então o número de pessoas na primeira sala é:

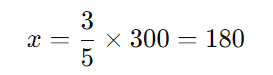
Na segunda sala, havia metade do número de pessoas da primeira sala, ou seja:

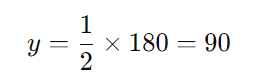
Agora, para saber o total de pessoas no cinema, somamos ( x ) e ( y ):

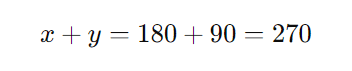
Portanto, o número total de pessoas no cinema nesse dia era 270.

A resposta correta é a letra B).

Essa questão envolve o conceito de trabalho inversamente proporcional. Quando mais pessoas fazem o mesmo trabalho, o tempo necessário para completá-lo diminui proporcionalmente.

Vamos resolver o problema utilizando regra de três.

Sabemos que:

• 1 carteiro entrega a quantidade de correspondências em 8 horas.
• Queremos saber quanto tempo 6 carteiros levarão para entregar a mesma quantidade de correspondências.

A relação entre o número de carteiros e o tempo é inversamente proporcional, ou seja, quanto mais carteiros, menos tempo eles levarão. Montamos a regra de três inversa:

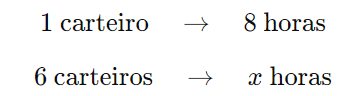
Como é uma relação inversa, multiplicamos em “cruz”:

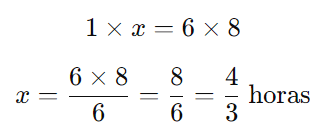
Agora, convertendo 4/3 horas para horas e minutos:

Sabemos que 1/3 de hora = 20 minutos.

Portanto, o tempo que 6 carteiros levarão para entregar a mesma quantidade de correspondências é 1 hora e 20 minutos.

A resposta correta é D) 1 h e 20 min.

Vamos resolver o problema utilizando a regra de três.

Sabemos que:

• 20 gotas correspondem a 1 mL.
• Queremos saber quantos mililitros correspondem a 3.456.000 gotas.
• Que é a quantidade de gotas em 30 dias (30*24*60)

Montamos a regra de três:

Agora, multiplicamos cruzado:

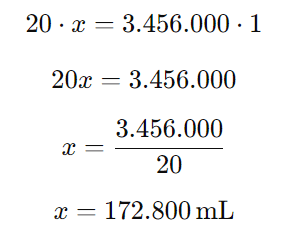
Agora, convertendo para litros:

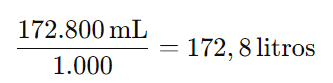
Portanto, o desperdício é 172,8 litros, confirmando que a resposta correta é A) 172,8.

Para resolver o problema, devemos usar a fórmula do termo geral da sequência dada:

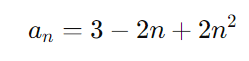
Vamos calcular os 5 primeiros termos da sequência, substituindo (n = 1, 2, 3, 4, 5) na fórmula.

Cálculo dos termos:

1. Para (n = 1):
   a1 = 3 – 2(1) + 2(1)² = 3 – 2 + 2 = 3
2. Para (n = 2):
   a2 = 3 – 2(2) + 2(2)² = 3 – 4 + 8 = 7
3. Para (n = 3):
   a3 = 3 – 2(3) + 2(3)² = 3 – 6 + 18 = 15
4. Para (n = 4):
   a4 = 3 – 2(4) + 2(4)² = 3 – 8 + 32 = 27
5. Para (n = 5):
   a5 = 3 – 2(5) + 2(5)² = 3 – 10 + 50 = 43

Soma dos 5 primeiros termos:

Agora, somamos os valores calculados:
S = a1 + a2 + a3 + a4 + a5 = 3 + 7 + 15 + 27 + 43 = 95

Resposta:

A soma dos primeiros 5 números dessa sequência é igual a 95, logo a alternativa correta é a B.

Chamaremos de A, B e C as quantidades de notas de R$10, R$5 e R$1, respectivamente, que Luís Alberto utilizou para efetuar o pagamento.

Portanto, o valor total pago por ele pode ser representado pela expressão

10A + 5B + 1C = 101

O enunciado diz que a quantidade total de notas é 20, ou seja

A + B + C = 20

Resumindo:

1.    10A + 5B + 1C = 101
2.    A + B + C = 20

Isolando C na segunda equação, temos

C = 20 – A – B

Substituindo na primeira,

10A + 5B + (20 – A – B) = 101

10A – A + 5B – B = 101 – 20

9A + 4B = 81

Temos uma relação entre as quantidades de notas de R$10 e de R$5. A questão pergunta sobre as notas de R$5, logo, vamos isolar B:

4B = 81 – 9A

B = (81 – 9A) / 4

Devemos nos lembrar que A e B devem ser números inteiros (pois representam quantidades) e que A deve assumir o maior valor possível que satisfaça as demais condições.

 – Para que B seja um inteiro, o resultado de (81 – 9A) deve ser um múltiplo de 4 e, portanto, um número par. 

 – Para que (81 – 9A) seja par, é necessário que 9A seja ímpar (ímpar – ímpar = par). 

 – Para que 9A seja ímpar, é necessário que A seja ímpar.

Logo, A é um número ímpar.

Assim, veremos quais o valores que A pode assumir, do maior pro menor. O primeiro que satisfazer todas as condições, será o número que procuramos.

• A deve ser menor que 10:

Se A fosse 10, então teríamos, no mínimo, R$106, pois deve haver pelo menos uma nota de R$5 e pelo menos uma de R$1.

Assim, teríamos 

(10 * 10) + 5 + 1 = 106

O que excederia o valor de R$101.

Restam então os valores 9, 7, 5, 3 e 1.

• Se A fosse 9:

B = (81 – 9*9) / 4

B = (81 – 81) / 4

B = 0 / 4

B = 0

B não pode ser 0, pois tem que haver pelo menos uma nota de cada. Logo, A não pode ser 9.

• Se A fosse 7;

B = (81 – 9*7) / 4

B = (81 – 63) / 4

B = 18 / 4

B = 4,5

B deve ser um inteiro, logo, A não pode ser 7.

• Se A fosse 5:

B = (81 – 9*5) / 4

B = (81 – 45) / 4

B = 36 / 4

B = 9

Encontramos os valores que procurávamos:

A = 5

B = 9

B é 9, que é uma potência de 3 (9 = 3²).

Logo, a alternativa C está correta.

Vamos chamar os pesos de Carlos, Renata e Jerry de ( C ), ( R ) e ( J ), respectivamente.

Temos as seguintes equações com base nas pesagens:

1. ( C + J = 87 ) (Carlos e Jerry juntos)
2. ( C + R = 123 ) (Carlos e Renata juntos)
3. ( R + J = 66 ) (Renata e Jerry juntos)

Agora, vamos resolver esse sistema de equações.

Passo 1: Isolando ( C ) na equação ( C + J = 87 )

C = 87 – J

Passo 2: Substituindo ( C ) na equação ( C + R = 123 )

(87 – J) + R = 123

87 + R – J = 123

R – J = 123 – 87

R – J = 36

R = J + 36

Passo 3: Substituindo ( R ) na equação ( R + J = 66 )

(J + 36) + J = 66

2J + 36 = 66

2J = 66 – 36

2J = 30

J = 30/2

J = 15

O cachorro Jerry pesa 15 kg.

A resposta correta é a letra D).