Cone Reto e Cone Oblíquo
O cone é um sólido geométrico fundamental da geometria espacial. Ele pode ser classificado em reto ou oblíquo de acordo com a posição de seu eixo em relação à base.
1) Definição de cone
O cone é um sólido formado pela rotação de um triângulo retângulo em torno de um de seus catetos (no caso do cone reto) ou pela união de todos os segmentos de reta que ligam um ponto fixo \(V\) (vértice) a todos os pontos de uma circunferência da base.
- Base: círculo de raio \(r\).
- Altura (h): distância perpendicular do vértice ao plano da base.
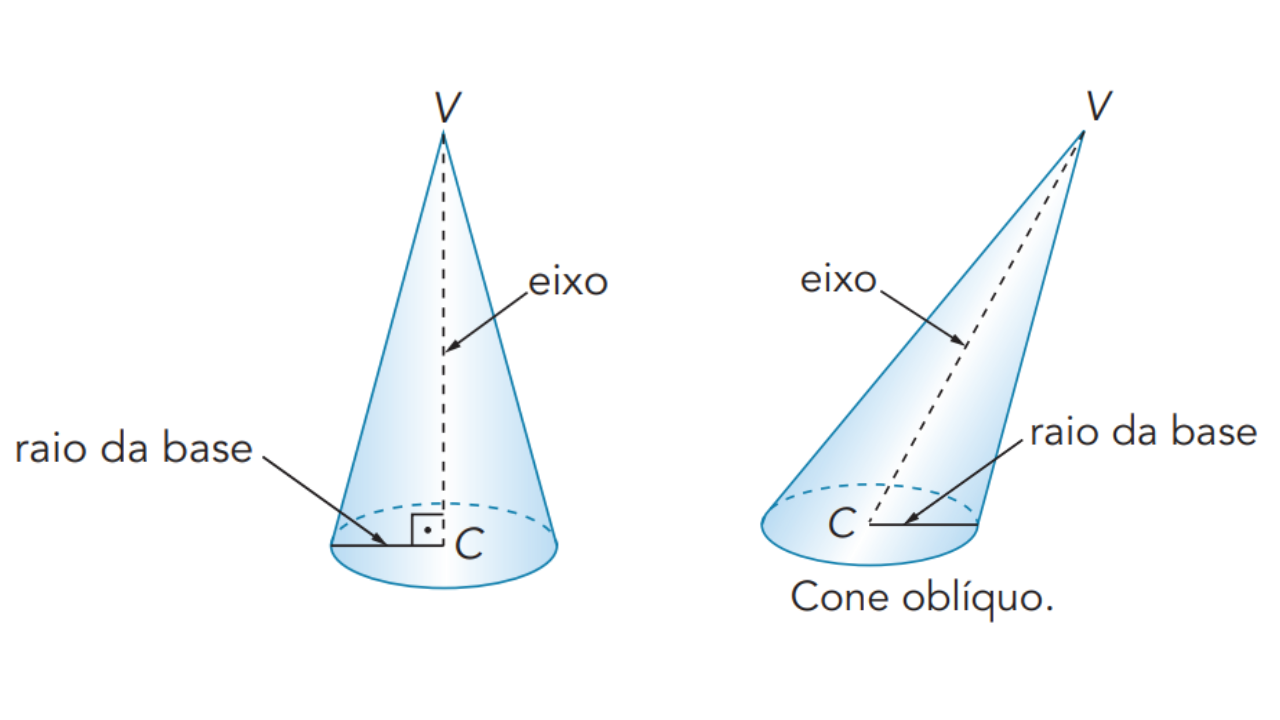
- Eixo: segmento que liga o vértice ao centro da base.
- Geratriz (g): segmento que une o vértice a um ponto qualquer da circunferência da base.
2) Cone Reto
No cone reto, o eixo coincide com a altura, ou seja, é perpendicular à base. A projeção do vértice sobre o plano da base coincide com o centro da circunferência.
- Eixo ⟂ base
- Triângulo gerador é isósceles
- Fórmulas de área e volume clássicas
3) Cone Oblíquo
No cone oblíquo, o vértice não está alinhado com o centro da base, ou seja, o eixo não é perpendicular à base. Ele é inclinado, e por isso as geratrizes não têm o mesmo comprimento.
- Eixo inclinado em relação à base
- Não há uma única geratriz: os comprimentos variam
- Volume pode ser calculado pela mesma fórmula do cone reto
4) Fórmulas principais (cone reto)
Área da base:
Área lateral:
Área total:
Volume:
Para o cone oblíquo, a fórmula do volume é a mesma, mas a área lateral exige métodos específicos, como a decomposição em integrais ou aproximações geométricas.
5) Exemplo resolvido
Exemplo: Um cone reto tem raio \(r=5\) cm, altura \(h=12\) cm. Calcule a área total e o volume.
Mostrar solução
1. Calcular a geratriz: \(g=\sqrt{r^2+h^2}=\sqrt{25+144}=\sqrt{169}=13\).
2. Área lateral: \(A_l=\pi r g=\pi\cdot5\cdot13=65\pi\).
3. Área total: \(A_t=A_l+A_b=65\pi+25\pi=90\pi\; \text{cm}^2\).
4. Volume: \(V=\frac{1}{3}\pi r^2 h=\frac{1}{3}\pi\cdot25\cdot12=100\pi\; \text{cm}^3\).
6) Exercícios para praticar
1. Um cone reto tem \(r=3\) cm e \(h=4\) cm. Calcule o volume.
Ver solução
\(V=\tfrac{1}{3}\pi r^2 h=\tfrac{1}{3}\pi\cdot9\cdot4=12\pi\;\text{cm}^3\).
2. Num cone reto, \(r=6\) cm e \(g=10\) cm. Determine a área lateral.
Ver solução
\(A_l=\pi r g=\pi\cdot6\cdot10=60\pi\;\text{cm}^2\).
7) Links relacionados
Curiosidade: cones oblíquos são muito utilizados em arquitetura, como em torres inclinadas e cúpulas decorativas.






















