Cone — Volume, Geratriz, Área Lateral e Área Total (com Exercícios Resolvidos)

Tudo o que você precisa para dominar cones: fórmulas, relações métricas, exemplos passo a passo e uma lista de exercícios para treinar.

O que é um Cone?

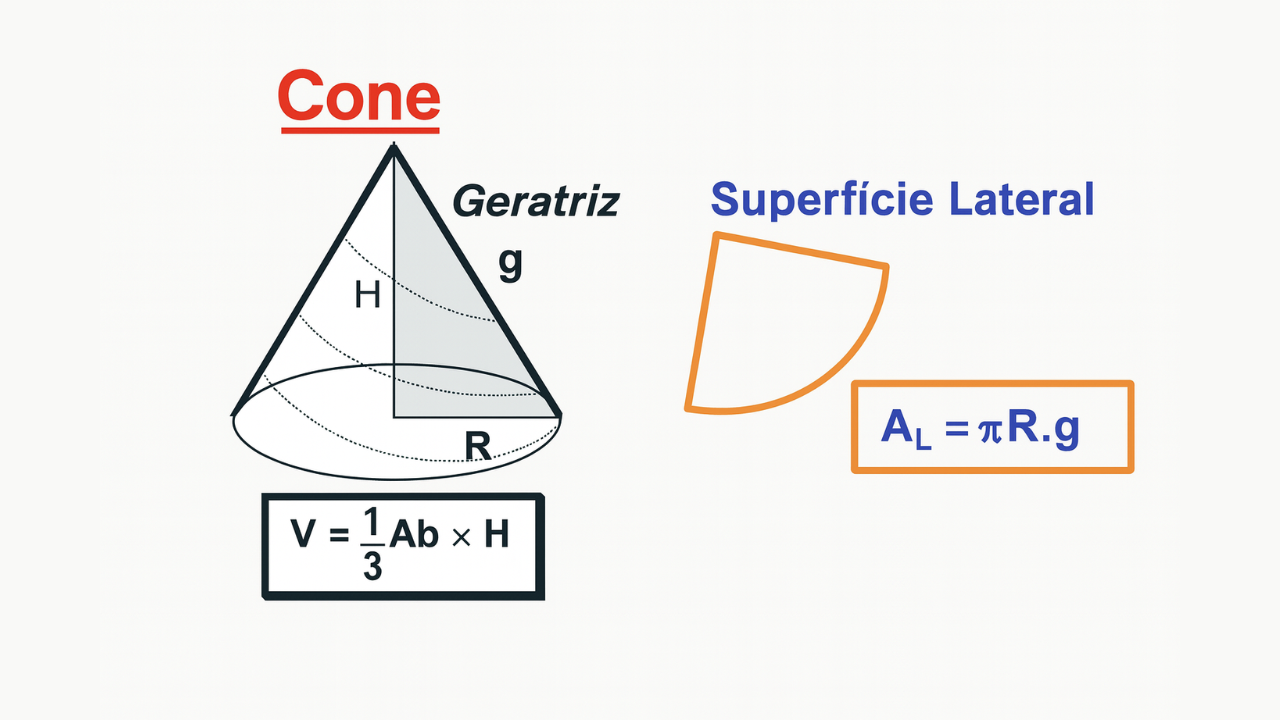
O cone reto é um sólido de revolução obtido ao girar um triângulo retângulo em torno de um de seus catetos. Possui duas medidas principais:

R: raio da base (círculo);
H: altura do cone;
g: geratriz (hipotenusa do triângulo gerador).

Relação métrica no cone reto: \( g^2 = R^2 + H^2 \).

Ao “desenrolar” a superfície lateral, obtemos um setor circular de raio \(g\) e arco igual à circunferência da base (\(2\pi R\)).

Fórmulas Essenciais

Volume

\( V = \dfrac{1}{3}\,A_b \cdot H = \dfrac{1}{3}\,\pi R^2 H \)

Áreas

Área da base: \( A_b = \pi R^2 \)
Área lateral: \( A_L = \pi R g \)
Área total: \( A_T = A_b + A_L = \pi R^2 + \pi R g \)

Como obter \(A_L\): a área do setor é \( \frac{\theta}{2\pi}\cdot \pi g^2 \) com \( g\theta = 2\pi R \Rightarrow A_L = \pi R g \).

Reforce com os Mapas Mentais e pratique no Banco de Questões.

Exemplos Resolvidos

Exemplo 1 — Volume do Cone

Enunciado. Para um cone com \( R=4 \) cm e \( H=9 \) cm, calcule o volume.

Ver solução

\( V=\frac{1}{3}\pi R^2 H \)
\( V=\frac{1}{3}\pi\cdot4^2\cdot9 \)
\( V=\frac{1}{3}\pi\cdot16\cdot9 \)
\( V=\frac{144\pi}{3} \)
\( V=\mathbf{48\pi\ \text{cm}^3} \) (≈ \(150.8\ \text{cm}^3\))

Exemplo 2 — Área Total conhecendo a geratriz

Enunciado. Um cone tem \( R=3 \) cm e \( g=5 \) cm. Determine \( A_T \).

Ver solução

\( A_L=\pi R g=\pi\cdot3\cdot5=15\pi \)
\( A_b=\pi R^2=\pi\cdot9=9\pi \)
\( A_T=A_b+A_L=9\pi+15\pi=\mathbf{24\pi\ \text{cm}^2} \) (≈ \(75.4\ \text{cm}^2\))

Exemplo 3 — Encontrando a geratriz

Enunciado. Num cone reto, \( R=6 \) cm e \( H=8 \) cm. Calcule \( g \).

Ver solução

\( g^2=R^2+H^2 \)
\( g^2=6^2+8^2=36+64=100 \)
\( g=\mathbf{10\ \text{cm}} \)

📘 eBook Grátis — Fórmulas Matemática

Volume e áreas de cones, cilindros, prismas, pirâmides e muito mais — tudo organizado para revisão.

➡️ Baixar Agora

Exercícios Propostos

Resolva e confira o gabarito em cada questão. Para mais listas, acesse o Banco de Questões e a coleção 10 eBooks. Revise rapidamente nos Mapas Mentais.

1) Calcule o volume de um cone com \( R=5 \) cm e \( H=12 \) cm.

Ver solução

\( V=\frac{1}{3}\pi R^2 H \)
\( V=\frac{1}{3}\pi\cdot25\cdot12 \)
\( V=\frac{300\pi}{3} \)
\( V=\mathbf{100\pi\ \text{cm}^3} \)

2) (Múltipla escolha) Num cone reto com \( R=4 \) cm e \( H=3 \) cm, a geratriz vale:

4 cm
5 cm
6 cm
7 cm

Ver solução

\( g=\sqrt{R^2+H^2}=\sqrt{4^2+3^2}=\sqrt{25}= \mathbf{5\ \text{cm}} \). Alternativa B.

3) Um cone tem \( R=3 \) cm e \( g=6 \) cm. Determine \( A_L \).

Ver solução

\( A_L=\pi R g=\pi\cdot3\cdot6=\mathbf{18\pi\ \text{cm}^2} \)

4) O volume é \( 48\pi\ \text{cm}^3 \) para um cone de raio \( R=4 \) cm. Encontre \( H \).

Ver solução

\( \frac{1}{3}\pi R^2 H = 48\pi \Rightarrow \frac{1}{3}\cdot16\cdot H = 48 \Rightarrow \frac{16H}{3}=48 \Rightarrow H=9\ \text{cm} \)

5) (Múltipla escolha) Dobrar simultaneamente \(R\) e \(H\) faz o volume:

duplicar
triplicar
quadruplicar
octuplicar

Ver solução

\( V \propto R^2 H \). Se \( R\to2R \) e \( H\to2H \): \( V\to 4\cdot2= \mathbf{8V} \). Alternativa D.

6) Um cone tem \( A_T=100\pi \) cm² e \( R=5 \) cm. Encontre \( g \).

Ver solução

\( A_T=\pi R^2 + \pi R g=100\pi \Rightarrow 25\pi + 5\pi g = 100\pi \Rightarrow 5g = 75 \Rightarrow g=\mathbf{15\ \text{cm}} \)

7) Para \( R=7 \) cm e \( g=25 \) cm, calcule \( H \).

Ver solução

\( g^2=R^2+H^2 \Rightarrow H=\sqrt{25^2-7^2}=\sqrt{625-49}=\sqrt{576}= \mathbf{24\ \text{cm}} \)

8) Um cone metálico (\( R=10\ \text{cm},\ H=30\ \text{cm} \)) será pintado apenas por fora (lateral + base). Qual a área a ser pintada?

Ver solução

\( g=\sqrt{10^2+30^2}=\sqrt{100+900}=\sqrt{1000}=10\sqrt{10} \)
\( A_L=\pi R g=\pi\cdot10\cdot10\sqrt{10}=100\pi\sqrt{10} \)
\( A_b=\pi R^2=100\pi \)
Área total externa: \( A_T=100\pi + 100\pi\sqrt{10} \) cm²

9) Sabendo que o setor da planificação tem raio \( g \) e ângulo \( \theta \), encontre \( \theta \) em função de \( R \) e \( g \).

Ver solução

Comprimento do arco = \( g\theta = 2\pi R \Rightarrow \theta = \dfrac{2\pi R}{g} \) (em radianos).

10) (Teoria) Assinale a alternativa falsa: