Cone: fórmulas completas, intuição, exemplos e exercícios
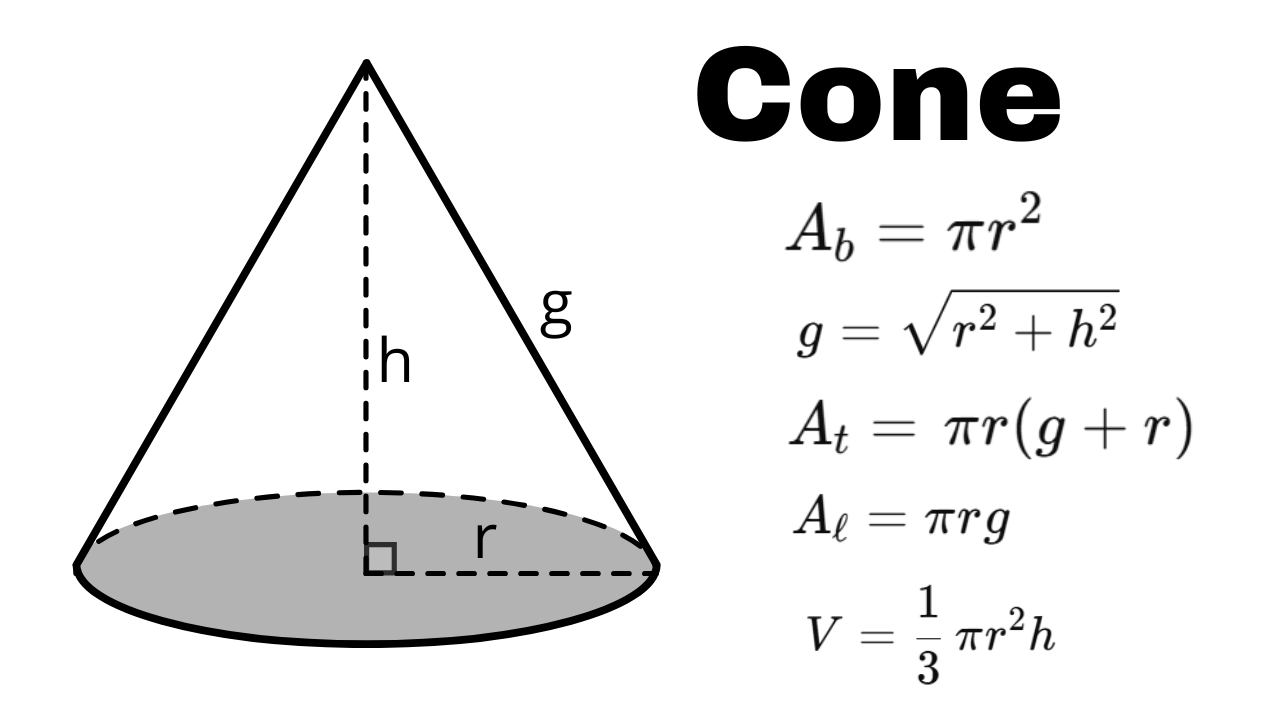
O cone é um dos principais corpos redondos. Neste guia reunimos as fórmulas do cone circular reto (o mais cobrado), a planificação, o tronco do cone e uma lista de exercícios. Para comparar com outros sólidos, veja esfera, cubo e paralelepípedo. Para treinar mais, acesse exercício esfera.
Notação
- \(r\): raio da base (círculo); \(d=2r\): diâmetro;
- \(h\): altura do cone (distância do vértice ao centro da base);
- \(g\): geratriz (aresta inclinada) — no cone reto: \( \displaystyle g=\sqrt{r^{2}+h^{2}} \).
Fórmulas do cone circular reto
Planificação (setor circular)
Ao “abrir” a lateral do cone, obtemos um setor de círculo de raio \(g\). O comprimento do arco do setor é igual à circunferência da base: \(L=2\pi r\). Se \(\alpha\) é o ângulo do setor em graus, então \(\displaystyle \frac{\alpha}{360}=\frac{L}{2\pi g}=\frac{r}{g}\Rightarrow \alpha=360\cdot\frac{r}{g}\). Em radianos: \(\theta = \dfrac{L}{g}=\dfrac{2\pi r}{g}\).
Tronco do cone (bônus)
Para um tronco (corte paralelo à base) com raios \(r_1>r_2\), altura \(h\) e geratriz \( \displaystyle g=\sqrt{(r_1-r_2)^{2}+h^{2}}\):
- Área lateral: \( \displaystyle A_\ell=\pi (r_1+r_2)\,g \)
- Área total: \( \displaystyle A_t=A_\ell+\pi r_1^{2}+\pi r_2^{2} \)
- Volume: \( \displaystyle V=\frac{1}{3}\pi h\,(r_1^{2}+r_1r_2+r_2^{2}) \)
Erros comuns
- Trocar \(g\) por \(h\) em \(A_\ell=\pi r g\).
- Esquecer que volume usa \(h\) (altura) e não \(g\).
- Unidades: áreas em cm²/m², volume em cm³/m³.
Exemplos resolvidos (cada passo em linha)
Exemplo 1 — Todas as grandezas a partir de \(r\) e \(h\). Para \(r=3\ \text{cm}\) e \(h=4\ \text{cm}\):
Exemplo 2 — Ângulo da planificação. Um cone tem \(r=4\ \text{cm}\) e \(g=10\ \text{cm}\). O ângulo do setor (graus) é:
Exemplo 3 — Tronco do cone. Para \(r_1=6\ \text{cm}\), \(r_2=4\ \text{cm}\) e \(h=8\ \text{cm}\):
Exercícios (múltipla escolha, com soluções)
1) Em um cone de raio \(r=4\ \text{cm}\) e altura \(h=9\ \text{cm}\), o volume é:
- \(36\pi\ \text{cm}^{3}\)
- \(40\pi\ \text{cm}^{3}\)
- \(44\pi\ \text{cm}^{3}\)
- \(48\pi\ \text{cm}^{3}\)
Ver solução
Resposta: D.
2) Para um cone com \(r=5\ \text{cm}\) e \(h=12\ \text{cm}\), calcule \(g\) e \(A_\ell\).
- \(g=12,\ A_\ell=60\pi\)
- \(g=13,\ A_\ell=65\pi\)
- \(g=13,\ A_\ell=60\pi\)
- \(g=12,\ A_\ell=65\pi\)
Ver solução
Resposta: B.
3) Sabe-se que \(A_t=96\pi\ \text{cm}^{2}\) para um cone com \(r=6\ \text{cm}\). Encontre \(g\) e \(h\).
- \(g=8,\ h=\sqrt{28}\)
- \(g=10,\ h=8\)
- \(g=12,\ h=6\)
- \(g=10,\ h=6\)
Ver solução
Resposta: B.
4) Um cone tem diâmetro \(d=10\ \text{cm}\) (logo \(r=5\ \text{cm}\)) e altura \(h=12\ \text{cm}\). A área total é:
- \(80\pi\ \text{cm}^{2}\)
- \(85\pi\ \text{cm}^{2}\)
- \(90\pi\ \text{cm}^{2}\)
- \(95\pi\ \text{cm}^{2}\)
Ver solução
Resposta: C.
5) (Cone oblíquo) A base tem raio \(r=2\ \text{cm}\) e a distância do vértice ao plano da base (altura) é \(h=6\ \text{cm}\). O volume é:
- \(8\pi\ \text{cm}^{3}\)
- \(12\pi\ \text{cm}^{3}\)
- \(16\pi\ \text{cm}^{3}\)
- \(24\pi\ \text{cm}^{3}\)
Ver solução
Resposta: A.
6) (Planificação) Para \(r=4\ \text{cm}\) e \(g=10\ \text{cm}\), o ângulo do setor (graus) é:
- \(120^\circ\)
- \(135^\circ\)
- \(144^\circ\)
- \(160^\circ\)
Ver solução
Resposta: C.
7) (Tronco) Para \(r_1=6\ \text{cm}\), \(r_2=4\ \text{cm}\) e \(h=8\ \text{cm}\), a área lateral do tronco é:
- \(10\pi\sqrt{17}\ \text{cm}^{2}\)
- \(20\pi\sqrt{17}\ \text{cm}^{2}\)
- \(30\pi\sqrt{17}\ \text{cm}^{2}\)
- \(40\pi\sqrt{17}\ \text{cm}^{2}\)
Ver solução
Resposta: B.
8) (Tronco) Para \(r_1=5\ \text{cm}\), \(r_2=3\ \text{cm}\) e \(h=7\ \text{cm}\), o volume é:
- \(\dfrac{245}{3}\pi\ \text{cm}^{3}\)
- \(\dfrac{301}{3}\pi\ \text{cm}^{3}\)
- \(\dfrac{343}{3}\pi\ \text{cm}^{3}\)
- \(\dfrac{361}{3}\pi\ \text{cm}^{3}\)
Ver solução
Resposta: C.
9) Um cone tem volume \(V=96\pi\ \text{cm}^{3}\) e raio \(r=4\ \text{cm}\). A altura é:
- \(12\ \text{cm}\)
- \(16\ \text{cm}\)
- \(18\ \text{cm}\)
- \(24\ \text{cm}\)
Ver solução
Resposta: C.
10) Um cone possui área lateral \(A_\ell=36\pi\ \text{cm}^{2}\) e raio \(r=3\ \text{cm}\). Encontre \(g\) e \(h\).
- \(g=9,\ h=6\sqrt{2}\)
- \(g=12,\ h=3\sqrt{15}\)
- \(g=12,\ h=9\)
- \(g=9,\ h=12\)
Ver solução
Resposta: B.
11) (Aplicada) Um cone com \(r=2{,}5\ \text{m}\) e \(h=6\ \text{m}\) será pintado por fora (base + lateral). O preço é R$ 40,00 por m². O custo é:
- R$ 2.523,00
- R$ 2.827,40
- R$ 3.100,80
- R$ 3.456,00
Ver solução
Resposta: B.
12) Se em um cone multiplicamos \(r\) e \(h\) por \(3\), o volume novo fica:
- 3 vezes maior
- 6 vezes maior
- 9 vezes maior
- 27 vezes maior
Ver solução
Resposta: D.
Links internos para continuar
- Corpos redondos — visão geral (cilindro, cone, esfera…).
- Esfera — área e volume com aplicações.
- Poliedros para contraste: Cubo e Paralelepípedo.
- Mais prática: Exercício Esfera.






















