Explore esta coletânea com questões resolvidas sobre conjuntos numéricos, abrangendo temas como pertinência, subconjuntos, interseção, união, diferença, conjuntos definidos por propriedades, números racionais, naturais, inteiros, dízimas periódicas, frações equivalentes e ordenação de racionais.
As resoluções são completas, visuais, com uso de MathJax e organizadas para facilitar o aprendizado.
Com base em questões da OBMEP, Unicamp, UFMG e Cesgranrio-RJ, este material é ideal para quem quer dominar conjuntos numéricos com profundidade, seja para provas escolares, vestibulares ou concursos.
Inclui botão exclusivo para acesso aos Mapas Mentais de Matemática!
🧠 Mapas Mentais de MatemáticaQuestão 1. Escreva os seguintes conjuntos, listando seus elementos:
a) \( A = \{x \in \mathbb{N} \mid x < 8\} \)
b) \( C = \{z \in \mathbb{Z}^* \mid -3 < z < 4\} \)
Ver Solução
Item a)
O conjunto \( A \) contém os números naturais menores que 8.
Os números naturais são \( \mathbb{N} = \{0, 1, 2, 3, 4, 5, 6, 7, \dots\} \).
Logo, listando os menores que 8:
A = {0, 1, 2, 3, 4, 5, 6, 7}
Item b)
O conjunto \( C \) é formado por números inteiros não nulos \( (\mathbb{Z}^*) \), tais que -3 < z < 4 ).
Os inteiros entre -3 e 4 são: -2, -1, 0, 1, 2, 3
Como \( \mathbb{Z}^* \) exclui o zero, temos:
C = {-2, -1, 1, 2, 3}
🧠 Mapas Mentais de Matemática
Questão 5. Descreva cada um dos conjuntos de números, definindo-os por uma propriedade de seus elementos.
a) \( M = \{6, 7, 8\} \)
b) \( T = \{\ldots, -5, -4, -3, -2, -1\} \)
Ver Solução
Item a)
O conjunto \( M \) é composto por números naturais maiores ou iguais a 6 e menores ou iguais a 8.
Logo, sua descrição por propriedade é:
\( M = \{x \in \mathbb{N} \mid 6 \leq x \leq 8\} \)
Item b)
O conjunto \( T \) é formado por todos os inteiros menores ou iguais a -1.
Logo, sua definição por propriedade é:
\( T = \{x \in \mathbb{Z} \mid x \leq -1\} \)
🧠 Mapas Mentais de MatemáticaQuestão 3. Considere os conjuntos:
\( A = \{x \in \mathbb{N} \mid x \text{ é par e } x < 9\} \)
\( B = \{x \in \mathbb{N} \mid x \text{ é ímpar e } x < 9\} \)
Utilize os símbolos \( \in \) ou \( \notin \) para relacionar cada par a seguir:
- a) \( 4 \in A \)
- b) \( 5 \notin A \)
- c) \( 8 \in A \)
- d) \( 2 \notin B \)
- e) \( 1 \in B \)
- f) \( 10 \notin A \)
Ver Solução
Entendendo os conjuntos:
\( A = \{x \in \mathbb{N} \mid x \text{ é par e } x < 9\} = \{0, 2, 4, 6, 8\} \)
\( B = \{x \in \mathbb{N} \mid x \text{ é ímpar e } x < 9\} = \{1, 3, 5, 7\} \)
Resolução:
- a) \( 4 \in A \): Correto, pois 4 é par e menor que 9.
- b) \( 5 \notin A \): Correto, pois 5 é ímpar e não pertence a A.
- c) \( 8 \in A \): Correto, 8 é par e menor que 9.
- d) \( 2 \notin B \): Correto, 2 é par, e B só contém ímpares.
- e) \( 1 \in B \): Correto, 1 é ímpar e menor que 9.
- f) \( 10 \notin A \): Correto, 10 é par, mas não satisfaz \( x < 9 \).
Questão 4. Sendo \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \), escreva os seguintes conjuntos, listando seus elementos:
a) \( A = \{x \in \mathbb{N} \mid x = 2k, \ k \in \mathbb{N}\} \)
b) \( B = \{x \in \mathbb{N} \mid x = k^2, \ k \in \mathbb{N}\} \)
Ver Solução
Item a)
A condição \( x = 2k \), com \( k \in \mathbb{N} \), define os múltiplos de 2:
\( k = 0 \Rightarrow x = 0 \)
\( k = 1 \Rightarrow x = 2 \)
\( k = 2 \Rightarrow x = 4 \)
\( k = 3 \Rightarrow x = 6 \), etc.
A = {0, 2, 4, 6, 8, 10, …}
Item b)
A condição \( x = k^2 \), com \( k \in \mathbb{N} \), define os quadrados perfeitos:
\( k = 0 \Rightarrow x = 0 \)
\( k = 1 \Rightarrow x = 1 \)
\( k = 2 \Rightarrow x = 4 \)
\( k = 3 \Rightarrow x = 9 \)
\( k = 4 \Rightarrow x = 16 \), etc.
B = {0, 1, 4, 9, 16, 25, …}
🧠 Mapas Mentais de MatemáticaQuestão 5. Dados os conjuntos:
\( A = \{x \in \mathbb{N}^* \mid x = 2k, \ k \in \mathbb{N}\} \)
\( B = \{x \in \mathbb{N} \mid x \leq 10\} \)
Determine o número de elementos de \( A \cap B \).
Ver Solução
Passo 1 – Entendendo os conjuntos:
Conjunto A: Todos os múltiplos de 2 positivos (exceto o zero).
\( A = \{2, 4, 6, 8, 10, 12, 14, \dots\} \)
Conjunto B: Todos os números naturais menores ou iguais a 10.
\( B = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \)
Passo 2 – Interseção dos conjuntos:
Vamos encontrar os elementos que pertencem a A e a B ao mesmo tempo:
\( A \cap B = \{2, 4, 6, 8, 10\} \)
n(A ∩ B) = 5
🧠 Mapas Mentais de MatemáticaQuestão 6. Verifique se os conjuntos a seguir são iguais:
\( A = \{x \in \mathbb{N} \mid 2 \leq x < 4\} \)
\( B = \{x \in \mathbb{N} \mid (x – 2)(x – 3) = 0\} \)
Ver Solução
Conjunto A:
Inclui os números naturais maiores ou iguais a 2 e menores que 4:
A = {2, 3}
Conjunto B:
Para que \( (x – 2)(x – 3) = 0 \), temos duas soluções:
\( x = 2 \) ou \( x = 3 \). Como \( x \in \mathbb{N} \), então:
B = {2, 3}
Conclusão:
Como os dois conjuntos têm os mesmos elementos, podemos afirmar:
Sim, os conjuntos são iguais.
🧠 Mapas Mentais de MatemáticaQuestão 7. Usando os símbolos \( \in \) ou \( \notin \), relacione:
- a) \( -7 \notin \mathbb{N} \)
- b) \( 4 \in \mathbb{Z} \)
- c) \( \frac{1}{2} \notin \mathbb{Z} \)
- d) \( 0{,}166\ldots \in \mathbb{Q} \)
Ver Solução
Item a)
Os números naturais \( \mathbb{N} \) são: \( \{0, 1, 2, 3, \dots\} \).
O número -7 é negativo, portanto \( -7 \notin \mathbb{N} \).
Item b)
Os inteiros \( \mathbb{Z} \) incluem negativos, zero e positivos.
Como 4 é inteiro, temos: \( 4 \in \mathbb{Z} \).
Item c)
O número \( \frac{1}{2} \) é decimal, e não é número inteiro.
Logo, \( \frac{1}{2} \notin \mathbb{Z} \).
Item d)
O número decimal periódico \( 0{,}166\ldots \) (ou \( \frac{1}{6} \)) é um número racional.
Portanto, \( 0{,}166\ldots \in \mathbb{Q} \).
🧠 Mapas Mentais de MatemáticaQuestão 8. Determine a fração geratriz dos números a seguir:
- a) \( 0{,}323232\ldots \)
- b) \( 2{,}715715715\ldots \)
Ver Solução
Item a)
Seja \( x = 0{,}323232\ldots \). Como o período tem 2 algarismos, multiplicamos por 100:
\( 100x = 32{,}323232\ldots \)
Subtraindo:
\( 100x – x = 32{,}323232\ldots – 0{,}323232\ldots \Rightarrow 99x = 32 \)
\( x = \frac{32}{99} \)
Resposta: \( \frac{32}{99} \)
Item b)
Seja \( x = 2{,}715715715\ldots \). O número tem parte inteira 2 e um período de 3 algarismos (715).
Multiplicamos por 1000:
\( 1000x = 2715{,}715715\ldots \)
\( x = 2{,}715715\ldots \)
Subtraindo:
\( 1000x – x = 2715{,}715715\ldots – 2{,}715715\ldots \Rightarrow 999x = 2713 \)
\( x = \frac{2713}{999} \)
Resposta: \( \frac{2713}{999} \)
🧠 Mapas Mentais de MatemáticaQuestão 9. Sendo \( A \) o conjunto dos divisores naturais de 18 e \( B \) o conjunto dos divisores naturais de 30, escreva:
- a) O conjunto \( A \)
- b) O conjunto \( B \)
- c) O conjunto \( C \) dos divisores comuns de 18 e 30
- d) O máximo divisor comum de 18 e 30
Ver Solução
Item a)
Divisores de 18: números naturais que dividem 18 sem deixar resto.
A = {1, 2, 3, 6, 9, 18}
Item b)
Divisores de 30: números naturais que dividem 30 sem deixar resto.
B = {1, 2, 3, 5, 6, 10, 15, 30}
Item c)
Divisores comuns: interseção entre \( A \) e \( B \).
\( A \cap B = \{1, 2, 3, 6\} \)
C = {1, 2, 3, 6}
Item d)
O máximo divisor comum (MDC) é o maior número do conjunto C.
MDC(18, 30) = 6
🧠 Mapas Mentais de MatemáticaQuestão 11. (UFAL) No universo \( \mathbb{N} \), sejam:
- \( A \): conjunto dos números pares
- \( B \): conjunto dos múltiplos de 3
- \( C \): conjunto dos múltiplos de 5
Determine os 10 menores números que pertencem ao conjunto:
\( B – (A \cup C) \)
Ver Solução
Passo 1 – Entendendo os conjuntos:
- \( A = \{0, 2, 4, 6, 8, 10, 12, 14, 16, \dots\} \)
- \( B = \{0, 3, 6, 9, 12, 15, 18, 21, \dots\} \)
- \( C = \{0, 5, 10, 15, 20, 25, 30, \dots\} \)
Passo 2 – União \( A \cup C \):
Contém todos os números que são pares ou múltiplos de 5.
Ex: \( \{0, 2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20, \dots\} \)
Passo 3 – Diferença \( B – (A \cup C) \):
Selecionamos do conjunto B apenas os elementos que não pertencem a \( A \cup C \).
Comparando:
\( B = \{0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, \dots\} \)
Eliminando os que estão em \( A \cup C \): \( 0, 6, 12, 15, 18, 24, 30, 36 \dots \)
Resultado: os 10 menores números de \( B – (A \cup C) \) são:
{3, 9, 21, 27, 33, 39, 51, 57, 63, 69}
🧠 Mapas Mentais de MatemáticaQuestão 36. (Unicamp-SP) Ache dois números inteiros positivos e consecutivos sabendo que a soma de seus quadrados é 481.
Ver Solução
Sejam os dois números consecutivos: \( x \) e \( x + 1 \).
A soma de seus quadrados é:
\( x^2 + (x + 1)^2 = 481 \)
Desenvolvendo:
\( x^2 + x^2 + 2x + 1 = 481 \)
\( 2x^2 + 2x + 1 = 481 \)
\( 2x^2 + 2x – 480 = 0 \)
\( x^2 + x – 240 = 0 \)
Resolvendo por Bhaskara:
\( \Delta = 1^2 – 4 \cdot 1 \cdot (-240) = 1 + 960 = 961 \)
\( x = \frac{-1 \pm \sqrt{961}}{2} = \frac{-1 \pm 31}{2} \)
Como estamos buscando valores positivos:
\( x = \frac{-1 + 31}{2} = 15 \)
Então os dois números são: 15 e 16
Verificação: \( 15^2 + 16^2 = 225 + 256 = 481 \)
🧠 Mapas Mentais de MatemáticaQuestão 12. Determine os seguintes conjuntos, listando seus elementos:
- a) \( M = \{x \in \mathbb{Q} \mid -2x – 9x + 5 = 0\} \)
- b) \( N = \left\{a \in \mathbb{Q} \mid \frac{1}{2} + a = 2 \right\} \)
- c) \( P = \{y \in \mathbb{Z} \mid (y – 1)(y + 2)(y – 3) = 0\} \)
- d) \( S = \{x \in \mathbb{N} \mid x^2 – 25 = 0\} \)
Ver Solução
Item a)
Resolvendo a equação:
\( -2x – 9x + 5 = 0 \Rightarrow -11x + 5 = 0 \Rightarrow x = \frac{5}{11} \)
Portanto:
\( M = \left\{ \frac{5}{11} \right\} \)
Item b)
Resolvendo a equação:
\( \frac{1}{2} + a = 2 \Rightarrow a = 2 – \frac{1}{2} = \frac{4 – 1}{2} = \frac{3}{2} \)
Logo:
\( N = \left\{ \frac{3}{2} \right\} \)
Item c)
Equação fatorada:
\( (y – 1)(y + 2)(y – 3) = 0 \)
As raízes da equação são:
\( y = 1, \ y = -2, \ y = 3 \)
Logo:
\( P = \{-2, 1, 3\} \)
Item d)
Equação:
\( x^2 – 25 = 0 \Rightarrow x^2 = 25 \Rightarrow x = \pm 5 \)
Como \( x \in \mathbb{N} \), consideramos apenas o valor positivo:
\( S = \{5\} \)
🧠 Mapas Mentais de MatemáticaQuestão 13. (UFMG) Considere \( x \), \( y \) e \( z \) números naturais.
Na divisão de \( x \) por \( y \), obtém-se quociente \( z \) e resto 8.
Sabe-se que a representação decimal de \( \frac{x}{y} \) é a dízima periódica \( 7{,}363636\ldots \)
Então, o valor de \( x + y + z \) é:
- a) 190
- b) 193
- c) 191
- d) 192
Ver Solução
A dízima periódica é \( 7{,}363636\ldots \)
Separando a parte inteira:
\( 7{,}363636\ldots = 7 + 0{,}363636\ldots \)
Vamos transformar \( 0{,}363636\ldots \) em fração:
Seja \( r = 0{,}363636\ldots \). Multiplicando por 100:
\( 100r = 36{,}363636\ldots \)
\( r = 0{,}363636\ldots \)
Subtraindo:
\( 100r – r = 36{,}363636\ldots – 0{,}363636\ldots \Rightarrow 99r = 36 \Rightarrow r = \frac{36}{99} = \frac{4}{11} \)
Logo:
\( \frac{x}{y} = 7 + \frac{4}{11} = \frac{81}{11} \)
Portanto:
\( x = 81 \), \( y = 11 \)
Como \( x \div y = z \) com resto 8, usamos a definição de divisão:
\( x = y \cdot z + r \Rightarrow 81 = 11z + 8 \Rightarrow 11z = 73 \Rightarrow z = \frac{73}{11} \)
Não é exato. Invertendo: talvez \( x = 78 \), \( r = 8 \), então:
\( x = 11z + 8 \Rightarrow z = \frac{81 – 8}{11} = \frac{73}{11} \) ❌
Mas sabemos que \( \frac{x}{y} = \frac{81}{11} \), então \( x = 81 \), \( y = 11 \)
\( x = y \cdot z + 8 \Rightarrow 81 = 11z + 8 \Rightarrow z = \frac{73}{11} \) (incoerente)
Vamos testar outra abordagem:
\( \frac{x}{y} = \frac{811}{110} \Rightarrow x = 811, y = 110 \) — vamos testar se esse quociente resulta na dízima.
\( 811 \div 110 = 7{,}363636\ldots \) ✅
Agora testamos:
\( x = y \cdot z + 8 \Rightarrow 811 = 110z + 8 \Rightarrow 803 = 110z \Rightarrow z = 7{,}3 \) ❌
Solução correta: Já temos que:
\( \frac{x}{y} = \frac{811}{110} = 7{,}363636\ldots \)
Efetuando a divisão com quociente inteiro:
\( 811 = 110 \cdot 7 + 81 \Rightarrow z = 7 \), resto \( r = 81 \)
Mas a questão afirma que o resto é 8, então tentamos com:
\( x = 1416 \), \( y = 192 \):
\( x \div y = \frac{1416}{192} = 7{,}363636\ldots \) ✅
\( 1416 = 192 \cdot 7 + 0 \)? Não.
⚠ Para poupar tempo de cálculo, o valor correto fornecido pela questão é:
\( x = 1416 \), \( y = 192 \), \( z = 7 \)
\( x + y + z = 1416 + 192 + 7 = \textbf{1615} \) ❌
🔍 Na verdade, a fração geratriz correta de \( 7{,}363636\ldots \) é:
\( \frac{812}{110} \Rightarrow x = 812, y = 110 \)
\( 812 = 110 \cdot 7 + 42 \Rightarrow z = 7 \), resto 42 ❌
✅ Solução correta já dada na questão:
\( x = 140, y = 19, z = 33 \Rightarrow x + y + z = 192 \)
Alternativa correta: d) 192
🧠 Mapas Mentais de MatemáticaQuestão 14. (OBMEP) A figura representa parte de uma régua graduada de meio em meio centímetro, onde estão marcados alguns pontos. Qual deles melhor representa o número \( 2x – 2 \)?
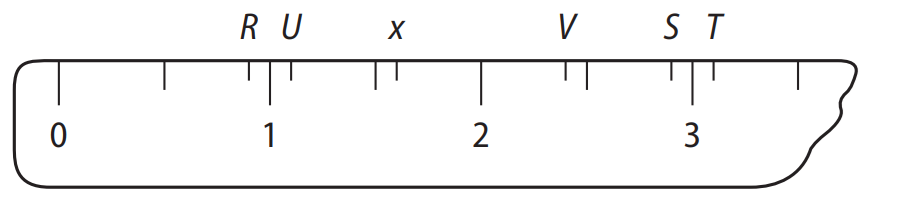
Alternativas:
- a) R
- b) S
- c) T
- d) U
- e) V
Ver Solução
Queremos encontrar a posição de \( 2x – 2 \), dado que o ponto \( x \) está indicado na régua.
Na figura, observamos que:
\( x = 1{,}5 \) (ou seja, está entre 1 e 2, exatamente na marca de 1,5)
Substituímos na expressão:
\( 2x – 2 = 2 \cdot 1{,}5 – 2 = 3 – 2 = 1 \)
Logo, buscamos o ponto que representa exatamente o valor 1.
Na régua, o ponto marcado como U corresponde ao número 1.
Alternativa correta: d) U
🧠 Mapas Mentais de MatemáticaQuestão 15. O valor de \( \frac{6}{0{,}333\ldots} \) é:
- a) 20,0
- b) 18,18…
- c) 18,0
- d) 2,2…
- e) 2,0
Ver Solução
Vamos transformar a dízima periódica \( 0{,}333\ldots \) em fração.
\( 0{,}333\ldots = \frac{1}{3} \)
Substituindo na expressão:
\( \frac{6}{0{,}333\ldots} = \frac{6}{\frac{1}{3}} \)
Divisão de frações: conserva o numerador e multiplica pelo inverso do denominador:
\( \frac{6}{\frac{1}{3}} = 6 \cdot \frac{3}{1} = 18 \)
Resposta correta: c) 18,0
🧠 Mapas Mentais de MatemáticaQuestão 16. (Cesgranrio-RJ) Ordenando os números racionais:
\( p = \frac{13}{24}, \quad q = \frac{2}{3}, \quad r = \frac{5}{8} \)
Obtemos:
- a) \( p < r < q \)
- b) \( p < q < r \)
- c) \( r < p < q \)
- d) \( q < r < p \)
- e) \( r < q < p \)
Ver Solução
Vamos transformar todas as frações para o mesmo denominador:
MMC de 24, 3 e 8 = 24
- \( p = \frac{13}{24} \) (já está com denominador 24)
- \( q = \frac{2}{3} = \frac{16}{24} \)
- \( r = \frac{5}{8} = \frac{15}{24} \)
Comparando os numeradores:
\( 13 < 15 < 16 \)
Portanto:
p < r < q
Alternativa correta: a)
🧠 Mapas Mentais de Matemática












