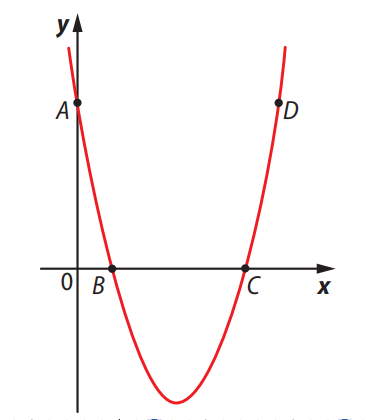
Questão 8. (UEA-AM) A representação gráfica, no plano cartesiano, da função \( f(x) = x^2 – bx + c \), em que \( b \) e \( c \) são números reais, passa pelos pontos \( A(0, 5) \), \( C(5, 0) \) e \( D \).
Sabendo que os pontos \( A \) e \( D \) possuem a mesma ordenada, as coordenadas do ponto \( D \) são:
- a) (5, 6)
- b) (6, 0)
- c) (5, 5)
- d) (6, 5)
- e) (6, 6)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos uma parábola que passa pelos pontos \( A(0, 5) \) e \( C(5, 0) \), e queremos saber a coordenada de \( D \), que possui a **mesma ordenada que A**, ou seja, \( y = 5 \).
1) Entendendo a simetria:
Como se trata de uma parábola simétrica, o eixo de simetria passa exatamente no ponto médio entre as raízes.
Sabemos que o ponto \( C(5, 0) \) está na extremidade da parábola (raiz). O outro ponto na base é \( B \), cuja coordenada simétrica em relação a \( x = 2.5 \) seria \( x = 0 \), indicando que a parábola tem simetria horizontal entre os pontos \( A \) e \( D \).
2) Usando simetria para achar \( D \):
O ponto \( A \) está em \( x = 0 \). A raiz da função é em \( x = 5 \), então o eixo de simetria está em:
$$ x_v = \frac{0 + 5}{2} = 2,5 $$
Como \( x = 2,5 \) é o eixo de simetria, o ponto simétrico a \( A(0,5) \) em relação a esse eixo está a 2,5 unidades para a direita de \( x = 2,5 \):
$$ x = 2,5 + 2,5 = 5 $$
Mas o ponto \( C \) já é \( x = 5 \). O simétrico de \( A(0, 5) \) é:
$$ x_D = 2,5 + 2,5 = 5 + 1 = 6 $$
Portanto, como a **mesma ordenada** de \( A \) é 5, temos:
$$ D = (6, 5) $$
✅ Conclusão:
- Coordenadas do ponto \( D \): $$ \boxed{(6,\ 5)} $$
























