Quando uma função é crescente?

Em um intervalo I, f é crescente quando para quaisquer x1<x2 em I temos f(x1) <= f(x2). Se a desigualdade é estrita, diz-se estritamente crescente.

Quando é decrescente?

Em I, f é decrescente quando x1 = f(x2). Se a desigualdade é estrita, diz-se estritamente decrescente.

Como decidir olhando um gráfico?

Leia o gráfico da esquerda para a direita. Se a curva sobe, é crescente; se desce, é decrescente; se permanece na mesma altura, é constante.

Qual a relação com f(x)=ax+b?

Para a≠0, o sinal de a define tudo: a>0 → crescente em ℝ; a<0 → decrescente em ℝ; a=0 → constante. O zero x0=−b/a não muda a monotonicidade.

Canal do WhatsApp
Acesso Imediato

Canal do Instagram
Acesso Imediato

Crescimento e decrescimento de funções

Q: Quando é decrescente?

Em I, f é decrescente quando x1 = f(x2). Se a desigualdade é estrita, diz-se estritamente decrescente.

Q: Como decidir olhando um gráfico?

Leia o gráfico da esquerda para a direita. Se a curva sobe, é crescente; se desce, é decrescente; se permanece na mesma altura, é constante.

Q: Qual a relação com f(x)=ax+b?

Para a≠0, o sinal de a define tudo: a>0 → crescente em ℝ; a<0 → decrescente em ℝ; a=0 → constante. O zero x0=−b/a não muda a monotonicidade.

Crescimento e Decrescimento de Funções: definição, gráfico, tabela, exemplos e exercícios

Crescimento e decrescimento de funções

Aprenda a reconhecer funções crescentes, decrescentes e constantes no gráfico, na tabela e pela própria lei. Este conteúdo conversa com a série de função afim: Afim: crescente x decrescente Gráfico do 1º grau Como construir o gráfico Taxa de variação Zero da função Estudo do sinal

Gráfico com trechos crescentes e decrescentes e pontos A, B, C, D, E marcando máximos e mínimos locais

Definições formais (em intervalos)

\[ \textbf{Crescente em } I:\quad \forall\, x_1\lt x_2\in I \Rightarrow f(x_1)\le f(x_2). \]

\[ \textbf{Decrescente em } I:\quad \forall\, x_1\lt x_2\in I \Rightarrow f(x_1)\ge f(x_2). \]

\[ \textbf{Constante em } I:\quad \forall\, x_1,x_2\in I,\ f(x_1)=f(x_2). \]

Quando as desigualdades são estritas ($\lt$ e $\gt$), usamos “estritamente crescente/decrescente”.

Como identificar no gráfico

Leia sempre da esquerda para a direita: subiu ⇒ crescente; desceu ⇒ decrescente; manteve ⇒ constante.
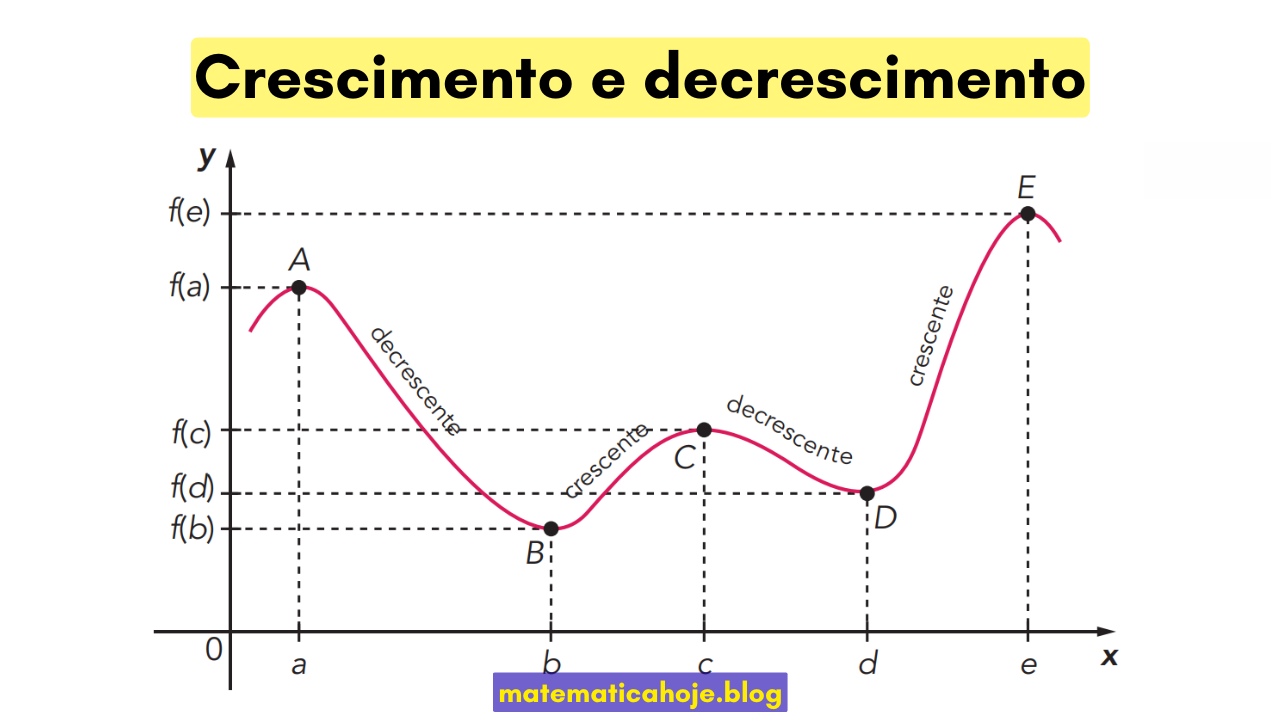
Mudanças de tendência ocorrem em pontos de máximo/mínimo locais (ex.: A, B, C, D, E na figura).
Para retas $f(x)=ax+b$: o sinal de $a$ decide tudo (veja o critério geral).

Como decidir a partir de uma tabela

Ordene os $x$ e observe a sequência de $f(x)$. Se aumenta, é crescente; se diminui, decrescente; se repete, constante.

Relação com a taxa de variação

\[ \frac{\Delta y}{\Delta x}=\frac{f(x_2)-f(x_1)}{x_2-x_1}. \]

Se $\Delta y/\Delta x\gt 0$ no intervalo → crescente; $\lt 0$ → decrescente; $=0$ → constante. Para a reta, $\Delta y/\Delta x=a$. Relembre em Δy/Δx.

📘 Precisa revisar fórmulas rapidamente?

Tenha o eBook Fórmulas Matemática com resumos de funções, gráficos, sinais, geometria e muito mais — ideal para ENEM e vestibulares.

Baixar eBook de Fórmulas

Exemplos resolvidos

Exemplo 1 — Leitura do gráfico (A→E). No gráfico da figura, considere $a\lt b\lt c\lt d\lt e$. a) Indique intervalos de crescimento/decrescimento. b) Classifique A, C e E (máximo/mínimo local ou nenhum).

Ver solução

a) $(a,b)$: decrescente; $(b,c)$: crescente; $(c,d)$: decrescente; $(d,e)$: crescente.

b) A: máx. local; B: mín. local; C: máx. local; D: mín. local; E: máx. local.

Exemplo 2 — Funções afins. Para $f(x)=3x-2$ e $g(x)=-1{,}5x+4$: classifique a monotonicidade e informe o zero de cada uma.

Ver solução

$f$: $a=3\gt 0$ ⇒ crescente em $\mathbb{R}$, zero $x_0=2/3$. $g$: $a=-1{,}5\lt 0$ ⇒ decrescente, zero $x_0\approx 2{,}67$. Zero da função.

Exemplo 3 — Tabela de valores. Dada a tabela, determine a monotonicidade em $[1,5]$.

$x$	1	2	3	4	5
$f(x)$	8	6	4	4	3

Ver solução

1→3: decrescente; 3→4: constante; 4→5: decrescente. No todo, não é monótona.

Erros comuns

Ler o gráfico da direita para a esquerda (padrão é esquerda → direita).
Confundir “maior imagem” com “maior crescimento”. Crescimento é sobre variação, não sobre altura.
Ignorar o intervalo: a mesma função pode crescer num trecho e decrescer em outro.

Exercícios propostos (com gabarito)

1) Classifique a monotonicidade de $h(x)=\dfrac{1}{2}x-7$ em $\mathbb{R}$. Ache o zero e explique por que ele não muda a classificação.

Gabarito

Crescente ($a=1/2\gt 0$). Zero $x_0=14$. O zero só indica onde cruza o eixo $x$; a inclinação continua positiva.

2) Seja $f(x)=\begin{cases} -2x+6,& 0\le x\le 2\\ x-1,& 2\lt x\le 5 \end{cases}$. Determine intervalos de crescimento/decrescimento.

Gabarito

$[0,2]$: decrescente ($a=-2$). $(2,5]$: crescente ($a=1$).

3) A tabela mostra a receita $R$ (R$) ao vender $q$ unidades a preço constante por unidade. Classifique e diga se pode ser função linear.

$q$	10	15	22	27
$R(q)$	80	120	176	216

Gabarito

Crescente. Como $R/q\approx 8$ constante, é proporcionalidade direta ⇒ função linear $R=8q$.

4) O gráfico de $p(x)$ é uma reta horizontal passando por $y=-3$. Classifique e diga se tem zero.

Gabarito

Constante (nem cresce nem decresce). Não tem zero. Função constante.

5) Em qual(is) intervalo(s) a função da figura inicial é estritamente crescente? E estritamente decrescente?

Gabarito

Crescente: $(b,c)$ e $(d,e)$. Decrescente: $(a,b)$ e $(c,d)$.

Continue estudando

Afim: crescente e decrescente Gráfico do 1º grau Como construir o gráfico Taxa de variação Zero da função Interseção de retas

Links de produtos do blog

Relacionadas

Definição de Função

Leitura e interpretação de gráficos

Gráfico: Domínio e Imagem

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.