CUNHA ESFÉRICA – Geometria Espacial

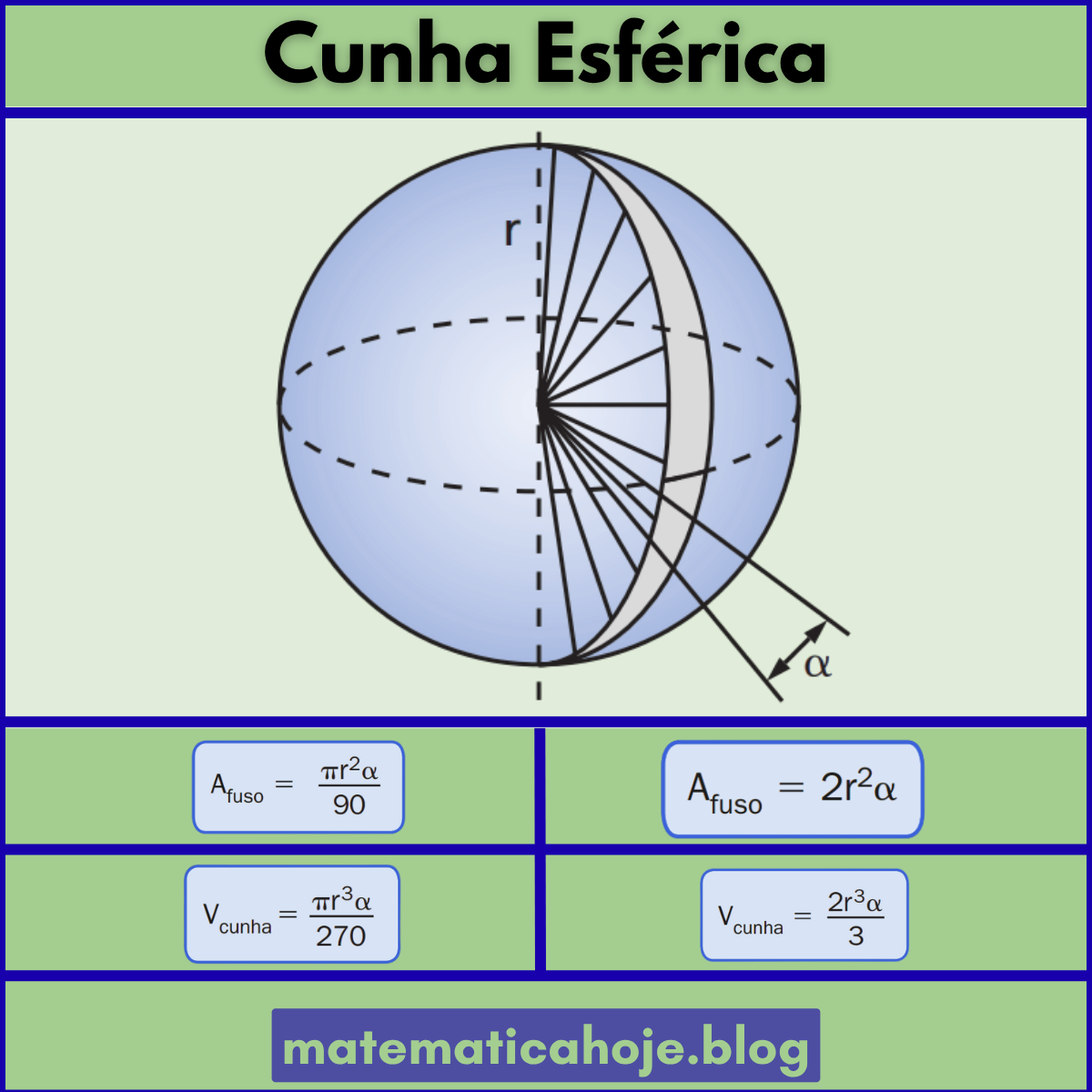
Cunha esférica em esfera de raio r, com ângulo diedro α; fórmulas em radianos e graus — Resumo visual da cunha esférica (setor esférico) – matematicaoje.blog

O que é uma cunha esférica?

A cunha esférica (também chamada de setor esférico) é a porção de uma esfera delimitada por dois semiplanos que passam pelo centro, formando um ângulo diedro \(\alpha\). A interseção com a superfície esférica gera um fuso esférico.

Mapas Mentais
🧠 Mapas Mentais de Matemática

Banco de Questões
📘 Pratique por assunto

ENEM Matemática
🎯 Guia do ENEM

10 eBooks
📚 Coleção completa

📘 Fórmulas (com \(\alpha\) em radianos)

Área do fuso esférico: \( A_{\text{fuso}} = 2\,r^{2}\,\alpha \)

Volume da cunha: \( V_{\text{cunha}} = \dfrac{2\alpha}{3}\,r^{3} \)

Observação: essas expressões vêm da proporção pelo ângulo sólido \(\Omega=2\alpha\): \(\dfrac{A_{\text{fuso}}}{4\pi r^2}=\dfrac{\Omega}{4\pi}\) e \(\dfrac{V_{\text{cunha}}}{\frac{4}{3}\pi r^3}=\dfrac{\Omega}{4\pi}\).

🧭 Se preferir \(\alpha\) em graus

Use \(\alpha_{\text{rad}}=\alpha_{\text{graus}}\cdot\dfrac{\pi}{180}\).

\(A_{\text{fuso}}=\dfrac{\pi r^{2}\,\alpha_{\text{graus}}}{90}\), \(V_{\text{cunha}}=\dfrac{\pi r^{3}\,\alpha_{\text{graus}}}{270}\).

Exemplo 1 (dados \(r\) e \(\alpha\) em graus)

Numa esfera de raio \( r=6\,\text{cm} \), considere \(\alpha=45^\circ\). Calcule \(A_{\text{fuso}}\) e \(V_{\text{cunha}}\).

\[ \begin{aligned} A_{\text{fuso}} &= \frac{\pi r^{2}\,\alpha}{90} \\ &= \frac{\pi \cdot 6^{2}\cdot 45}{90} \\ &= \frac{\pi \cdot 36 \cdot 45}{90} \\ &= 18\pi\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} V_{\text{cunha}} &= \frac{\pi r^{3}\,\alpha}{270} \\ &= \frac{\pi \cdot 6^{3}\cdot 45}{270} \\ &= \frac{\pi \cdot 216 \cdot 45}{270} \\ &= 36\pi\ \text{cm}^{3} \end{aligned}\]

📗 eBook de Fórmulas Matemáticas

Tenha todas as fórmulas de Geometria Espacial, Álgebra e Trigonometria prontas para consulta rápida.

📥 Baixar Agora

Exemplos Adicionais

Exemplo 2 (descobrindo \(\alpha\) pelo volume – rad). Uma cunha em esfera de raio \( r=5\,\text{cm} \) tem volume \( V= \, \mathbf{50}\pi\,\text{cm}^3 \). Encontre \(\alpha\) em radianos.

\[ \begin{aligned} V_{\text{cunha}} &= \frac{2\alpha}{3} r^{3} \\ 50\pi &= \frac{2\alpha}{3}\cdot 5^{3} \\ 50\pi &= \frac{2\alpha}{3}\cdot 125 \\ 50\pi &= \frac{250\alpha}{3} \\ \alpha &= \frac{150\pi}{250} \\ \alpha &= \frac{3\pi}{5}\ \text{rad} \end{aligned}\]

Exemplo 3 (descobrindo \(\alpha\) pela área do fuso – graus). Em uma esfera de raio \( r=7\,\text{cm} \), o fuso mede \( A_{\text{fuso}}= \mathbf{49}\pi\,\text{cm}^2 \). Determine \(\alpha\) em graus.

\[ \begin{aligned} A_{\text{fuso}} &= \frac{\pi r^{2}\,\alpha}{90} \\ 49\pi &= \frac{\pi \cdot 7^{2}\,\alpha}{90} \\ 49\pi &= \frac{\pi \cdot 49\,\alpha}{90} \\ 49 &= \frac{49\alpha}{90} \\ \alpha &= 90^\circ \end{aligned}\]

Exercícios de Múltipla Escolha

1. (Área do fuso – rad) Numa esfera de raio \( r=4\,\text{cm} \), a cunha tem \(\alpha=\dfrac{\pi}{6}\). A área do fuso é:

A) \( \dfrac{8\pi}{3}\ \text{cm}^2\)

B) \( \dfrac{16\pi}{3}\ \text{cm}^2\)

C) \( \dfrac{32\pi}{3}\ \text{cm}^2\)

D) \( 8\pi\ \text{cm}^2\)

👀 Ver solução passo a passo

\[ \begin{aligned} A_{\text{fuso}} &= 2 r^{2}\alpha \\ &= 2\cdot 4^{2}\cdot \frac{\pi}{6} \\ &= 2\cdot 16 \cdot \frac{\pi}{6} \\ &= \frac{32\pi}{6} \\ &= \frac{16\pi}{3}\ \text{cm}^{2} \end{aligned}\]

Gabarito: B.

2. (Volume – graus) Para uma esfera de raio \( r=9\,\text{cm} \) e \(\alpha=30^\circ\), o volume da cunha é:

A) \(27\pi\ \text{cm}^3\)

B) \(54\pi\ \text{cm}^3\)

C) \(81\pi\ \text{cm}^3\)

D) \(162\pi\ \text{cm}^3\)

👀 Ver solução passo a passo

\[ \begin{aligned} V_{\text{cunha}} &= \frac{\pi r^{3}\,\alpha}{270} \\ &= \frac{\pi \cdot 9^{3} \cdot 30}{270} \\ &= \frac{\pi \cdot 729 \cdot 30}{270} \\ &= \frac{729\pi}{9} \\ &= 81\pi\ \text{cm}^{3} \end{aligned}\]

Gabarito: C.

3. (Encontrando \(\alpha\) – rad) Uma cunha em esfera de raio \( r=3\,\text{cm} \) tem volume \( V= 6\pi\,\text{cm}^3 \). Qual é \(\alpha\) (em rad)?

A) \( \dfrac{\pi}{3} \)

B) \( \dfrac{\pi}{2} \)

C) \( \dfrac{2\pi}{3} \)

D) \( \pi \)

👀 Ver solução passo a passo

\[ \begin{aligned} V_{\text{cunha}} &= \frac{2\alpha}{3} r^{3} \\ 6\pi &= \frac{2\alpha}{3}\cdot 3^{3} \\ 6\pi &= \frac{2\alpha}{3}\cdot 27 \\ 6\pi &= 18\alpha \\ \alpha &= \frac{6\pi}{18} \\ \alpha &= \frac{\pi}{3}\ \text{rad} \end{aligned}\]

Gabarito: A.

Conclusão

Para cunha esférica (setor esférico), memorize: \(A_{\text{fuso}}=2r^{2}\alpha\) e \(V_{\text{cunha}}=\dfrac{2\alpha}{3}r^{3}\) (com \(\alpha\) em rad). Em graus, substitua \(\alpha_{\text{rad}}=\alpha_{\text{graus}}\pi/180\). Essas relações aparecem muito em problemas de Geometria Espacial e no ENEM.