Você já entendeu intuitivamente o que é limite, observando gráficos ou tabelas de aproximação. Mas agora é hora de aprender a definição mais rigorosa — a chamada definição formal de limite, também conhecida como definição épsilon-delta (ε-δ).

Essa definição é a base do pensamento matemático preciso, utilizada em provas formais, na análise de funções e em aplicações práticas da matemática.

O que é o Limite de uma Função?

A ideia básica é simples: o limite de uma função f(x), quando x se aproxima de um número a, é o valor que f(x) tende a assumir à medida que x se aproxima de a.

Mesmo que f(x) não esteja definida exatamente no ponto x = a, o limite pode existir — desde que o comportamento da função perto de a seja previsível.

A Definição Épsilon-Delta (ε-δ)

A definição formal é a seguinte:

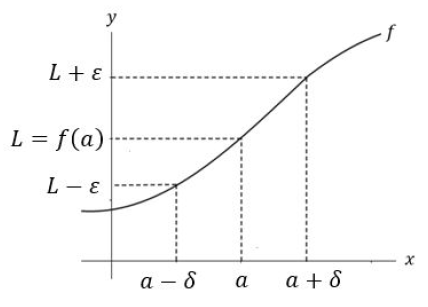
O limite de f(x) quando x tende a um número a é igual a L se, para todo número positivo ε (épsilon), por menor que seja, for possível encontrar um número positivo δ (delta) tal que:

Se 0 < |x – a| < δ, então |f(x) – L| < ε.

Ou seja, conseguimos controlar o quão perto f(x) chega de L, ajustando o quão perto x precisa estar de a.

Interpretação Visual

• Imagine o ponto x = a em uma reta numérica.
• Ao redor dele, traçamos um pequeno intervalo de raio δ.
• Agora, observamos f(x) e traçamos uma faixa ao redor do valor L, com largura ε.
• Se todos os valores de f(x), para x dentro do intervalo (sem incluir o ponto a), caem dentro da faixa de L, então o limite existe e é igual a L.

Notações Comuns

As notações mais utilizadas são:

• lim f(x) = L quando x → a — Lê-se: “o limite de f de x, quando x tende a a, é igual a L”.
• lim f(x) = ∞ quando x → a — Indica que os valores da função crescem sem limite (vão para infinito) quando x se aproxima de a.
• lim f(x) quando x → a⁻ — Limite lateral pela esquerda.
• lim f(x) quando x → a⁺ — Limite lateral pela direita.

Limites Laterais

1. Limite pela esquerda

É o valor que f(x) tende a assumir quando x se aproxima de a por valores menores que a.

Notação: lim f(x) = L quando x → a⁻

2. Limite pela direita

É o valor que f(x) tende a assumir quando x se aproxima de a por valores maiores que a.

Notação: lim f(x) = L quando x → a⁺

Quando o Limite Geral Existe?

O limite geral de f(x) em x = a existe se — e somente se — os dois limites laterais existem e são iguais.

Se:

• lim f(x) = L quando x → a⁻
• lim f(x) = L quando x → a⁺

Então:

• lim f(x) = L quando x → a

Se os dois limites laterais forem diferentes, então o limite em x = a não existe.

Exemplo de Limite Lateral

Considere a função:

f(x) = 
  1, se x < 0
  2, se x ≥ 0

Vamos calcular:

• Limite pela esquerda: Quando x se aproxima de 0 por valores menores, f(x) = 1 → então lim f(x) = 1 quando x → 0⁻.
• Limite pela direita: Quando x se aproxima de 0 por valores maiores, f(x) = 2 → então lim f(x) = 2 quando x → 0⁺.

Como os dois limites laterais são diferentes, o limite em x = 0 não existe.

A Unicidade do Limite

Um ponto importante: o limite, se existir, é único.

Isso significa que uma função não pode ter dois valores diferentes como limite no mesmo ponto. Se os limites laterais forem diferentes, o limite total não existe.

Por Que Isso é Importante?

• Garante rigor lógico ao estudo das funções.
• Serve de base para conceitos como continuidade e derivadas.
• Permite analisar o comportamento de funções em pontos com descontinuidade ou irregularidade.

Conclusão

A definição épsilon-delta de limite é o que dá ao Cálculo sua precisão matemática. Embora pareça abstrata no início, com prática ela se torna uma ferramenta extremamente útil e necessária.

Entender essa definição é o primeiro passo para dominar o Cálculo de forma profunda e segura, avançando para tópicos como derivadas, integrais e séries numéricas.

• Noção Intuitiva de Limites
• Definição Formal de Limite
• Limites Laterais
• Assíntotas Horizontais e Verticais
• Continuidade de Funções
• Limites no Infinito
• Limites Indeterminados