Calcular a distância entre um ponto e uma reta é uma daquelas habilidades que aparecem em provas de concurso, ENEM e na prática de quem estuda Geometria Analítica. Mesmo assim, muitos alunos ainda ficam inseguros na hora de aplicar a fórmula. Neste artigo completo, você vai entender como funciona o cálculo, por que ele é tão importante e como usá-lo de forma rápida e segura. O passo a passo está detalhado, com exemplos resolvidos, exercícios com respostas e ilustrações que facilitam o entendimento. .
Distância ponto–reta: definição e fórmula oficial
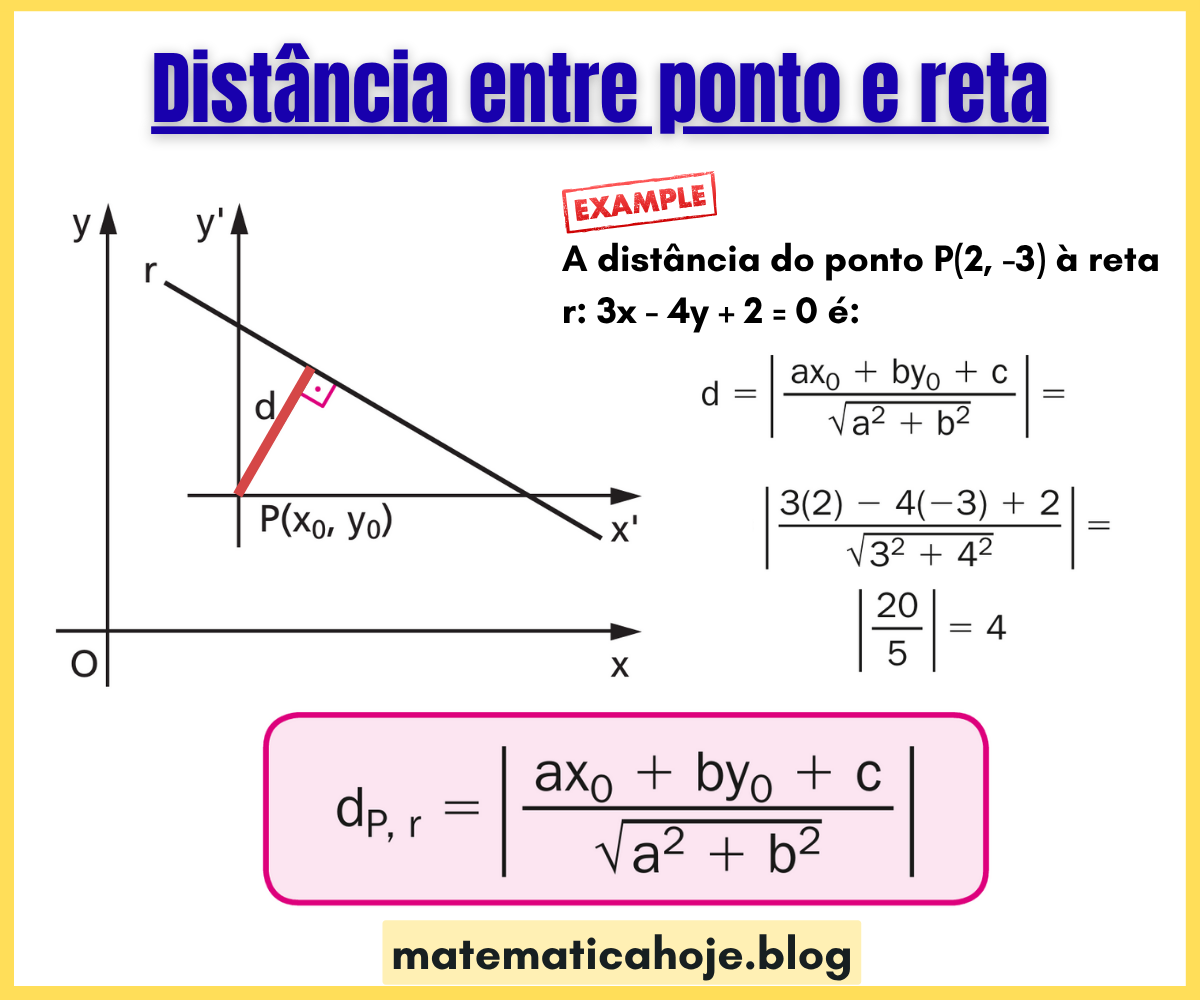
Quando você precisa medir o “menor caminho” entre um ponto \(P(x_0,y_0)\) e uma reta \(ax+by+c=0\), a resposta é a distância perpendicular entre eles. Essa medida é dada pela fórmula canônica:
O valor absoluto garante distância não-negativa. O denominador \(\sqrt{a^2+b^2}\) normaliza os coeficientes da reta; por isso, é importante usar a equação na forma \(ax+by+c=0\).
Tenha a fórmula da distância ponto-reta e muitas outras em um PDF bonito para consulta rápida.
Quero o eBook gratuitoExemplo resolvido: distância de ponto até uma reta
Enunciado. Qual é a distância do ponto \(P(2,-3)\) à reta \(3x-4y+2=0\)?
Ver solução
Identifique \(a=3\), \(b=-4\), \(c=2\) e \(x\_0=2\), \(y\_0=-3\).
\[ \begin{aligned} d \;&=\; \left|\,\frac{3\cdot 2 + (-4)\cdot(-3) + 2}{\sqrt{3^{2}+(-4)^{2}}}\,\right| \\ & =\; \left|\,\frac{6 + 12 + 2}{\sqrt{9+16}}\,\right| \\ & =\; \left|\,\frac{20}{\sqrt{25}}\,\right| \\ & =\; \left|\,\frac{20}{5}\,\right| \\ & =\; 4 \end{aligned} \]Resposta: \(d=4\) unidades.
Passo a passo seguro: como evitar erros comuns
- Coloque a reta exatamente na forma \(ax+by+c=0\) (nada de \(y=mx+n\) aqui).
- Use o sinal correto de \(b\) e de \(c\) ao substituir na fórmula.
- Não esqueça do valor absoluto para obter uma distância positiva.
- Depois das igualdades, escreva os cálculos um abaixo do outro para conferir cada etapa.
Guarde este conteúdo no seu caderno digital. Baixe o eBook gratuito com as fórmulas essenciais.
Baixar agoraMais exemplos resolvidos: distância ponto–reta na prática
Exemplo 1 — Substituição direta sem mistério
Enunciado. Encontre a distância do ponto \((3,1)\) até a reta \(x+2y-9=0\).
Ver solução
Se quiser racionalizar: \( \dfrac{4}{\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\).
Exemplo 2 — Cuidado com o sinal de \(b\)
Enunciado. Determine a distância do ponto \((-2,4)\) para a reta \(3x – y + 1 = 0\).
Ver solução (corrigida)
Aqui \(a=3\), \(b=-1\), \(c=1\). Substituindo corretamente:
\[ \begin{aligned} d \;&=\; \left|\,\frac{3(-2) + (-1)\cdot 4 + 1}{\sqrt{3^{2}+(-1)^{2}}}\,\right| \\ & =\; \left|\,\frac{-6 – 4 + 1}{\sqrt{9 + 1}}\,\right| \\ & =\; \left|\,\frac{-9}{\sqrt{10}}\,\right| \\ & =\; \frac{9}{\sqrt{10}} \end{aligned} \]Racionalizando: \( \dfrac{9}{\sqrt{10}} = \dfrac{9\sqrt{10}}{10}\).
Lista de exercícios com soluções passo a passo
Questão 1 — Distância ponto–reta direta
Enunciado. Calcule a distância do ponto \((0,-2)\) à reta \(2x+3y+6=0\).
Ver solução
O ponto pertence à reta, então a distância é zero.
Questão 2 — Ajuste para forma \(ax+by+c=0\)
Enunciado. Determine a distância do ponto \((5,1)\) à reta \(y=\tfrac12 x – 3\).
Ver solução
Leve para \(ax+by+c=0\): \(x – 2y – 6 = 0\) (\(a=1\), \(b=-2\), \(c=-6\)).
\[ \begin{aligned} d \;&=\; \left|\,\frac{1\cdot 5 + (-2)\cdot 1 + (-6)}{\sqrt{1^{2}+(-2)^{2}}}\,\right| \\ & =\; \left|\,\frac{5 – 2 – 6}{\sqrt{5}}\,\right| \\ & =\; \left|\,\frac{-3}{\sqrt{5}}\,\right| \\ & =\; \frac{3}{\sqrt{5}} \;=\; \frac{3\sqrt{5}}{5} \end{aligned} \]Questão 3 — Coeficiente \(b=0\)
Enunciado. Encontre a distância do ponto \((-1,4)\) à reta vertical \(x-3=0\).
Ver solução
A reta é \(1\cdot x + 0\cdot y – 3=0\). Então:
\[ \begin{aligned} d \;&=\; \left|\,\frac{1\cdot(-1) + 0\cdot 4 – 3}{\sqrt{1^{2}+0^{2}}}\,\right| \\ & =\; \left|\,\frac{-4}{1}\,\right| \\ & =\; 4 \end{aligned} \]Questão 4 — Coeficiente \(a=0\)
Enunciado. Determine a distância do ponto \((7,-5)\) à reta horizontal \(y+1=0\).
Ver solução
Forma: \(0\cdot x + 1\cdot y + 1=0\).
\[ \begin{aligned} d \;&=\; \left|\,\frac{0\cdot 7 + 1\cdot(-5) + 1}{\sqrt{0^{2}+1^{2}}}\,\right| \\ & =\; \left|\,\frac{-4}{1}\,\right| \\ & =\; 4 \end{aligned} \]Conclusão: como dominar distância ponto–reta
Para não errar: (1) coloque a reta em \(ax+by+c=0\); (2) substitua \((x\_0,y\_0)\) com atenção ao sinal de \(b\) e \(c\); (3) mantenha os cálculos “um embaixo do outro” usando a notação alinhada. Com prática — e com o apoio do eBook de fórmulas — você resolve qualquer questão em segundos.
Perguntas frequentes (FAQ)
Quando devo usar a fórmula da distância ponto–reta?
Use quando o enunciado pedir o menor caminho entre um ponto e uma reta no plano cartesiano. A distância é sempre medida de forma perpendicular à reta.
Preciso transformar a reta para \(ax+by+c=0\) sempre?
Sim. A fórmula oficial exige essa forma. Se estiver em \(y=mx+n\), leve os termos para o lado esquerdo até obter \(ax+by+c=0\).
O que acontece se eu esquecer o valor absoluto?
Você pode obter um número negativo, o que não faz sentido para distâncias. O valor absoluto corrige o sinal e garante um resultado não-negativo.
Posso racionalizar o denominador sem perder pontos?
Pode. Em provas, \(\tfrac{k}{\sqrt{n}}\) ou \(\tfrac{k\sqrt{n}}{n}\) costumam valer o mesmo. Siga o padrão pedido pela banca ou pelo professor.
Como revisar rápido antes da prova?
Guarde um mapa mental com a fórmula, dois exemplos resolvidos e uma lista curta de erros comuns. Refaça três exercícios cronometrados.













