A dízima periódica é um conceito fundamental no estudo dos números racionais e das frações. Ela está presente em diversos contextos matemáticos e tem uma importância significativa na compreensão dos números decimais e suas representações.
1. O Que é Dízima Periódica?
Uma dízima periódica é uma representação decimal de um número racional que possui um ou mais dígitos que se repetem indefinidamente. Esses dígitos repetitivos são chamados de período. A parte que antecede o período, se existir, é chamada de anteperíodo.
Exemplo:
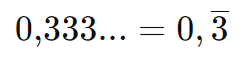
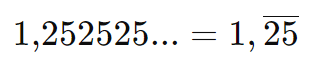
No primeiro exemplo, o dígito 3 é o período. No segundo exemplo, o grupo de dígitos 25 é o período.
2. Classificação das Dízimas Periódicas
As dízimas periódicas podem ser classificadas em dois tipos principais:
- Dízima periódica simples: Quando o período começa logo após a vírgula, sem que haja parte não periódica. Exemplo: (0,777…).
- Dízima periódica composta: Quando existe uma parte não periódica (anteperíodo) antes do início do período. Exemplo: (0,1232323…).
3. Como Identificar uma Dízima Periódica
Nem todos os números decimais são dízimas periódicas. A identificação é simples:
- Dízima periódica: Um número racional que, ao ser convertido para decimal, apresenta repetição infinita de um ou mais dígitos.
- Decimal exato: Um número racional que, ao ser convertido para decimal, possui um número finito de dígitos após a vírgula. Exemplo: (1/4 = 0,25).
4. Transformação de Dízima Periódica em Fração
Uma das propriedades mais interessantes das dízimas periódicas é a possibilidade de convertê-las em frações. O processo envolve alguns passos simples:
Exemplo 1: Convertendo 0,333… em Fração
- Seja x = 0,333…
- Multiplique ambos os lados da equação por 10 (uma potência de 10 que desloca o período):
10x = 3,333… - Subtraia a equação original da nova equação:
10x = 3,333… -(x = 0,333…) - Temos: 9x = 3
- Divida ambos os lados por 9:
x = 3/9 = 1/3
Portanto, 0,333… = 1/3.
Exemplo 2: Convertendo 0,1666…. em Fração
- Seja (x = 0,1666…).
- Multiplique ambos os lados por 10 para deslocar o anteperíodo:
10x=1,6666… - Multiplique ambos os lados por 10 novamente para deslocar o período:
100x=16,6666… - Subtraia a primeira equação da segunda:
100x=16,6666… -(10x=1,6666… ) - 90x=15
- Divida ambos os lados por 90:
x = 15/90 = 1/6
Portanto, x = 0,1666…= 1/6
Exemplo 3: Convertendo 0,212121…. em Fração
- Seja x = 0,212121….
- Multiplique ambos os lados da equação por 100 (uma potência de 100 que desloca o período):
100x=21,212121… - Subtraia a equação original da nova equação:
100x=21,212121… – (x = 0,212121….) - Temos: 99x=21
- Divida ambos os lados por 3:
x = 21/99 = 7/33
Portanto, 0,212121…. = 7/33.
Exemplo 4: Convertendo 0,212121…. em Fração
- Seja (x = 0,12444…).
- Multiplique ambos os lados por 1000 para deslocar o anteperíodo:
1000x=124,444… - Multiplique ambos os lados por 100 novamente para deslocar o período até o primeiro período do 4:
100x=12,444… - Subtraia a primeira equação da segunda:
1000x=124,44… -(100x=12,444… ) - 900x=112
- Divida ambos os lados por 4:
x = 112/900 = 28/225
Portanto, x = 0,12444… = 28/225
Exemplo 5: Convertendo 1,23333… em Fração
- Seja (x = 1,23333…).
- Multiplique ambos os lados por 100 para deslocar o anteperíodo:
100x=123,333… - Multiplique ambos os lados por 10 novamente para deslocar o período.
10x=12,333… - Subtraia a primeira equação da segunda:
100x=123,333… -(10x=12,333…) - 90x=111
- Divida ambos os lados por 3:
x = 111/90 = 37/30
Portanto, x = 1,23333… = 37/30
Dízima Periódica: Desafios e Soluções Detalhadas
5. Propriedades e Aplicações das Dízimas Periódicas
As dízimas periódicas são uma característica exclusiva dos números racionais. A periodicidade na representação decimal é uma evidência de que o número pode ser expresso como uma fração de dois inteiros.
Além disso, as dízimas periódicas têm aplicações práticas em diversas áreas, como:
- Computação: Na representação de números em sistemas de ponto flutuante.
- Engenharia: Em cálculos onde números racionais são usados em representações periódicas.
- Teoria dos Números: Na análise de padrões numéricos e suas propriedades.
6. Considerações Finais
A compreensão das dízimas periódicas é essencial para uma sólida formação matemática básica. Elas demonstram a conexão intrínseca entre frações e decimais e oferecem uma maneira poderosa de interpretar números racionais. A habilidade de converter entre dízimas periódicas e frações é uma ferramenta importante não só em matemática pura, mas também em aplicações práticas do dia a dia.
Ao explorar as dízimas periódicas, expandimos nossa visão sobre os números e suas representações, compreendendo melhor a beleza e a lógica por trás dos números racionais.