Domine a Trigonometria no Triângulo Retângulo com Exemplos Passo a Passo

Aprenda os principais conceitos de trigonometria no triângulo retângulo de forma prática e objetiva. Nesta lista, você encontrará questões resolvidas passo a passo, abordando seno, cosseno, tangente, aplicação do Teorema de Pitágoras e relações métricas. Ideal para reforçar o aprendizado e revisar conteúdos essenciais para provas, concursos e vestibulares.

Questão 1

Enunciado: Em cada caso, calcule o seno, o cosseno e a tangente do ângulo agudo destacado.

Questão 1 - Trigonometria

Questão 1 - Trigonometria

Solução Passo a Passo:

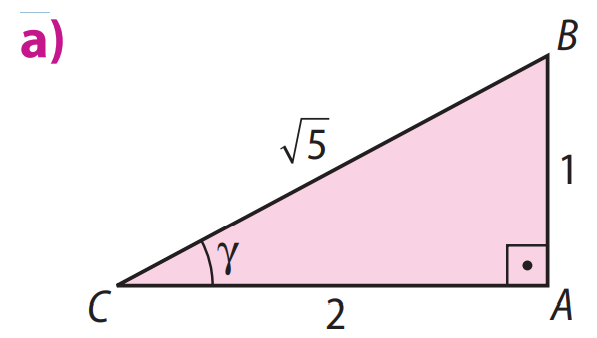
a) Para o triângulo \( \triangle CAB \) com o ângulo \( \gamma \):

\( \displaystyle sen \gamma = \frac{AB}{BC} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5} \)
\( \displaystyle \cos \gamma = \frac{AC}{BC} = \frac{2}{\sqrt{5}} = \frac{2\sqrt{5}}{5} \)
\( \displaystyle tg \gamma = \frac{AB}{AC} = \frac{1}{2} \)

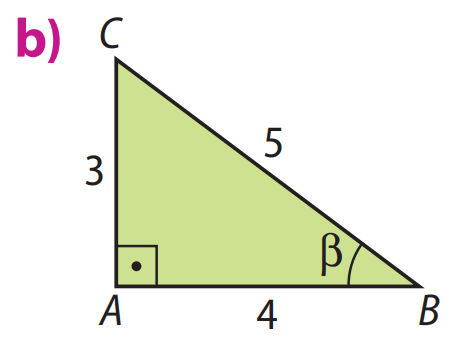
b) Para o triângulo \( \triangle ACB \) com o ângulo \( \beta \):

\( \displaystyle sen \beta = \frac{AC}{BC} = \frac{3}{5} \)
\( \displaystyle \cos \beta = \frac{AB}{BC} = \frac{4}{5} \)
\( \displaystyle tg \beta = \frac{AC}{AB} = \frac{3}{4} \)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 2

Enunciado: Retomando a situação da construção da rampa, a NBR 9050 estabelece que a inclinação deve ser calculada de acordo com a expressão:

\( i = \frac{h \cdot 100}{c} \)

em que:

  • i é a inclinação, em %;
  • h é a altura do desnível;
  • c é o comprimento da projeção ortogonal da rampa sobre o piso inferior.

Para desníveis de até 0,80 m, a inclinação permitida deve estar entre 6,25% e 8,33%.

Com base nessas informações, responda:

a) A expressão da inclinação pode ser relacionada com que razão trigonométrica? Justifique.

b) O que significa uma inclinação de 8%?

Solução Passo a Passo:

a) A expressão da inclinação está relacionada à razão trigonométrica tangente, pois em um triângulo retângulo formado pela rampa:

\(\tan \theta = \frac{\text{cateto oposto}}{\text{cateto adjacente}} = \frac{h}{c}\).

Logo, a inclinação \(i\) é diretamente proporcional a \(\tan \theta\), sendo:

\(i = \frac{h}{c} \cdot 100.\)

b) Uma inclinação de 8% significa que, para cada 100 unidades de comprimento horizontal, a rampa sobe 8 unidades na vertical:

\(\frac{h}{c} = \frac{8}{100} = 0{,}08.\)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 3

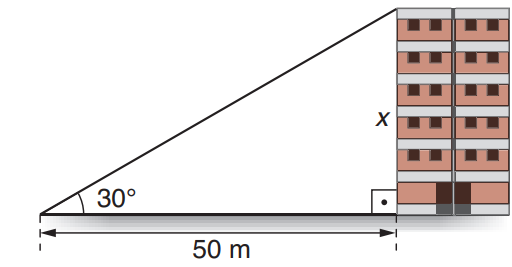
Enunciado: Quando os raios do sol formam o ângulo de \(30^\circ\) com o plano do chão, obtém-se a medida de 50 m para a sombra de um prédio. Qual é a altura aproximada desse prédio? Adote \(tg 30^\circ = 0{,}58.\)

Questão 3 - Altura do Prédio

Solução Passo a Passo:

Para determinar a altura \(x\) do prédio, utilizamos a relação da tangente no triângulo retângulo formado:

\(tg 30^\circ = \frac{x}{50}\)

Substituindo o valor de \(tg 30^\circ = 0{,}58\), temos:

\(0{,}58 = \frac{x}{50} \Rightarrow x = 0{,}58 \cdot 50 = 29 \, \text{m}\)

Portanto, a altura aproximada do prédio é 29 metros.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 4

Enunciado: Em um triângulo retângulo, um cateto mede 15 cm, e a hipotenusa, 17 cm. Calcule o seno, o cosseno e a tangente do maior ângulo agudo desse triângulo.

Solução Passo a Passo:

Primeiro, determinamos o outro cateto utilizando o Teorema de Pitágoras:

\(17^2 = x^2 + 15^2 \Rightarrow x^2 = 289 – 225 = 64 \Rightarrow x = 8 \, \text{cm}\)

Como 8 cm é o menor lado, o ângulo oposto a este cateto é o menor ângulo. Portanto, o maior ângulo agudo está oposto ao cateto de 15 cm.

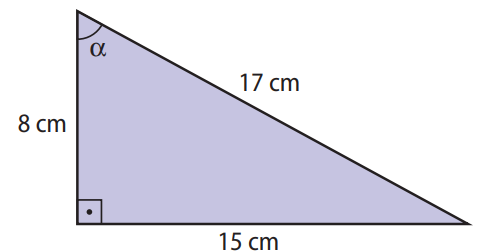
Questão 4 - Triângulo Retângulo

Assim, aplicando as definições de seno, cosseno e tangente, temos:

\(sen \alpha = \frac{15}{17}, \quad \cos \alpha = \frac{8}{17}, \quad tg \alpha = \frac{15}{8}\)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Regra de Três

Enunciado: Se 5 máquinas produzem 200 peças em 4 horas, quantas peças 8 máquinas produzirão no mesmo tempo?

Alternativas:

  • a) 300
  • b) 320
  • c) 340
  • d) 360

Solução Passo a Passo:

Se 5 máquinas produzem 200 peças, 1 máquina produz:

\( \frac{200}{5} = 40 \) peças.

Portanto, 8 máquinas produzirão:

\( 40 \cdot 8 = 320 \) peças.

Resposta correta: Letra B – 320 peças.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 5

Enunciado: Retomando a situação da introdução do capítulo, determine a altura \(h\) do barranco, sabendo que o teodolito está a 1,6 m do solo, alinhado com a base do barranco. Considere:

\(tg 41^\circ = 0,87 \quad \text{e} \quad tg 50^\circ = 1,19\)

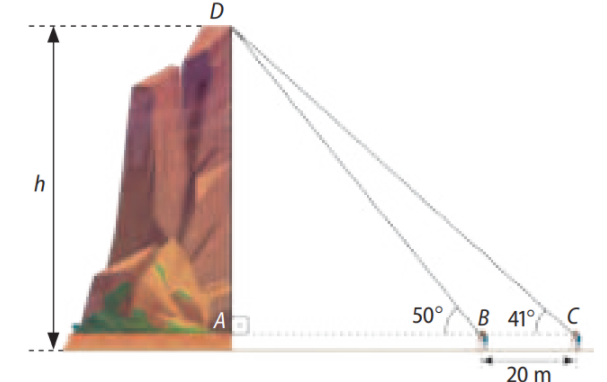
Questão 5 - Altura do Barranco

Solução Passo a Passo:

1. Triângulo ABD:

\(tg 50^\circ = \frac{h – 1,6}{AB} = 1,19 \Rightarrow h – 1,6 = 1,19 \cdot AB \tag{I}\)

2. Triângulo ADC:

\(tg 41^\circ = \frac{h – 1,6}{AB + 20} = 0,87 \Rightarrow h – 1,6 = 0,87 \cdot (AB + 20)\) \(\Rightarrow h – 1,6 = 0,87 \cdot AB + 17,4 \tag{II}\)

3. Sistema de Equações:

\(1,19 \cdot AB = 0,87 \cdot AB + 17,4\) \(0,32 \cdot AB = 17,4 \Rightarrow AB = \frac{17,4}{0,32} \approx 54,375\)

4. Altura do barranco:

\(h – 1,6 = 1,19 \cdot 54,375 \approx 64,71\) \(h = 64,71 + 1,6 = 66,31 \, \text{m}\)

Resposta: A altura aproximada do barranco é 66,31 m.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 6

Enunciado: Considere duas pessoas a 4 km de distância uma da outra, localizadas em dois pontos \(A\) e \(B\) no solo. A pessoa no ponto \(A\), olhando na direção de \(B\), avistou, segundo um ângulo de \(50^\circ\) com a horizontal, um helicóptero. No mesmo instante, a pessoa no ponto \(B\), olhando na direção de \(A\), avistou o mesmo helicóptero segundo um ângulo de \(45^\circ\) com a horizontal. Aproximadamente, a que altura do solo o helicóptero estava naquele momento? Considere:

\(sen 45^\circ = \cos 45^\circ \quad \text{e} \quad tg 50^\circ \approx 1,19\)

Solução Passo a Passo:

Seja \(h\) a altura do helicóptero e \(x\) a distância do ponto \(A\) à projeção vertical do helicóptero no solo. Então:

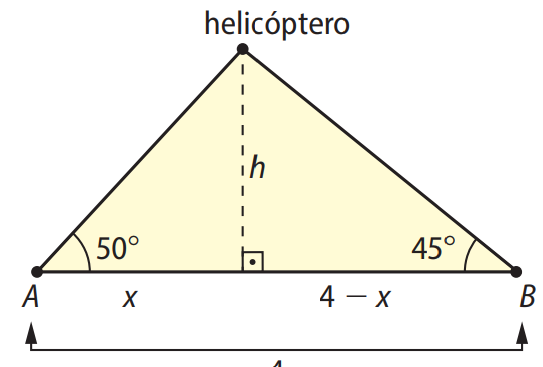
Questão 6 - Altura do Helicóptero

\(tg 45^\circ = \frac{h}{4 – x} \Rightarrow 1 = \frac{h}{4 – x} \Rightarrow h = 4 – x \Rightarrow x = 4 – h\)

Para o ponto \(A\), temos:

\(tg 50^\circ = \frac{h}{x} \Rightarrow 1,19 = \frac{h}{4 – h}\)

Resolvendo:

\(1,19 (4 – h) = h \Rightarrow 4,76 – 1,19h = h \Rightarrow 4,76 = 2,19h \Rightarrow h \approx 2,17 \, \text{km}\)

Resposta: A altura aproximada do helicóptero é 2,17 km ou 2.170 m.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 7

Enunciado: (Vunesp-SP) Um ciclista sobe, em linha reta, uma rampa com inclinação de \(3^\circ\) a uma velocidade constante de 4 m/s.

Questão 7 - Movimento em Rampa

A altura do topo da rampa em relação ao ponto de partida é de 30 m. Use a aproximação \(sen 3^\circ \approx 0,05\) e responda: O tempo, em minutos, que o ciclista levou para percorrer completamente a rampa foi:

Alternativas:

  • a) 2,5
  • b) 7,5
  • c) 10
  • d) 15
  • e) 30

Solução Passo a Passo:

Primeiro, calculamos o comprimento \(x\) da rampa (hipotenusa):

\(sen 3^\circ = \frac{30}{x} \Rightarrow 0,05 = \frac{30}{x} \Rightarrow x = \frac{30}{0,05} = 600 \, \text{m}\)

Com a distância percorrida \(x\), usamos a fórmula da velocidade para encontrar o tempo \(t\) (em segundos):

\(v = \frac{d}{t} \Rightarrow 4 = \frac{600}{t} \Rightarrow t = \frac{600}{4} = 150 \, \text{s}\)

Convertendo para minutos:

\(t = \frac{150}{60} = 2,5 \, \text{minutos}\)

Resposta: Alternativa a) 2,5 minutos.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 8

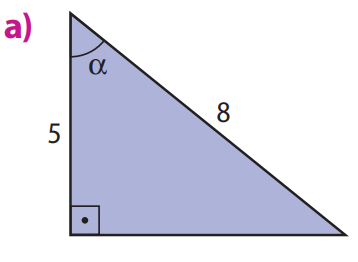
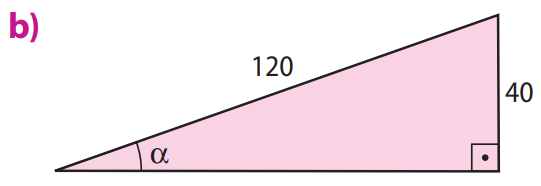
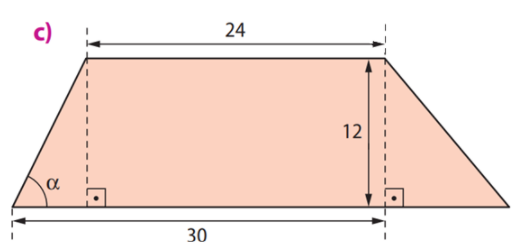
Enunciado: Determine a medida aproximada, em grau, do ângulo \(\alpha\) de cada figura. Utilize uma calculadora científica.

Questão 8 - Ângulos

Questão 8 - Ângulos

Questão 8 - Ângulos

Solução Passo a Passo:

a) No triângulo retângulo, temos:

\(\cos \alpha = \frac{5}{8} = 0,625 \Rightarrow \alpha \approx \cos^{-1}(0,625) \approx 51^\circ\)

b) No triângulo, usamos o seno:

\(sen \alpha = \frac{40}{120} = 0,333 \Rightarrow \alpha \approx sen^{-1}(0,333) \approx 19^\circ\)

c) No trapézio, primeiramente encontramos as medidas auxiliares:

\(AF = 30 – 24 = 6\)

Agora, a tangente de \(\alpha\) é:

\(tg \alpha = \frac{12}{6} = 2 \Rightarrow \alpha \approx tg^{-1}(2) \approx 63^\circ\)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 9

Enunciado: Considerando:

\(sen 10^\circ = 0,17,\; sen 65^\circ = 0,90,\; \cos 50^\circ = 0,64\)

Calcule:

  • a) \(\cos 25^\circ\)
  • b) \(\cos 80^\circ\)
  • c) \(sen 40^\circ\)

Solução Passo a Passo:

Utilizando a relação entre seno e cosseno, sabemos que \(\cos \theta = sen (90^\circ – \theta)\).

Assim:

a) \(\cos 25^\circ = sen 65^\circ = 0,90\)

b) \(\cos 80^\circ = sen 10^\circ = 0,17\)

c) \(sen 40^\circ = \cos 50^\circ = 0,64\)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 10

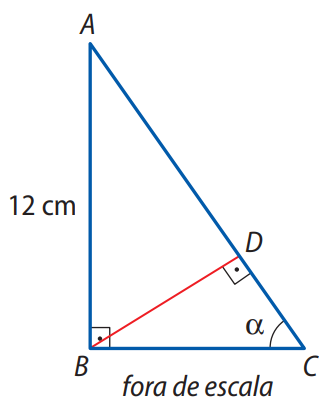
Enunciado: (UEA-AM) A figura mostra os triângulos retângulos \(ABC\) e \(BCD\), em que \(AB = 12 \, \text{cm}\) e \(\angle B\hat{C}D = \alpha\). Sabendo que \(sen \alpha = 0,8\) e que o ponto \(D\) está sobre o lado \(AC\), determine a medida do segmento \(DC\).

Questão 10 - Triângulos

Alternativas:

  • a) 5,4 cm
  • b) 3,6 cm
  • c) 4,5 cm
  • d) 6,3 cm
  • e) 7,2 cm

Solução Passo a Passo:

1. Determinar \(AC\) usando o seno:

\(sen \alpha = \frac{12}{AC} \Rightarrow 0,8 = \frac{12}{AC} \Rightarrow AC = \frac{12}{0,8} = 15 \, \text{cm}\)

2. Determinar \(BC\) usando Pitágoras no triângulo \(ABC\):

\(BC = \sqrt{AC^2 – AB^2} = \sqrt{15^2 – 12^2} = \sqrt{225 – 144} = \sqrt{81} = 9 \, \text{cm}\)

3. Determinar \(BD\) usando seno no triângulo \(BDC\):

\(sen \alpha = \frac{BD}{BC} \Rightarrow 0,8 = \frac{BD}{9} \Rightarrow BD = 0,8 \cdot 9 = 7,2 \, \text{cm}\)

4. Determinar \(DC\) com Pitágoras no triângulo \(BDC\):

\(DC = \sqrt{BC^2 – BD^2} = \sqrt{9^2 – 7,2^2} = \sqrt{81 – 51,84} = \sqrt{29,16} \approx 5,4 \, \text{cm}\)

Resposta: Alternativa a) 5,4 cm.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 11

Enunciado: A soma dos comprimentos das bases de um trapézio retângulo vale 30 m. A base maior mede o dobro da menor. Calcule a altura do trapézio, sabendo que seu ângulo obtuso mede \(150^\circ\). Considere \(sen 30^\circ = 0,5.\)

Solução Passo a Passo:

1. Determinar as bases:

Seja \(x\) o valor da menor base. A base maior é \(2x\) e:

\(x + 2x = 30 \Rightarrow 3x = 30 \Rightarrow x = 10 \, \text{m}\)

Logo, as bases são 10 m e 20 m.

2. Determinar a altura usando o ângulo de \(30^\circ\):

No triângulo retângulo formado, temos:

\(tg 30^\circ = \frac{h}{10} \Rightarrow \frac{\sqrt{3}}{3} = \frac{h}{10} \Rightarrow h = \frac{10 \sqrt{3}}{3} \, \text{m}\)

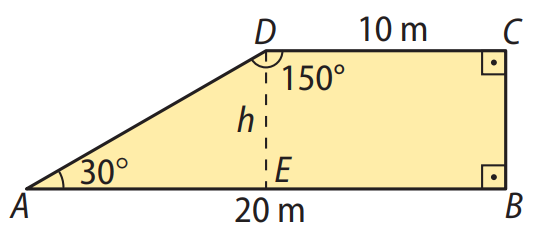
Questão 11 - Trapézio

Resposta: A altura do trapézio é \(\frac{10 \sqrt{3}}{3} \, \text{m}\).

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 12

Enunciado: (UECE) Um cabo de aço, medindo \(c\) metros de comprimento, é estendido em linha reta fixado em três pontos, a saber: \(P\) e \(Q\) em seus extremos e \(M\) em um ponto intermediário. O ponto \(P\) está localizado no solo plano horizontal e os pontos \(M\) e \(Q\) estão localizados no alto de duas torres erguidas verticalmente no mesmo solo. As medidas, em metros, das alturas das torres e a distância entre elas são, respectivamente, \(h\), \(H\) e \(d\). Se \(x\) é a medida em graus do ângulo que o cabo faz com o solo, a diferença entre a altura da torre maior e a da menor é:

Alternativas:

  • a) \( c \cdot tg (x) \)
  • b) \( d \cdot tg (x) \)
  • c) \( \frac{c \cdot h}{H} tg (x) \)
  • d) \( \frac{d \cdot h}{H} tg (x) \)

Solução Passo a Passo:

Considerando o triângulo \(AQM\), a tangente de \(x\) é dada por:

\(tg x = \frac{H – h}{d}\)

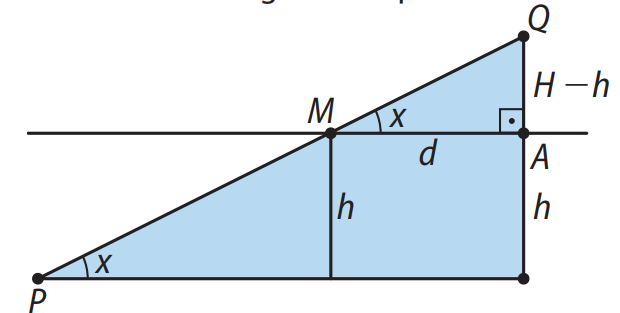
Questão 12 - Diferença de Alturas

Assim, a diferença entre as alturas das torres é:

\(H – h = d \cdot tg x\)

Resposta: Alternativa b) \( d \cdot tg (x) \).

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 13

Enunciado: Uma pessoa, distante 10 m de um prédio, observa o topo dele sob um ângulo de \(58^\circ\). Ao afastar-se desse prédio, ainda observa o topo sob um ângulo de \(22^\circ\). Calcule a altura do prédio e a distância de afastamento entre os pontos de observação. Considere: \(tg 22^\circ = 0,4\) e \(tg 58^\circ = 1,6.\)

Solução Passo a Passo:

1. Calcular a altura do prédio (\(h\)) usando o primeiro ponto de observação:

\(tg 58^\circ = \frac{h}{10} \Rightarrow 1,6 = \frac{h}{10} \Rightarrow h = 16 \, \text{m}\)

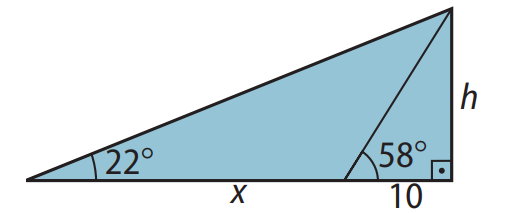
Questão 13 - Altura de Prédio

2. Determinar a distância (\(x\)) usando o segundo ponto de observação:

\(tg 22^\circ = \frac{h}{x + 10} \Rightarrow 0,4 = \frac{16}{x + 10} \Rightarrow x + 10 = \frac{16}{0,4} = 40 \Rightarrow x = 30 \, \text{m}\)

Resposta: A altura do prédio é 16 m e a distância entre os pontos de observação é 30 m.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Questão 14

Enunciado: Um submarino \(A\), que se encontra a uma profundidade de \(400 \, m\) no mar, detecta dois barcos \(B\) e \(C\) na superfície da água sob ângulos de \(62^\circ\) e \(40^\circ\), respectivamente, medidos entre a direção dos barcos e a direção perpendicular à superfície. Qual é a distância aproximada entre os dois barcos? Adote: \(tg 62^\circ = 1,9\) e \(tg 40^\circ = 0,8.\)

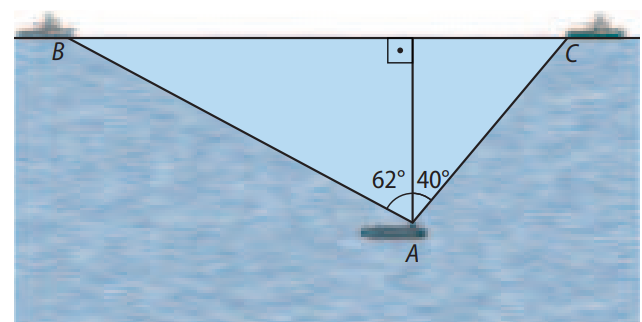
Questão 14 - Distância entre Barcos

Solução Passo a Passo:

1. Distância horizontal do submarino \(A\) ao barco \(B\):

\(tg 62^\circ = \frac{x}{400} \Rightarrow x = 1,9 \cdot 400 = 760 \, \text{m}\)

2. Distância horizontal do submarino \(A\) ao barco \(C\):

\(tg 40^\circ = \frac{y}{400} \Rightarrow y = 0,8 \cdot 400 = 320 \, \text{m}\)

3. Distância total entre os barcos:

\(d = x + y = 760 + 320 = 1080 \, \text{m}\)

Resposta: A distância entre os dois barcos é aproximadamente 1080 m.

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Relacionadas

Geometria Plana – Diferença de Perímetros com Arco de Circunferência

Matemática para Concursos: Geometria Plana – Banca VUNESP - Nível Médio

Geometria Plana – Ângulo entre segmentos (FGV – TRT 24ª Região – 2025)

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube
Rolar para cima