Nesta questão de Geometria Analítica do ENEM 2025, o cenário envolve um jogo digital com três personagens: um herói e dois vilões. O herói sempre será atacado pelo vilão que estiver mais próximo. Para evitar o ataque, ele deve se deslocar por uma trajetória que o mantenha equidistante dos dois vilões.
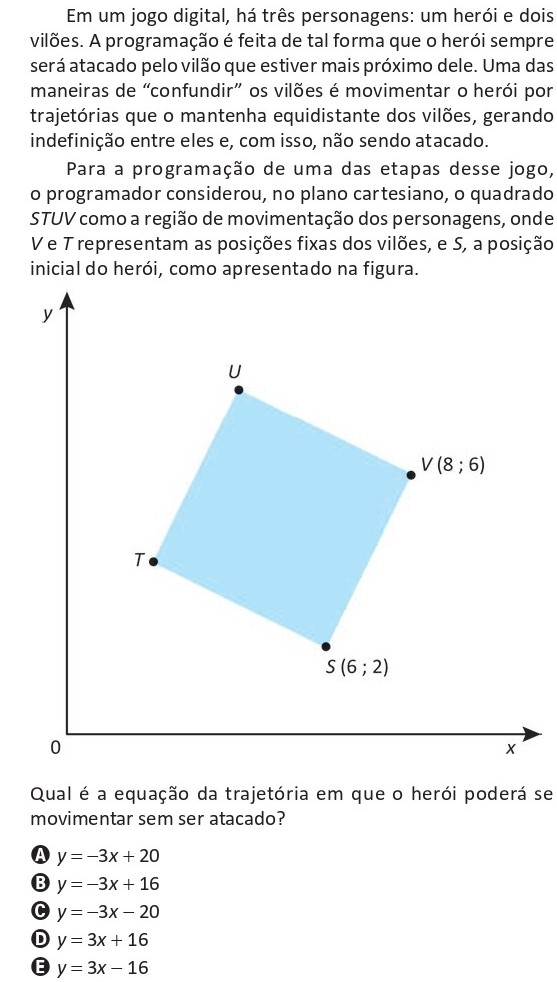
No plano cartesiano, o quadrado STUV representa a região de movimentação dos personagens. Os pontos V e T são as posições fixas dos vilões, e o ponto S indica a posição inicial do herói.
✅ Clique para ver a solução passo a passo
1) Coordenadas dos pontos do problema
- Vilão em V(8, 6)
- Vilão em T(2, 4)
- Herói em S(6, 2)
O herói deve se mover pela mediatriz do segmento VT, pois essa é a reta formada pelos pontos que estão à mesma distância de V e de T.
2) Cálculo do ponto médio de VT
M = ( (8 + 2)/2 , (6 + 4)/2 )
M = (10/2 , 10/2)
M = (5 , 5)
3) Coeficiente angular da reta VT
mVT = (6 − 4)/(8 − 2)
mVT = 2/6 = 1/3
Como a mediatriz é perpendicular à reta VT, seu coeficiente angular é o oposto do inverso:
m = −3
4) Equação da mediatriz
Usando a forma da equação da reta:
y − 5 = −3(x − 5)
y − 5 = −3x + 15
y = −3x + 20
5) Verificação do ponto S(6,2)
y = −3·6 + 20
y = −18 + 20
y = 2
Como o valor encontrado é exatamente 2, o ponto S(6,2) pertence à reta, confirmando que a equação está correta.
✅ Equação da trajetória segura do herói: y = −3x + 20
✅ Alternativa correta: A
Antes desta questão, resolvemos uma situação de Probabilidade envolvendo a devolução aleatória de celulares a candidatos de um concurso. Acesse a resolução completa em: ENEM 2025 – Probabilidade dos celulares .
Para continuar seus estudos com material organizado:
🔎 Veja mais resoluções completas do ENEM 2025:
https://matematicahoje.blog/category/matematica-enem-2025/













