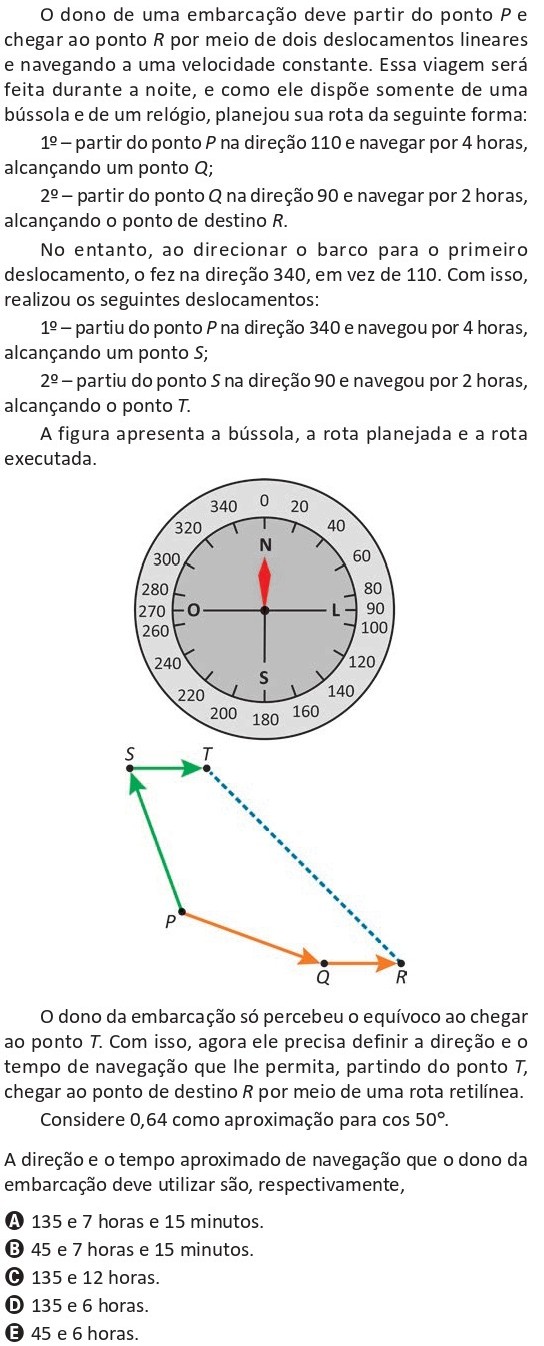
Nesta questão de Trigonometria e Vetores do ENEM 2025, o dono de uma embarcação precisa sair do ponto P e chegar ao ponto R, seguindo deslocamentos em direções medidas em graus na bússola e mantendo velocidade constante.
A rota planejada era:
- 1º: seguir de P na direção 110° por 4 horas, chegando a Q;
- 2º: seguir de Q na direção 90° por 2 horas, chegando a R.
Porém, por engano, o barco seguiu na direção 340° em vez de 110° no primeiro trecho, indo parar em S, e depois, na direção 90° por 2 horas, chegou ao ponto T.
Ao perceber o erro em T, o dono da embarcação precisa agora definir:
- a nova direção (em graus na bússola);
- e o tempo de navegação necessário para ir de T até o destino R em linha reta.
O enunciado ainda pede que se considere cos 50° ≈ 0,64.
✅ Clique para ver a solução passo a passo
1) Igualando velocidade e transformando em medida de distância
Como a embarcação navega com velocidade constante, podemos tomar essa velocidade como unidade. Assim:
- em 4 horas, o barco percorre um trecho de comprimento 4 unidades;
- em 2 horas, percorre um trecho de 2 unidades.
Logo, em qualquer rota:
- PQ = 4, QR = 2 (rota planejada);
- PS = 4, ST = 2 (rota executada).
2) Usando um sistema de eixos para representar os deslocamentos
Vamos adotar um sistema de coordenadas em que:
- o eixo vertical aponta para o Norte (N);
- o eixo horizontal aponta para o Leste (L);
- os ângulos da bússola são medidos a partir do Norte, no sentido horário.
Em termos de componentes, um deslocamento de comprimento d com direção θ terá:
(d · sen θ, d · cos θ)
Tomemos o ponto P como origem (0, 0) e consideremos a velocidade igual a 1 unidade/hora.
Rota planejada:
- PQ: direção 110°, comprimento 4 ⇒ PQ ≈ (4·sen110°, 4·cos110°)
- QR: direção 90°, comprimento 2 ⇒ QR = (2, 0)
Somando os vetores, obtemos as coordenadas aproximadas de R.
Rota executada:
- PS: direção 340°, comprimento 4 ⇒ PS ≈ (4·sen340°, 4·cos340°)
- ST: direção 90°, comprimento 2 ⇒ ST = (2, 0)
Somando, obtemos as coordenadas aproximadas de T.
3) Vetor de T até R
Fazendo os cálculos (usando aproximações usuais para senos e cossenos), encontramos:
- R ≈ (5,76 ; −1,37)
- T ≈ (0,63 ; 3,76)
Assim, o vetor TR é:
TR = R − T ≈ (5,76 − 0,63 ; −1,37 − 3,76) TR ≈ (5,13 ; −5,13)
Note que os módulos das componentes são iguais e os sinais indicam:
- Δx > 0 → deslocamento para o Leste;
- Δy < 0 → deslocamento para o Sul.
Ou seja, o barco deve seguir aproximadamente na direção Sudeste, fazendo com o Norte um ângulo de cerca de 135° (90° até o Leste + 45° para descer em direção ao Sul).
✔ Direção ≈ 135°
4) Comprimento de TR e tempo de navegação
O comprimento de TR é:
|TR| = √(5,13² + 5,13²) ≈ 5,13·√2 ≈ 7,25 (unidades de distância)
Como tomamos a velocidade igual a 1 unidade de distância por hora, o módulo do vetor TR é também o tempo necessário em horas:
Tempo ≈ 7,25 h
E
0,25 h = 0,25 · 60 min = 15 min
✅ Tempo aproximado de navegação: 7 horas e 15 minutos
✅ Direção aproximada: 135° (rumo Sudeste).
✅ Alternativa correta: A) 135 e 7 horas e 15 minutos.
Observação: a aproximação cos 50° ≈ 0,64, fornecida no enunciado, pode ser usada em uma abordagem por Lei dos Cossenos no triângulo formado pelos pontos P, T e R, chegando aos mesmos valores aproximados.
Na questão anterior, você trabalhou com Estatística e interpretação de gráficos sobre modalidades esportivas no ensino médio. Confira ou revise em: ENEM 2025 – Estatística: gráficos e quantidade total de alunos .
Para aprofundar seus estudos em Trigonometria, Geometria Analítica e demais tópicos de Matemática para o ENEM, aproveite os materiais organizados no Matemática Hoje:
🔎 Veja mais resoluções de Matemática do ENEM 2025 em:
https://matematicahoje.blog/category/matematica-enem-2025/

























