Equação da Reta — Guia Completo com Exemplos
Entenda as formas da equação da reta, como calcular o coeficiente angular e como montar a reta a partir de um ponto, dois pontos ou da inclinação.
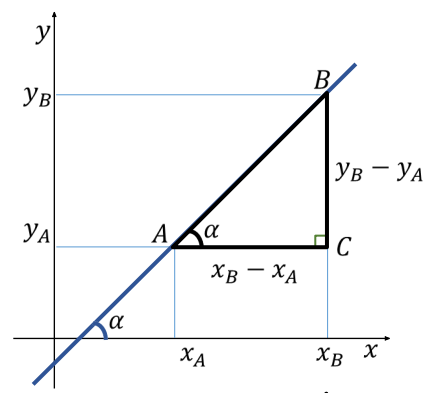
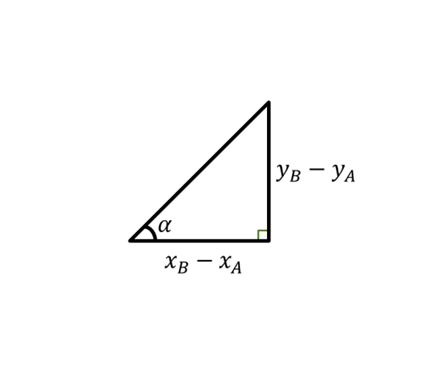
1) Conceito e interpretação geométrica
Uma reta é o conjunto de pontos do plano que satisfazem uma relação linear entre \(x\) e \(y\). A inclinação \(m\) mede a variação vertical por unidade de variação horizontal:
\(m=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}\)
Dica: Se \(m>0\) a reta é crescente; se \(m<0\), decrescente. Retas paralelas têm o mesmo \(m\); perpendiculares satisfazem \(m_1\cdot m_2=-1\) (quando ambos definidos).
2) Formas da equação da reta
2.1 Forma reduzida (inclinação–intercepto)
\(y=mx+n\)
\(m\) é a inclinação e \(n\) é a interseção com o eixo \(y\) (ordenada na origem).
2.2 Forma ponto–inclinação
\(y-y_0=m(x-x_0)\)
Conhecendo \(m\) e um ponto \(P_0(x_0,y_0)\), obtemos a reta rapidamente.
2.3 Forma a partir de dois pontos
\(y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)\)
Útil quando temos apenas dois pontos da reta.
2.4 Forma geral
\(ax+by+c=0\)
Boa para verificar paralelismo e perpendicularidade de modo algébrico.
3) Construções práticas
3.1 A partir de \(m\) e de um ponto
Se \(m\) e \(P_0(x_0,y_0)\) são conhecidos, use \(y-y_0=m(x-x_0)\) e, se desejar, isole \(y\) para obter \(y=mx+n\).
3.2 A partir de dois pontos
- Calcule \(m=\dfrac{y_2-y_1}{x_2-x_1}\).
- Substitua em \(y-y_1=m(x-x_1)\) e simplifique.
3.3 Convertendo para a forma geral
Reorganize a expressão para \(ax+by+c=0\) multiplicando e somando termos adequadamente.
4) Exemplos resolvidos
Exemplo 1 — Reta por dois pontos \(A(1,2)\) e \(B(5,6)\)
Passo 1: \(m=\dfrac{6-2}{5-1}=\dfrac{4}{4}=1.\)
Passo 2: Com \(m=1\) e o ponto \(A(1,2)\): \(y-2=1(x-1)\Rightarrow y=x+1.\)
Forma geral: \(x-y+1=0.\)
Exemplo 2 — Reta com \(m=-\tfrac{3}{2}\) que passa por \(P_0(4,-1)\)
Passo 1: Use a forma ponto–inclinação: \(y+1=-\tfrac{3}{2}(x-4).\)
Passo 2 (reduzida): \(y=-\tfrac{3}{2}x+6-1=-\tfrac{3}{2}x+5.\)
Forma geral: \(3x+2y-10=0.\)
5) Exercícios propostos
- Encontre a equação da reta que passa por \(C(2,-5)\) e \(D(-4,7)\) nas formas reduzida e geral.
- Determine a equação da reta paralela a \(3x-2y+8=0\) que passa por \(P(1,1)\).
- Encontre a reta perpendicular a \(y=\tfrac{1}{3}x-4\) que passa por \(Q(0,2)\).
- Dada a reta \(ax+by+c=0\) com \(a=4\), \(b=-3\) e que passa por \((1,2)\), calcule \(c\) e escreva a forma reduzida.
👀 Gabarito (resumos)
1) \(m=\dfrac{7-(-5)}{-4-2}=\dfrac{12}{-6}=-2\Rightarrow y+5=-2(x-2)\Rightarrow y=-2x-1;\; 2x+y+1=0.\)
2) Paralela \(\Rightarrow m=\tfrac{3}{2}\). Ponto \(P(1,1)\): \(y-1=\tfrac{3}{2}(x-1)\Rightarrow y=\tfrac{3}{2}x-\tfrac{1}{2}.\)
3) Perpendicular a \(m=\tfrac{1}{3}\Rightarrow m’=-3\). \(y-2=-3(x-0)\Rightarrow y=-3x+2.\)
4) \(4(1)-3(2)+c=0\Rightarrow 4-6+c=0\Rightarrow c=2\). Logo \(4x-3y+2=0\Rightarrow y=\tfrac{4}{3}x+\tfrac{2}{3}.\)
6) Conexões úteis
- Função do 1º Grau — relação direta com a forma \(y=mx+n\).
- Geometria Analítica — distância entre pontos, ponto médio, circunferência.
- Reta Tangente & Derivada — ligação entre inclinação e taxa de variação.
Equação da Reta — Lista Interativa (10 questões)
Clique em uma alternativa para verificar imediatamente se está correta. Em seguida, use o botão Ver solução para ver o passo a passo (estilo: azul fechado / verde aberto).
1) Coeficiente angular
Determine o coeficiente angular da reta que passa pelos pontos \(A(2,3)\) e \(B(5,9)\).
👀 Ver solução passo a passo
2) Equação da reta por dois pontos
Encontre a equação da reta que passa por \(P(1,2)\) e \(Q(4,8)\).
👀 Ver solução passo a passo
3) Coeficiente linear
Determine o coeficiente linear da reta \(3x-4y+12=0\).
👀 Ver solução passo a passo
4) Equação reduzida
Determine a equação da reta com coeficiente angular \(m=-2\) que passa por \((3,5)\).
👀 Ver solução passo a passo
5) Equação geral por dois pontos
Obtenha a equação geral da reta que passa por \(A(-1,4)\) e \(B(3,-2)\).
👀 Ver solução passo a passo
6) Ponto pertence à reta?
Verifique se o ponto \(P(2,-1)\) pertence à reta \(2x+3y-4=0\).
👀 Ver solução passo a passo
7) Reta paralela
Determine a equação da reta paralela a \(3x-2y+5=0\) que passa por \(P(2,-1)\).
👀 Ver solução passo a passo
8) Reta perpendicular
Encontre a equação da reta perpendicular a \(2x+y-6=0\) que passa por \(Q(4,-2)\).
👀 Ver solução passo a passo
9) Distância ponto–reta
Calcule a distância do ponto \(P(3,5)\) até a reta \(x+2y-8=0\).
👀 Ver solução passo a passo
10) Reta tangente à parábola
Determine a equação da reta tangente à parábola \(y=x^2\) no ponto \(T(2,4)\).













