As equações do segundo grau são um dos tópicos mais fundamentais da álgebra, encontradas em diversas áreas da matemática e ciências aplicadas. Neste artigo, vamos explorar profundamente todos os aspectos das equações do segundo grau, desde sua definição básica até suas aplicações práticas, passando por métodos de resolução e curiosidades matemáticas.
O que é uma Equação do Segundo Grau?
Uma equação do segundo grau é uma equação polinomial de grau 2, o que significa que a maior potência da variável é 2. A forma geral de uma equação do segundo grau em uma variável (x) é:
ax2 + bx + c = 0
onde:
- a, b, e c são coeficientes reais (ou complexos), e
- a ≠ 0 para que a equação seja de fato do segundo grau.
Se a = 0, a equação se torna linear, ou seja, uma equação de primeiro grau.
Exemplos de Equações do Segundo Grau
- 2x2 + 3x – 5 = 0
- x2 – 4x + 4 = 0
- -x2 + 6x + 8 = 0
Cada uma dessas equações possui uma forma quadrática, e a resolução delas nos leva a encontrar as raízes da equação.
Raízes da Equação do Segundo Grau
As raízes de uma equação do segundo grau são os valores de x que satisfazem a equação, ou seja, que tornam a equação verdadeira. Dependendo dos coeficientes a, b e c, uma equação do segundo grau pode ter:
- Duas raízes reais e distintas,
- Uma raiz real dupla,
- Ou duas raízes complexas conjugadas.
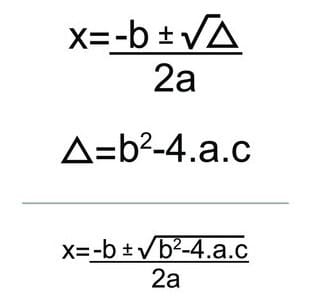
A fórmula geral para encontrar as raízes de uma equação do segundo grau é dada pela famosa Fórmula de Bhaskara:
O Discriminante
O discriminante de uma equação do segundo grau é a expressão (Delta ∆) ∆ = b2 – 4ac , e é ele que determina a natureza das raízes:
- Se ( ∆ > 0 ): A equação tem duas raízes reais e distintas.
- Se ( ∆ = 0 ): A equação tem uma raiz real dupla (também chamada de raiz repetida).
- Se ( ∆ < 0 ): A equação não tem raízes reais ou tem duas raízes complexas conjugadas.
Exemplos de Resolução
Vamos resolver a equação 2x2 + 3x – 5 = 0 usando a Fórmula de Bhaskara.
- Identificamos os coeficientes: a = 2, b = 3, c = -5.
- Calculamos o discriminante:
Δ= 32−4⋅2⋅(−5) = 9+40 = 49 - Como Δ>0, sabemos que há duas raízes reais e distintas.
- Calculamos as raízes usando a Fórmula de Bhaskara:
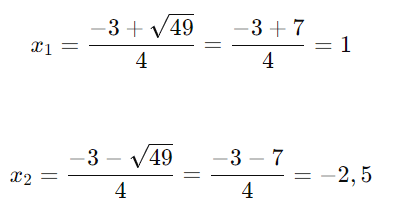
As raízes da equação são x1 = 1 e x2 = -2,5.
Exercícios Equação do Segundo grau
Exercício 1
Enunciado: Resolva a equação 2x2 − 4x − 6 = 0 utilizando a fórmula de Bhaskara.
olução:
Dada a equação 2x2 − 4x − 6 = 0, identificamos os coeficientes:
- a=2
- b=−4
- c=−6
A fórmula de Bhaskara é dada por:
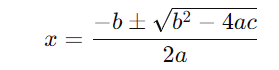
Vamos calcular o discriminante (Δ):
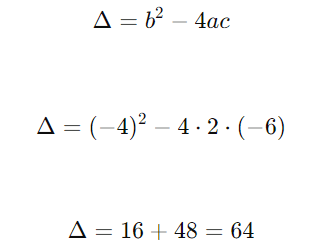
Agora, substituímos na fórmula de Bhaskara:
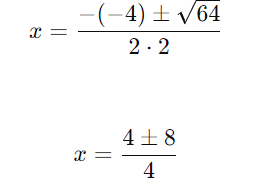
As raízes são:
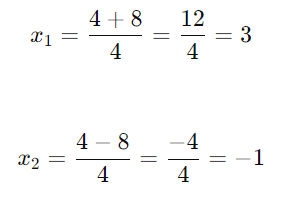
Resposta: As soluções são x1=3 e x2=−1
Exercício 2
Enunciado: Resolva a equação x2 − 6x + 9 = 0.
Solução:
Dada a equação x2 − 6x + 9 = 0, temos:
- a=1
- b=−6
- c=9
Vamos calcular o discriminante (Δ):
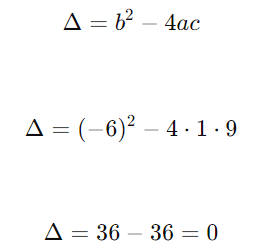
Como o discriminante é zero, a equação tem uma raiz real dupla:
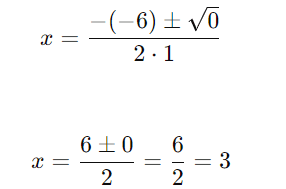
Resposta: A solução é x = 3 (raiz dupla).
Exercício 3
Enunciado: Resolva a equação 3x2 + 7x + 2 = 0.
Solução:
Para a equação 3x2 + 7x + 2 = 0, temos:
- a=3
- b=7
- c=2
Calculando o discriminante Δ:
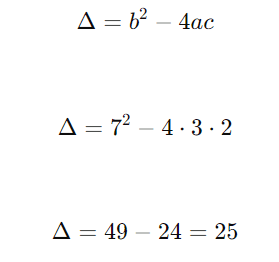
Substituindo na fórmula de Bhaskara:
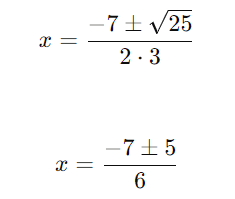
As raízes são:
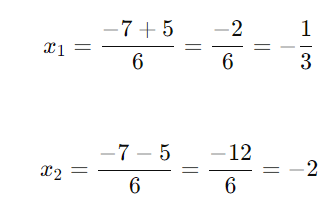
Resposta: As soluções são x1=−1/3 e x2=−2
Exercício 4
Enunciado: Resolva a equação 5x2 − 3x − 2 = 0.
Solução:
Para a equação 5x2 − 3x − 2 = 0, temos:
- a = 5
- b = -3
- c = -2
Calculando o discriminante Δ:
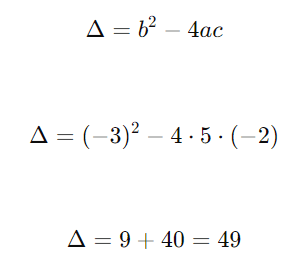
Substituindo na fórmula de Bhaskara:
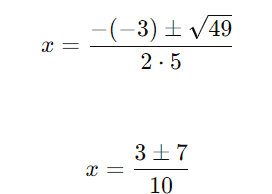
As raízes são:
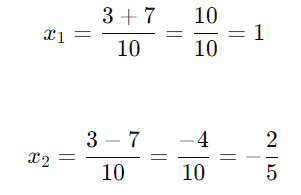
Resposta: As soluções são x1=1 e x2=−2/5
Exercício 5
Enunciado: Resolva a equação x2 + 2x − 8 = 0.
Solução:
Para a equação x2 + 2x − 8 = 0, temos:
- a = 1
- b = 2
- c = -8
Calculando o discriminante Δ:
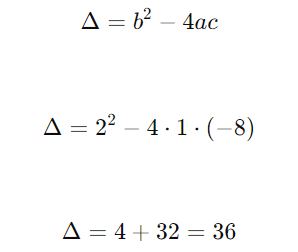
Substituindo na fórmula de Bhaskara:
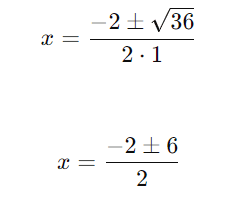
As raízes são:
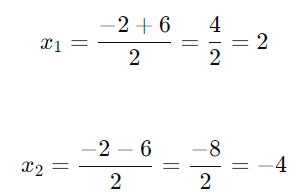
Resposta: As soluções são x1 = 2 e x2 = −4.
Aplicações das Equações do Segundo Grau
As equações do segundo grau aparecem em uma ampla variedade de contextos. Algumas das aplicações mais comuns incluem:
1. Física
Na física, as equações do segundo grau são frequentemente usadas para descrever o movimento de objetos. Por exemplo, a equação do movimento de um projétil é uma equação do segundo grau que descreve a trajetória parabólica do objeto.
2. Economia
Em economia, equações do segundo grau podem modelar várias situações, como o cálculo do lucro máximo de uma empresa. O ponto em que a receita e o custo se igualam pode ser determinado resolvendo uma equação do segundo grau.
3. Engenharia
Na engenharia, especialmente na análise de estruturas, as equações do segundo grau aparecem na determinação de tensões e deformações em materiais.
4. Geometria
Na geometria, as equações do segundo grau são usadas para encontrar interseções de círculos e outras cônicas, como elipses e hipérboles.
História e Curiosidades
A resolução de equações do segundo grau é uma das conquistas mais antigas da matemática. Os babilônios, por volta de 2000 a.C., já resolviam problemas que hoje reconheceríamos como equações do segundo grau. Eles usavam métodos geométricos e algébricos que se assemelham ao completamento de quadrado.
A fórmula que conhecemos hoje como “Fórmula de Bhaskara” foi desenvolvida por matemáticos indianos, como Bhaskara II, no século XII, embora variações dela fossem conhecidas na matemática grega e árabe. O nome é uma homenagem ao matemático indiano, mas a fórmula em si é um resultado do trabalho acumulado de várias culturas ao longo dos séculos.
Conclusão
As equações do segundo grau são um pilar da matemática, com aplicações que se estendem muito além da sala de aula. Desde resolver problemas do dia a dia até modelar fenômenos complexos na ciência e engenharia, essas equações desempenham um papel crucial em nossa compreensão do mundo.
Entender os diferentes métodos de resolução e a interpretação geométrica das equações do segundo grau não só melhora nossas habilidades matemáticas, mas também nos dá uma visão mais profunda de como a matemática pode ser aplicada na vida real.
Se você é estudante, professor ou entusiasta da matemática, continue explorando e













