Equação Exponencial: Um Guia Completo

Equações exponenciais aparecem frequentemente em problemas que envolvem crescimento, decaimento, juros compostos, e muitos outros fenômenos naturais e financeiros. Resolver equações exponenciais é essencial para entender e modelar essas situações. Neste artigo, exploraremos o que é uma equação exponencial, suas propriedades, métodos de resolução, e aplicações práticas.

Definição de Equação Exponencial

Uma equação exponencial é uma equação em que a variável desconhecida aparece no expoente. A forma geral de uma equação exponencial é:

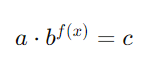
onde:

• a e c são constantes (a constante aaa geralmente é diferente de zero),
• b é a base da exponencial, que deve ser um número positivo diferente de 1,
• f(x) é uma função de x.

Exemplo:

2^x+1 = 8

Aqui, a base é 2 e a variável x aparece no expoente.

Propriedades das Equações Exponenciais

Algumas propriedades importantes das equações exponenciais incluem:

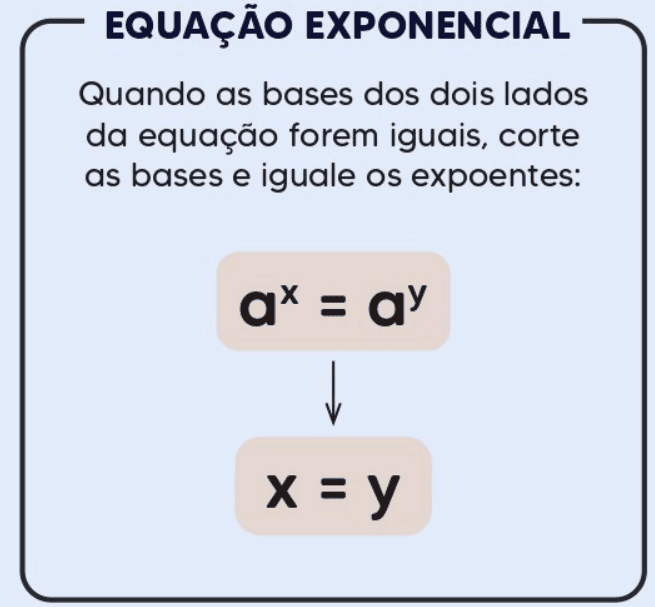
1. Mesma Base: Se duas expressões exponenciais têm a mesma base e são iguais, então seus expoentes também são iguais.
   Exemplo:
   Se 2^x+1=2³, então x+1=3.
2. Base Diferente: Quando as bases são diferentes, a equação pode ser resolvida aplicando logaritmos ou reescrevendo as bases em termos de um expoente comum.
3. Crescimento Rápido: Devido à natureza da função exponencial, pequenos aumentos no valor de xxx resultam em grandes mudanças no valor de b^f(x), especialmente quando a base b é maior que 1.

Métodos de Resolução de Equações Exponenciais

Resolver uma equação exponencial pode envolver vários métodos, dependendo da forma da equação. Vamos explorar alguns dos métodos mais comuns:

1. Comparação de Expoentes

Este método é utilizado quando as bases dos termos exponenciais são iguais.

Exemplo:
Resolva 3^2x=3⁵

Solução:
Como as bases são iguais, podemos igualar os expoentes:

2x = 5

x = 5/2

2. Reescrevendo as Bases

Se as bases não são iguais, mas podem ser reescritas como potências da mesma base, podemos igualar os expoentes.

Exemplo:
Resolva 4^x = 8

Solução:
Reescreva 4 e 8 como potências de 2:

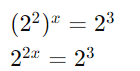
Agora, iguale os expoentes:

3. Uso de Logaritmos

Quando as bases não podem ser facilmente comparadas ou reescritas, usamos logaritmos para resolver a equação.

Exemplo:
Resolva

5^x = 20

Solução:
Aplique logaritmo em ambos os lados:

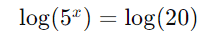
Use a propriedade do logaritmo:

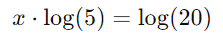
Resolva para x:

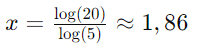
4. Isolamento da Exponencial

Em alguns casos, é útil isolar o termo exponencial antes de aplicar logaritmos ou outro método.

Exemplo:

Resolva

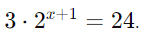
Solução:
Primeiro, isole o termo exponencial:

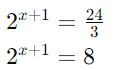
Reescreva 8 como uma potência de 2:

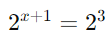
Iguale os expoentes:

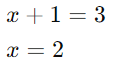
Aplicações Práticas das Equações Exponenciais

As equações exponenciais são usadas para modelar muitos fenômenos no mundo real:

1. Crescimento e Decaimento Populacional

Uma população que cresce a uma taxa constante pode ser modelada por uma equação exponencial (Função Exponencial). Se uma população inicial P₀​ cresce a uma taxa de r% por ano, após t anos, a população P(t) pode ser descrita por:

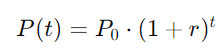
Exemplo:
Se uma cidade tem uma população inicial de 10.000 habitantes e cresce a uma taxa de 5% ao ano, determine a população após 3 anos.

Solução:

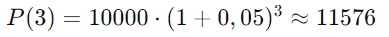
2. Decaimento Radioativo

O decaimento de substâncias radioativas é modelado por uma equação exponencial. A quantidade de material radioativo que permanece após um período t pode ser dada por:

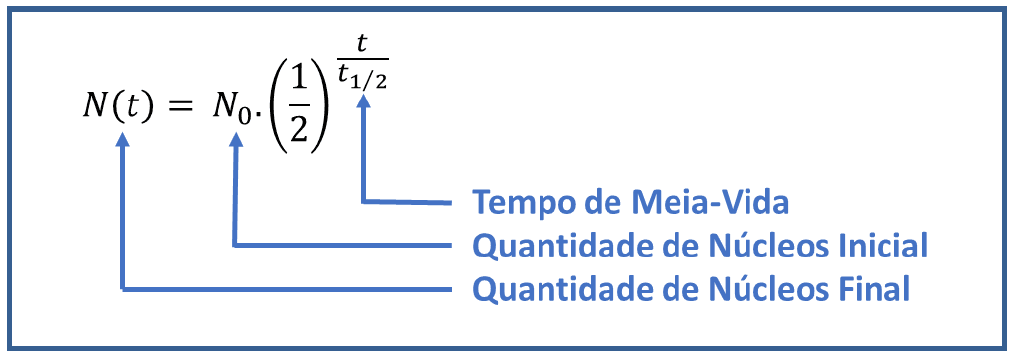
onde A₀​ é a quantidade inicial e t_1/2 é a meia-vida da substância.

Exemplo:
Se uma amostra de carbono-14 tem uma meia-vida de 5730 anos e inicialmente contém 50g, quantos gramas restarão após 10.000 anos?

Solução:

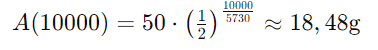
3. Juros Compostos

O valor de um investimento com juros compostos é determinado por uma equação exponencial:

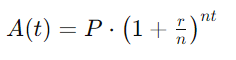
onde:

• P é o valor principal,
• r é a taxa de juros anual,
• n é o número de composições por ano,
• t é o tempo em anos.

Exemplo:
Se você investir R$ 1.000 a uma taxa de juros de 8% ao ano, compostos mensalmente, qual será o valor do investimento após 5 anos?

Solução:

Para resolver este problema, usaremos a fórmula do montante em juros compostos:

• A(t) é o valor futuro do investimento,
• P=1000 é o valor principal (investimento inicial),
• r=0,08 é a taxa de juros anual (8% ao ano),
• n=12 é o número de composições por ano (mensalmente),
• t=5 é o tempo em anos.

Substituindo os valores:

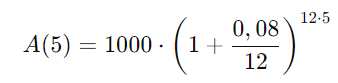
Primeiro, calcule o termo dentro dos parênteses:

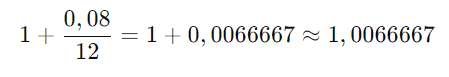
Agora, eleve este valor à potência 12 × 5=60:

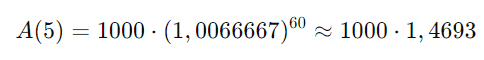
Finalmente, calcule o valor final:

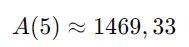
Portanto, o valor do investimento após 5 anos será aproximadamente R$ 1.469,33.

Exemplos de Resolução

Exemplo 1: Resolva 7^2x=343

Solução:
Escreva 343 como uma potência de 7

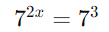
guale os expoentes:

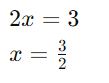
Exemplo 2: Resolva

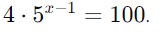
Solução:
Isole a exponencial:

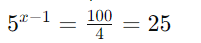
Reescreva 25 como uma potência de 5:

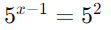
Iguale os expoentes:

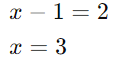
Conclusão

As equações exponenciais são fundamentais para modelar e resolver problemas que envolvem crescimento, decaimento, e outras mudanças rápidas no valor. Compreender os diferentes métodos de resolução e suas aplicações práticas é crucial para explorar o potencial dessas equações em diversas disciplinas, desde a matemática pura até as ciências aplicadas. Este guia oferece uma base sólida para trabalhar com equações exponenciais, seja em contextos acadêmicos ou práticos.