Aprenda Estatística na prática com esta seleção de 11 questões resolvidas passo a passo, incluindo gráficos de colunas, setores, histogramas, box-plots, tabelas de frequência e diagramas de ramos e folhas. Ideal para quem está estudando para o Ensino Médio, ENEM, concursos públicos e vestibulares. Os exercícios abordam média, moda, mediana, desvio padrão, porcentagem e interpretação de gráficos. Conteúdo completo, didático e com explicações claras para você dominar a estatística de forma definitiva.
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Interpretação de gráficos e cálculo de arrecadação
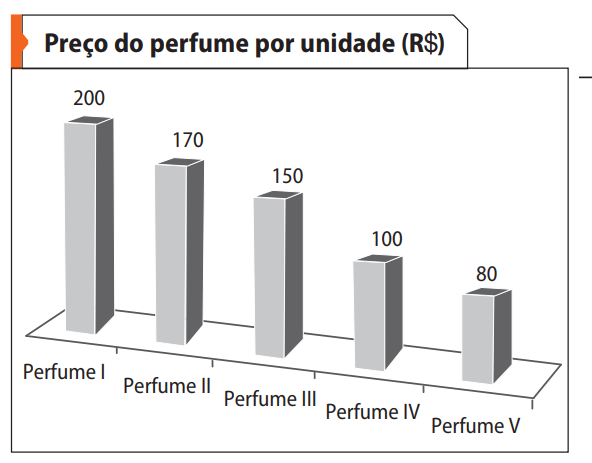
Questão 1. (Enem/MEC) O gerente de uma loja de cosméticos colocou à venda cinco diferentes tipos de perfume, tendo em estoque na loja as mesmas quantidades de cada um deles. O setor de controle de estoque encaminhou ao gerente registros gráficos descrevendo os preços unitários de cada perfume, em real, e a quantidade vendida de cada um deles, em percentual, ocorrida no mês de novembro.
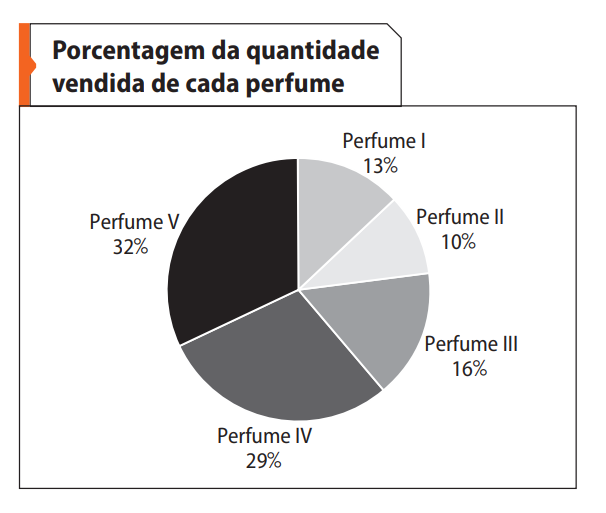
 Dados a chegada do final de ano e o aumento das vendas, a gerência pretende aumentar a quantidade estocada do perfume do tipo que gerou a maior arrecadação em espécie, em real, no mês de novembro. Nessas condições, qual o tipo de perfume que deverá ter maior reposição no estoque?
Dados a chegada do final de ano e o aumento das vendas, a gerência pretende aumentar a quantidade estocada do perfume do tipo que gerou a maior arrecadação em espécie, em real, no mês de novembro. Nessas condições, qual o tipo de perfume que deverá ter maior reposição no estoque?Alternativas:
a) I b) II c) III d) IV e) V
Ver Solução
Entendendo o enunciado:
Queremos saber qual perfume gerou a maior arrecadação total (preço × porcentagem vendida), já que todos tinham a mesma quantidade em estoque.
Cálculo da arrecadação proporcional (preço × percentual vendido):
- Perfume I: R$ 200 × 13 = R$ 2.600
- Perfume II: R$ 170 × 10 = R$ 1.700
- Perfume III: R$ 150 × 16 = R$ 2.400
- Perfume IV: R$ 100 × 29 = R$ 2.900
- Perfume V: R$ 80 × 32 = R$ 2.560
Conclusão:
O perfume que mais arrecadou em valor total foi o Perfume IV, com R$ 2.900. Portanto, é ele que deverá ter maior reposição no estoque.
Alternativa correta: d) IV
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Interpretação de gráficos e análise de dados oficiais
Questão 2. (Fuvest-SP) O Atlas da Violência, publicado em 2019 e organizado pelo Instituto de Pesquisa Econômica Aplicada e Fórum Brasileiro de Segurança Pública, apresenta um estudo para melhor compreender a violência no país. Os dados que ali constam referem-se ao período de 2007 a 2017. Um dos capítulos desse documento trata, especificamente, da violência contra a mulher. O gráfico a seguir mostra a evolução da taxa de homicídios de mulheres (número de homicídios por 100 mil mulheres), de 2007 a 2017, no Brasil e nas três unidades federativas com as menores taxas em 2017.
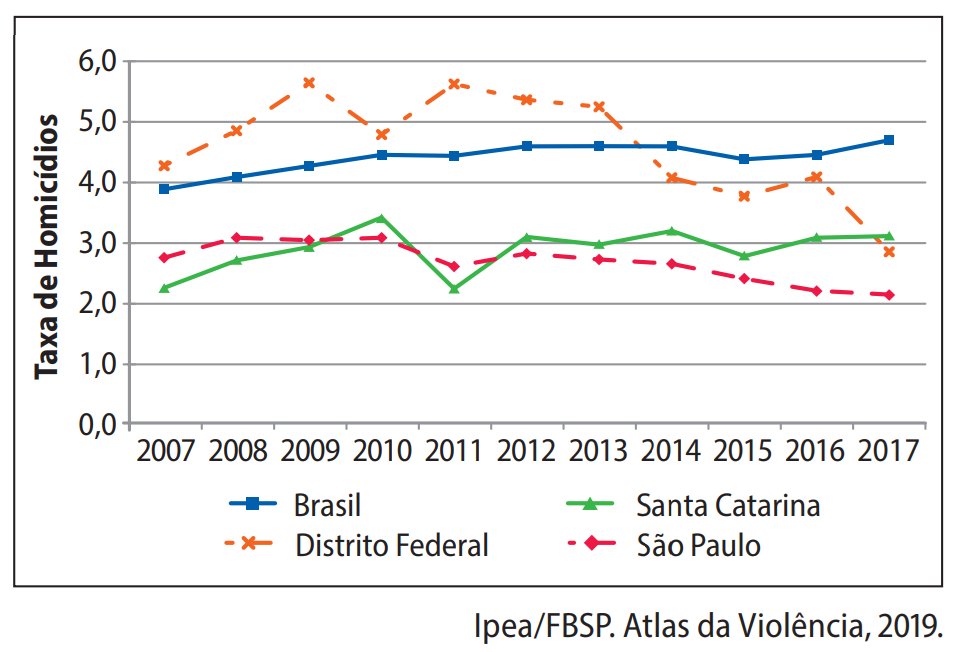 De acordo com os dados apresentados, é correto afirmar:
De acordo com os dados apresentados, é correto afirmar:Alternativas:
- a) Dentre as unidades federativas citadas, a que teve maior decréscimo na taxa de homicídios de mulheres no período entre 2014 e 2017 foi São Paulo.
- b) As três unidades federativas indicadas tiveram um decréscimo na taxa de homicídios de mulheres em 2017 quando comparada com a taxa de 2007.
- c) A taxa de homicídios de mulheres no Brasil em 2017 é maior do que a soma das taxas das três unidades federativas apresentadas neste mesmo ano.
- d) Dentre as unidades federativas apontadas, a que apresentou a maior taxa de homicídios de mulheres em 2017 é Santa Catarina, superando a taxa registrada nos estados da região Sul.
- e) Dentre as unidades federativas mencionadas, a maior redução na taxa de homicídios de mulheres, entre 2016 e 2017, registrada na pesquisa ocorreu no Distrito Federal.
Ver Solução
Entendendo o enunciado:
A questão pede que se avalie o comportamento da taxa de homicídios de mulheres entre os anos de 2016 e 2017, nas três unidades federativas com menores taxas em 2017: Distrito Federal, São Paulo e Santa Catarina.
Análise do gráfico:
- Distrito Federal: a linha vermelha tracejada mostra uma queda acentuada entre 2016 e 2017.
- Santa Catarina: linha verde com ligeira queda.
- São Paulo: linha rosa, queda muito pequena ou quase estável.
Conclusão:
O Distrito Federal foi a unidade com a maior redução registrada nesse período específico (2016–2017), conforme aponta claramente a linha do gráfico.
Alternativa correta: e) Dentre as unidades federativas mencionadas, a maior redução na taxa de homicídios de mulheres, entre 2016 e 2017, registrada na pesquisa ocorreu no Distrito Federal.
🧠 Mapas Mentais de MatemáticaConteúdo: Porcentagem e ângulos em gráficos de setores (gráficos de pizza)
Questão 3. (Saresp-SP) Uma escola tem alunos nos turnos da manhã (40%), da tarde (20%) e da noite (30%) e, ainda, alunos no turno único de tempo integral (10%). O gráfico de “pizza” mostra essas porcentagens, ilustradas por setores circulares com ângulos proporcionais às porcentagens.
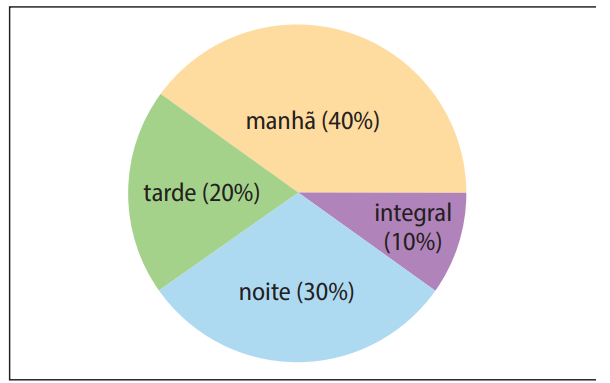 O ângulo, em graus, do setor de círculo correspondente ao turno da manhã é:
O ângulo, em graus, do setor de círculo correspondente ao turno da manhã é:Alternativas:
- a) 144°
- b) 108°
- c) 90°
- d) 120°
- e) 72°
Ver Solução
Entendendo o enunciado:
A questão quer saber qual é o ângulo correspondente ao setor do gráfico que representa 40% dos alunos.
Regra de três proporcional:
Como a circunferência total de um gráfico de pizza é de 360°, devemos calcular:
\[ \frac{40}{100} \times 360 = 0{,}4 \times 360 = \boxed{144^\circ} \]
Conclusão:
O setor correspondente aos alunos do turno da manhã mede 144 graus.
Alternativa correta: a) 144°
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Cálculo da mediana em dados agrupados por frequência
Questão 4. (UFRGS-RS) Após a aplicação de uma prova de Matemática, em uma turma de Ensino Médio com 30 estudantes, o professor organizou os resultados, conforme a tabela a seguir.
| Número de estudantes | Nota |
|---|---|
| 5 | 3,0 |
| 10 | 6,0 |
| 7 | 8,0 |
| 8 | 9,5 |
A nota mediana dessa prova de Matemática é:
Alternativas:
- a) 6,0
- b) 7,0
- c) 8,0
- d) 9,0
- e) 9,5
Ver Solução
Entendendo o enunciado:
Precisamos determinar a mediana, ou seja, a nota central da distribuição ordenada de 30 alunos. Como o número total de dados é par (30), a mediana será a média entre a 15ª e a 16ª nota.
Distribuindo os dados acumuladamente:
- Notas 3,0: 5 alunos → posições 1 a 5
- Notas 6,0: 10 alunos → posições 6 a 15
- Notas 8,0: 7 alunos → posições 16 a 22
- Notas 9,5: 8 alunos → posições 23 a 30
Verificando a posição da mediana:
– A 15ª nota está no grupo com nota 6,0
– A 16ª nota está no grupo com nota 8,0
Mediana = média entre 6,0 e 8,0:
\[ \frac{6{,}0 + 8{,}0}{2} = \frac{14}{2} = \boxed{7{,}0} \]
Conclusão:
A nota mediana é 7,0
Alternativa correta: b) 7,0
🧠 Mapas Mentais de MatemáticaConteúdo: Média aritmética – Problemas com repetição de valores
Questão 5. (UEA-AM) A média aritmética das notas das cinco melhores provas de matemática de uma turma é 8,0. Sabendo que somente duas dessas notas são iguais e que a média aritmética das outras três notas é 7,0, a nota que aparece repetida é:
Alternativas:
- a) 8,0
- b) 9,5
- c) 7,5
- d) 9,0
- e) 8,5
Ver Solução
Entendendo o enunciado:
A média das 5 notas é 8,0. Duas dessas notas são iguais e as outras três têm média 7,0. Devemos encontrar o valor da nota repetida.
Passo 1: Calcular o total das 5 notas:
\[ \text{Média} = \frac{\text{Soma total}}{5} \Rightarrow 8,0 = \frac{S}{5} \Rightarrow S = 40 \]
Passo 2: Calcular a soma das 3 notas diferentes:
\[ \text{Média} = \frac{S_3}{3} = 7,0 \Rightarrow S_3 = 21 \]
Passo 3: A soma das duas notas iguais será:
\[ 40 – 21 = 19 \]
Passo 4: Como as duas notas são iguais:
\[ 2x = 19 \Rightarrow x = \boxed{9{,}5} \]
Conclusão:
A nota que aparece repetida é 9,5.
Alternativa correta: b) 9,5
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Interpretação de gráfico de barras e média aritmética
Questão 6. (UERJ) O gráfico a seguir apresenta o quantitativo de mortes violentas de pessoas da comunidade LGBTQIA+, no ano de 2021, no Brasil.
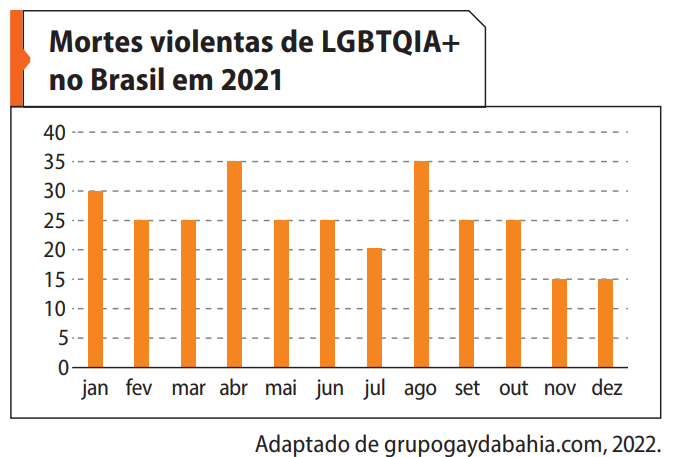 Com base nos dados do gráfico, calcule a média aritmética mensal de mortes violentas nessa comunidade, em 2021, no Brasil.
Com base nos dados do gráfico, calcule a média aritmética mensal de mortes violentas nessa comunidade, em 2021, no Brasil.Ver Solução
Entendendo o enunciado:
A média aritmética mensal é obtida somando o número de mortes em todos os meses e dividindo por 12.
Valores observados no gráfico:
- Janeiro: 30
- Fevereiro: 25
- Março: 25
- Abril: 35
- Maio: 25
- Junho: 25
- Julho: 20
- Agosto: 35
- Setembro: 25
- Outubro: 25
- Novembro: 15
- Dezembro: 15
Somando os valores:
\[ 30 + 25 + 25 + 35 + 25 + 25 + 20 + 35 + 25 + 25 + 15 + 15 = 300 \]
Cálculo da média mensal:
\[ \frac{300}{12} = \boxed{25} \]
Conclusão:
A média mensal de mortes violentas na comunidade LGBTQIA+ no ano de 2021 foi 25 mortes.
Conteúdo: Estatística – Análise de gráficos de dispersão e comparação com média
Questão 7. (Enem/MEC) Um professor, para promover a aprendizagem dos estudantes em estatística, propôs uma atividade. O objetivo era verificar o percentual de estudantes com massa corporal abaixo da média e altura acima da média de um grupo de estudantes. Para isso, usando uma balança e uma fita métrica, avaliou uma amostra de dez estudantes, anotando as medidas observadas. O gráfico apresenta a massa corporal, em quilograma, e a altura, em metro, obtidas na atividade.
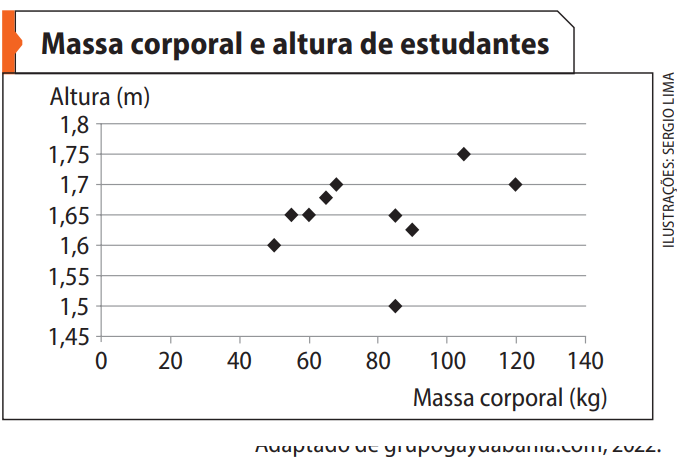 Após a coleta dos dados, os estudantes calcularam a média dos valores obtidos, referentes à massa corporal e à altura, obtendo, respectivamente, 80 kg e 1,65 m. Qual é o percentual de estudantes dessa amostra com massa corporal abaixo da média e altura acima da média?
Após a coleta dos dados, os estudantes calcularam a média dos valores obtidos, referentes à massa corporal e à altura, obtendo, respectivamente, 80 kg e 1,65 m. Qual é o percentual de estudantes dessa amostra com massa corporal abaixo da média e altura acima da média?Alternativas:
- a) 10
- b) 20
- c) 30
- d) 50
- e) 70
Ver Solução
Entendendo o enunciado:
Precisamos contar quantos pontos (estudantes) têm:
- Massa corporal abaixo de 80 kg
- Altura acima de 1,65 m
Análise do gráfico:
Há 10 pontos no gráfico. Vamos identificar quais estão na região abaixo de 80 kg e acima de 1,65 m.
Visualmente, observamos que apenas 2 pontos se enquadram nessa condição. Assim:
\[ \frac{2}{10} \times 100 = \boxed{20\%} \]
Conclusão:
O percentual de estudantes com massa corporal abaixo da média e altura acima da média é 20%.
Alternativa correta: b) 20
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Interpretação de histogramas, cálculo de média, mediana, porcentagem e frequência absoluta
Questão 8. (Unifesp-SP) Uma prova de estatística, valendo de 0 a 10 pontos, foi realizada por 253 alunos, sendo que nenhum tirou nota menor ou igual a 6. O histograma da figura 1 indica a distribuição das notas. Ainda que o eixo com a frequência de alunos em cada faixa de notas tenha sido omitido, foi fornecida a área de cada barra do histograma. A figura 2 ilustra o cálculo da mediana das notas.
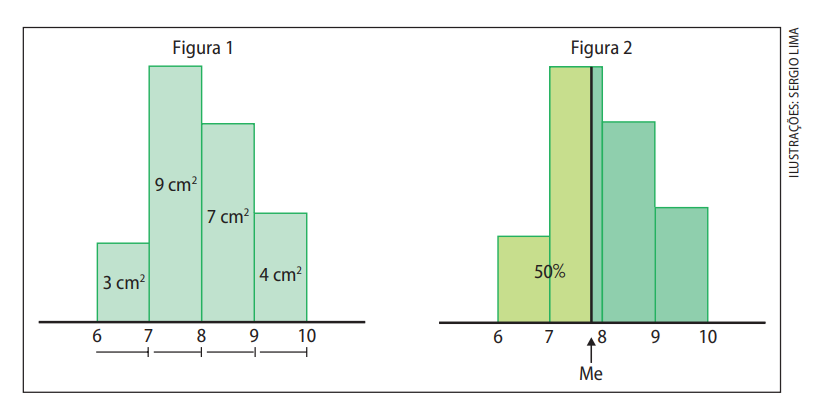
a) Calcule a porcentagem aproximada de alunos que tiraram nota menor ou igual a 7. Calcule a quantidade de alunos que tiraram nota maior que 8.
b) Calcule a média (M) e a mediana (Me) das notas usando aproximação de duas casas decimais, quando necessário.
Ver Solução
Entendendo o enunciado:
As áreas das barras representam proporcionalmente as quantidades de alunos por faixa. Vamos considerar que a soma total das áreas representa os 253 alunos.
Áreas das barras:
- 6–7: 3 cm²
- 7–8: 9 cm²
- 8–9: 7 cm²
- 9–10: 4 cm²
Total da área: \(3 + 9 + 7 + 4 = 23\)
Razão de conversão:
Cada cm² representa: \( \frac{253}{23} \approx 11\) alunos
a) Alunos com nota ≤ 7:
Faixa de 6–7: 3 cm² → \(3 × 11 = 33\) alunos
Porcentagem: \(\frac{33}{253} × 100 \approx 13\%\)
Alunos com nota > 8:
Faixas 9–10: 4 cm² → \(4 × 11 = 44\) alunos
\(\Rightarrow\) 121 alunos (soma de 7 cm² + 4 cm² = 11 cm² = \(11 × 11\))
b) Média (M) e Mediana (Me):
– Como estamos lidando com faixas, podemos usar os pontos centrais para estimar a média:
- 6,5 × 33 = 214,5
- 7,5 × 99 = 742,5
- 8,5 × 77 = 654,5
- 9,5 × 44 = 418
\[ \frac{214{,}5 + 742{,}5 + 654{,}5 + 418}{253} \approx \frac{2029{,}5}{253} \approx 8{,}02 \]
Mediana:
– O gráfico da Figura 2 mostra claramente que a mediana está na faixa 7–8, aproximadamente em 7,94.
Conclusão:
- Porcentagem com nota ≤ 7: 13%
- Alunos com nota > 8: 121 alunos
- Média \(M ≈ \mathbf{8{,}02}\)
- Mediana \(Me ≈ \mathbf{7{,}94}\)
Conteúdo: Estatística – Desvio padrão, interpretação de tabela e medidas de dispersão
Questão 9. (Enem/MEC) O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio.
Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão na tabela:
Tabela da questão:
| Atleta | 1ª pesagem (kg) | 2ª pesagem (kg) | 3ª pesagem (kg) | Média | Mediana | Desvio padrão |
|---|---|---|---|---|---|---|
| I | 78 | 72 | 66 | 72 | 72 | 4,90 |
| II | 83 | 65 | 65 | 71 | 65 | 8,49 |
| III | 75 | 70 | 65 | 70 | 70 | 4,08 |
| IV | 80 | 77 | 62 | 73 | 77 | 7,87 |
Texto:
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.
Pergunta:
A primeira luta foi entre os atletas:
Alternativas:
- a) I e III
- b) I e IV
- c) III e II
- d) II e IV
- e) III e IV
Ver Solução
Entendendo o enunciado:
A questão quer que identifiquemos:
- O atleta mais regular → menor desvio padrão
- O atleta menos regular → maior desvio padrão
Verificando os desvios padrão:
- I: 4,90
- II: 8,49
- III: 4,08 ← mais regular
- IV: 7,87
Mais regular: Atleta III
Menos regular: Atleta II
Conclusão:
A primeira luta será entre os atletas III e II.
Alternativa correta: c) III e II
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Diagrama de ramos e folhas, moda, mediana e organização de dados
Questão 10. (FCC) O diagrama de ramos e folhas a seguir corresponde às idades dos 40 funcionários de um setor de um órgão público em uma determinada data.
 A soma da mediana e da moda destas idades é igual a:
A soma da mediana e da moda destas idades é igual a:Alternativas:
- a) 67,0
- b) 66,5
- c) 66,0
- d) 65,5
- e) 65,0
Ver Solução
Entendendo o enunciado:
Devemos calcular a mediana e a moda das idades representadas no diagrama. O total de dados é 40.
Etapa 1 – Reescrevendo os dados do diagrama:
18, 18, 19,
20, 21, 21, 22, 22, 27, 28, 28, 29,
31, 33, 33, 33, 34, 34, 34, 35, 36, 37, 38, 38, 38,
40, 41, 42, 43, 44, 48, 49,
51, 55, 58,
62, 65
Etapa 2 – Moda:
O número mais frequente é 33 (aparece 3 vezes).
Etapa 3 – Mediana:
Temos 40 dados → mediana é a média entre o 20º e o 21º valores.
Percorrendo a lista em ordem crescente, temos:
20º valor = 34, 21º valor = 36
\[ \text{Mediana} = \frac{34 + 36}{2} = 35 \]
Etapa 4 – Soma:
\[
\text{Moda} + \text{Mediana} = 33 + 34 = \boxed{67,0}
\]
Conclusão:
A soma da moda e da mediana é 67,0.
Alternativa correta: a) 67,0
🧠 Mapas Mentais de MatemáticaConteúdo: Estatística – Interpretação de Boxplot (diagrama de caixa), mediana e quartis
Questão 11. (Ciaar) Observe o diagrama de caixa (box-plot) do peso de 50 pacientes antes e após a realização de um tratamento.
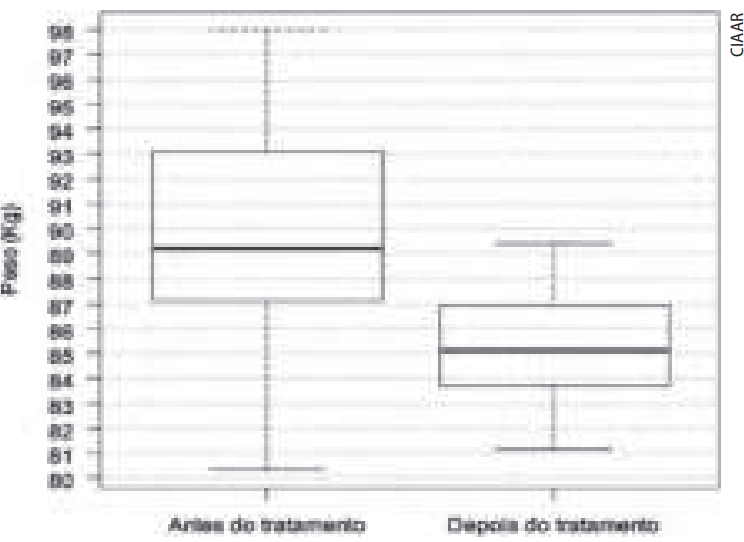 Com base nas informações do gráfico, analise as afirmativas abaixo:
Com base nas informações do gráfico, analise as afirmativas abaixo:- I. Antes do tratamento, o peso mediano dos pacientes era superior a 87 kg.
- II. Antes do tratamento, no mínimo, 25% dos pacientes pesavam 93 kg ou mais.
- III. Após o tratamento, 75% ou mais dos pacientes passaram a pesar menos de 84 kg.
- IV. Após o tratamento, 25% ou menos dos pacientes passaram a pesar de 83 kg a 87 kg.
Alternativas:
- a) III.
- b) I e II.
- c) II e IV.
- d) I, III e IV.
Ver Solução
Entendendo o boxplot:
No boxplot, temos:
- Mediana: linha dentro da caixa
- Q1 (1º quartil): 25% dos dados estão abaixo
- Q3 (3º quartil): 75% dos dados estão abaixo
Análise das afirmativas:
I – Verdadeira: A mediana “antes do tratamento” está acima da marca dos 87 kg.
II – Verdadeira: O Q3 (3º quartil) “antes do tratamento” é 93 kg, ou seja, 25% dos pacientes estão acima de 93 kg.
III – Falsa: Após o tratamento, o Q3 é 84 kg. Isso quer dizer que até 75% pesam **menos que ou igual** a 84 kg, e não **menos que**. Afirmativa é exagerada no “ou mais”.
IV – Falsa: Após o tratamento, o intervalo de 83 a 87 kg abrange uma porção central da caixa, não apenas 25% ou menos.
Conclusão:
As únicas afirmativas corretas são I e II.
Alternativa correta: b) I e II
🧠 Mapas Mentais de Matemática