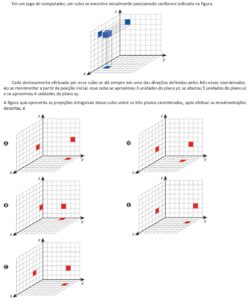
(CESPE / CEBRASPE 2024 – Prefeitura de Camaçari – BA – Professor Matemática)
Se a média aritmética de 23 números inteiros não negativos diferentes é 167, então, nessas condições, o maior valor que um desses números pode assumir é
A) 3.841.
B) 3.610.
C) 3.588.
D) 3.379.
E) 3.335.
Para resolver este problema, devemos usar o conceito de média aritmética e maximizar o valor de um dos números, sabendo que a média de 23 números inteiros diferentes não negativos é 167.
Passo a Passo:
- Calcular a soma total dos números:
A média aritmética de 23 números é dada por:
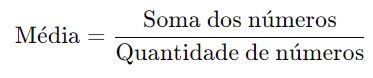
Substituindo os valores:
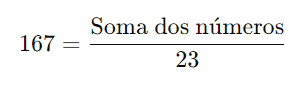
Multiplicando ambos os lados por 23:
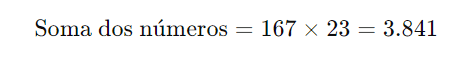
- Maximizar um dos números:
Para maximizar o valor de um dos números, vamos considerar que 22 números sejam os menores possíveis, que são 0, 1, 2, 3, …, 21. A soma desses 22 primeiros números é a soma dos 22 primeiros inteiros.
A soma dos primeiros (n) números inteiros é dada por:
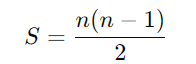
Para (n = 22):
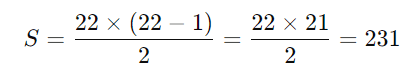
Agora, se a soma total é 3.841, e a soma dos 22 menores números é 231, o maior número possível (x) será:
x = 3.841 – 231 = 3.610
Conclusão:
O maior valor que um dos números pode assumir é 3.610.
Portanto, a resposta correta é:
B) 3.610.