Questão 26. Estude os sinais das funções definidas a seguir:
a) \( f(x) = x^2 – 3x – 10 \)
b) \( f(x) = -x^2 + 2x \)
c) \( f(x) = -4x^2 + 4x – 1 \)
d) \( f(x) = x^2 – x + 10 \)
a) 🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos determinar em quais intervalos a função é positiva ou negativa.
1) Raízes da equação:
$$ x^2 – 3x – 10 = 0 $$
Utilizando Bhaskara:
$$ \Delta = (-3)^2 – 4 \cdot 1 \cdot (-10) = 9 + 40 = 49 $$
$$ x = \frac{-(-3) \pm \sqrt{49}}{2 \cdot 1} = \frac{3 \pm 7}{2} $$
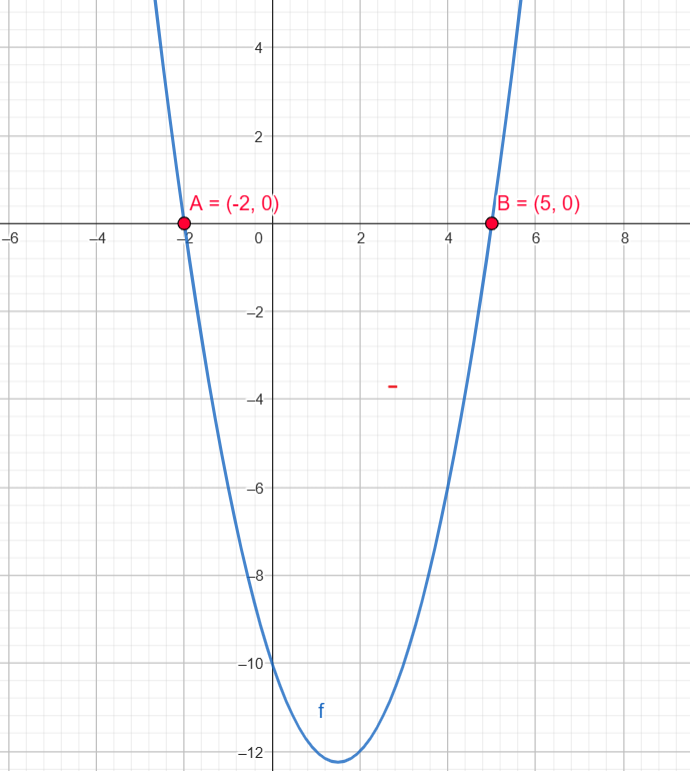
Raízes: \( x_1 = -2 \), \( x_2 = 5 \)
2) Estudo do sinal:
Como o coeficiente de \( x^2 \) é positivo, a parábola é voltada para cima:
- Negativa em \( (-2, 5) \)
- Positiva em \( (-\infty, -2) \cup (5, \infty) \)
- Nula em \( x = -2 \) e \( x = 5 \)
✅ Conclusão:
- f(x) > 0: \( x < -2 \) ou \( x > 5 \)
- f(x) = 0: \( x = -2 \) e \( x = 5 \)
- f(x) < 0: \( -2 < x < 5 \)
b) 🔍 Ver solução passo a passo
1) Raízes:
$$ -x^2 + 2x = 0 \Rightarrow x(-x + 2) = 0 $$
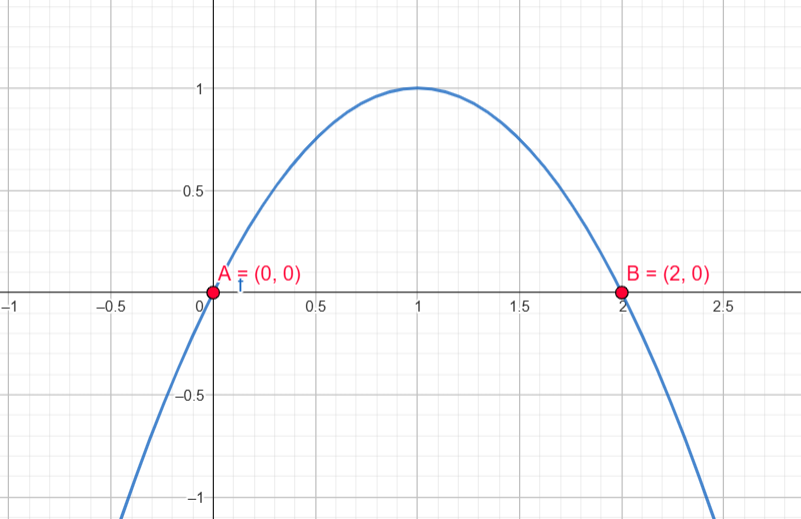
Raízes: \( x = 0 \) e \( x = 2 \)
2) Estudo do sinal:
Coeficiente de \( x^2 \) é negativo: concavidade para baixo
- Positiva entre \( (0, 2) \)
- Negativa fora desse intervalo
✅ Conclusão:
- f(x) > 0: \( 0 < x < 2 \)
- f(x) = 0: \( x = 0 \) e \( x = 2 \)
- f(x) < 0: \( x < 0 \) ou \( x > 2 \)
c) 🔍 Ver solução passo a passo
1) Raízes:
$$ f(x) = -4x^2 + 4x – 1 $$
$$ \Delta = 4^2 – 4 \cdot (-4) \cdot (-1) = 16 – 16 = 0 $$
Raiz dupla: \( x = \frac{-4}{2 \cdot -4} = \frac{1}{2} \)
2) Estudo do sinal:
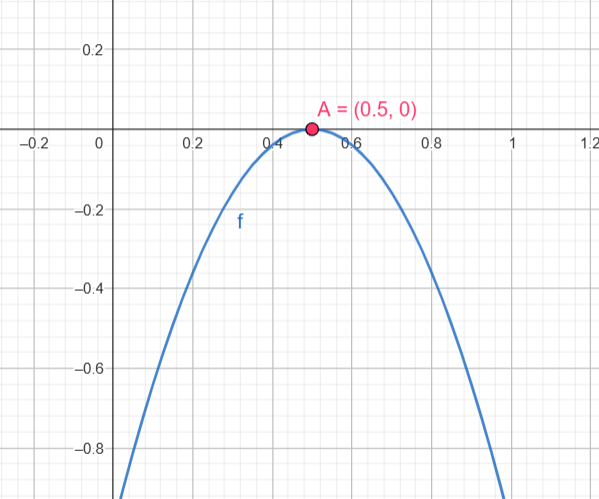
Parábola para baixo e toca o eixo em um único ponto:
- Nunca é positiva
- Apenas nula em \( x = \frac{1}{2} \)
- Negativa em todos os outros valores
✅ Conclusão:
- f(x) = 0: \( x = \frac{1}{2} \)
- f(x) < 0: \( x \neq \frac{1}{2} \)
d) 🔍 Ver solução passo a passo
1) Raízes:
$$ f(x) = x^2 – x + 10 $$
$$ \Delta = (-1)^2 – 4 \cdot 1 \cdot 10 = 1 – 40 = -39 $$
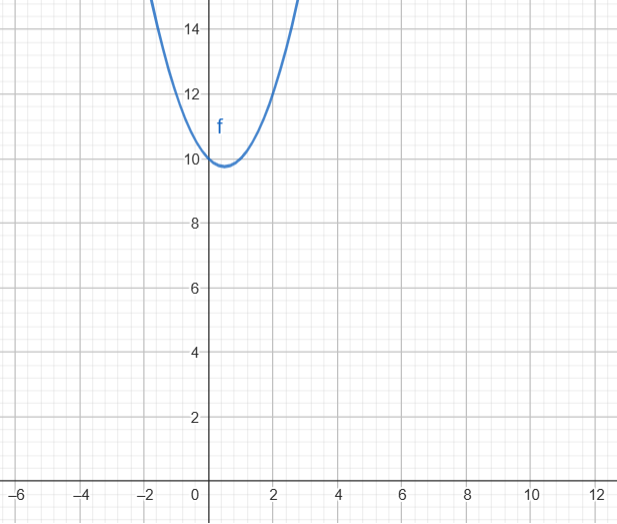
Não possui raízes reais.
2) Estudo do sinal:
Parábola para cima e não corta o eixo x. Portanto, é sempre positiva.
✅ Conclusão:
- f(x) > 0: Para todo \( x \in \mathbb{R} \)






















