Estudo do Sinal de Função Afim (1º grau)
Aprenda como descobrir quando \(f(x)=ax+b\) é positiva, nula ou negativa. Esse método resolve inequações lineares rapidamente e facilita a interpretação de gráficos. Para complementar, veja: Zero da função afim (x₀=−b/a) Construção do gráfico Taxa de variação (Δy/Δx) Função linear (b=0) Função constante (a=0)
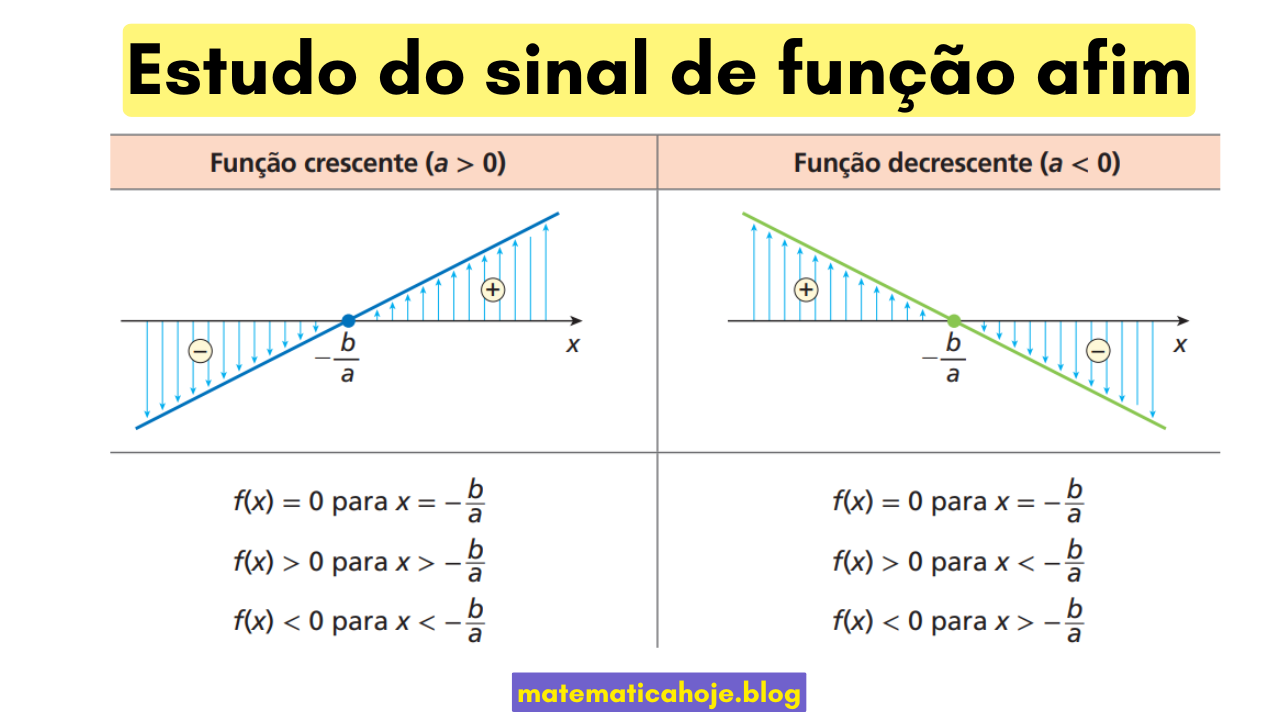
Regra prática com o zero \(x_0\)
Casos especiais (a=0): a função vira constante \(f(x)=b\). Se \(b>0\) é sempre positiva; se \(b<0\) é sempre negativa; se \(b=0\) é identicamente nula.
Tabela de sinal
| Situação | Zero \(x_0\) | f(x) < 0 | f(x) = 0 | f(x) > 0 |
|---|---|---|---|---|
| \(a>0\) (reta crescente) | \(-\dfrac{b}{a}\) | \(x\lt x_0\) | \(x=x_0\) | \(x\gt x_0\) |
| \(a<0\) (reta decrescente) | \(-\dfrac{b}{a}\) | \(x\gt x_0\) | \(x=x_0\) | \(x\lt x_0\) |
| \(a=0\) (constante) | — | \(b<0\) ⇒ todo \(x\) | \(b=0\) ⇒ todo \(x\) | \(b>0\) ⇒ todo \(x\) |
Passo a passo (inequações)
- Coloque na forma \(ax+b\ \square\ 0\) (\(\square\in\{<,\le,>,\ge\}\)).
- Calcule \(x_0=-\dfrac{b}{a}\) (se \(a\neq 0\)).
- Veja o sinal de \(a\) e escolha o(s) intervalo(s) corretos da tabela.
- Para \(\le\) ou \(\ge\), inclua \(x_0\) na resposta.
📘 Tenha a regra sempre à mão
Revise sinais, zeros e gráficos com o eBook Fórmulas Matemática — perfeito para ENEM e vestibulares.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Sinal completo de \(f(x)=3x-6\).
Ver solução
Zero: \(x_0=2\). Como \(a=3\gt 0\): \(f(x)\lt 0\) se \(x\lt 2\); \(f(x)=0\) em \(x=2\); \(f(x)\gt 0\) se \(x\gt 2\).
Exemplo 2 — Quando \(g(x)=-4x-8\) é positiva?
Ver solução
\(x_0=-2\). Como \(a=-4\lt 0\): \(g(x)\gt 0\) para \(x\lt -2\).
Exemplo 3 — Inequação linear. Resolva \( -2x+5 \ge 0\).
Ver solução
\(x_0=2{,}5\). Como \(a=-2\lt 0\): solução \(x\le 2{,}5\).
Exemplo 4 — Ponto de equilíbrio. O lucro é \(L(q)=1{,}8q-270\). Para quais \(q\) há prejuízo (\(L(q)\lt 0\))?
Ver solução
\(q_0=150\). Como \(a=1{,}8\gt 0\): prejuízo para \(q\lt 150\).
Erros comuns
- Trocar o sinal em \(-\dfrac{b}{a}\).
- Esquecer que o sinal de \(a\) inverte os intervalos.
- Confundir zero com intercepto em \(y\) (\(0,b\)).
Exercícios (gabarito no abre/fecha)
1) Estude o sinal de \(p(x)=5x-12\).
Ver gabarito
\(x_0=2{,}4\). \(a\gt 0\): \(p(x)\lt 0\) se \(x\lt 2{,}4\); \(=0\) em \(2{,}4\); >0 se \(x\gt 2{,}4\).
2) Resolva \(h(x)=-\dfrac{3}{2}x+6 > 0\).
Ver gabarito
\(x_0=4\). \(a\lt 0\): solução \(x\lt 4\).
3) Para \(f(x)=k\) (constante), classifique o sinal para \(k=7\), \(k=-2\) e \(k=0\).
Ver gabarito
7: sempre positiva; −2: sempre negativa; 0: nula para todo \(x\).
4) Determine \(x\) tais que \(3x+1 \le 0\).
Ver gabarito
\(x_0=-\dfrac{1}{3}\). \(a\gt 0\): solução \(x\le -\dfrac{1}{3}\).
5) Em qual intervalo \(r(x)=-0{,}8x-2\) é negativa?
Ver gabarito
\(x_0=-2{,}5\). \(a\lt 0\): negativa para \(x\gt -2{,}5\).
Continue estudando Função Afim
- Como construir o gráfico
- Zero de uma função afim
- Taxa de variação (Δy/Δx)
- Interseção de retas
- Função linear • Função constante













