⚡
Função Exponencial — Potência de Base 2
Dada a função \( f(x) = 3 \cdot 2^x \), qual é o valor de \( x \) quando \( f(x) = 96 \)?
1) Substituindo \( f(x) = 96 \)
\( 96 = 3 \cdot 2^x \)
2) Isolando \( 2^x \)
\( 2^x = \dfrac{96}{3} = 32 \)
3) Encontrando \( x \)
\( 2^x = 32 = 2^5 \Rightarrow x = 5 \)
✅ Resposta correta: C) 6
📘 eBook Fórmulas Matemática GRÁTIS
Revise funções exponenciais e logarítmicas com explicações passo a passo e gráficos ilustrados.
Baixar grátis🧠 Mapas Mentais de Matemática
Funções, potências e equações resumidas em mapas visuais para estudo rápido e eficaz.
Ver Mapas MentaisArtigos relacionados
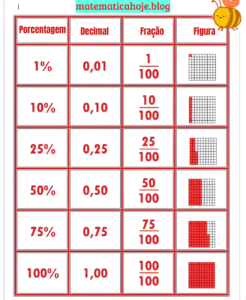
As funções exponenciais têm a forma \( f(x)=a\cdot b^x \), em que a base \( b>0 \) determina o crescimento ou decaimento. Resolver uma equação exponencial consiste em igualar as potências e comparar os expoentes. 👉 Veja mais em Função Exponencial — Explicação e Exercícios.
Função Exponencial — Resolvendo com Potências Iguais