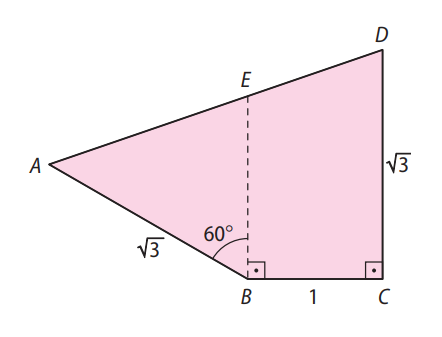
(Fuvest-SP) No quadrilátero \( ABCD \) da figura abaixo, \( E \) é um ponto sobre o lado \( AD \) tal que o ângulo \( \widehat{A \hat{B} E} \) mede \( 60^\circ \) e os ângulos \( \widehat{E \hat{B} C} \) e \( \widehat{B \hat{C} D} \) são retos. Sabe-se ainda que \( AB = CD = \sqrt{3} \, \text{m} \) e \( BC = 1 \, \text{m} \). Determine a medida de \( AD \).
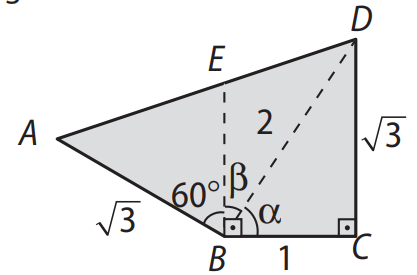
Utilizando o segmento auxiliar \( BD \), divide-se o quadrilátero nos triângulos \( DCB \) e \( ABD \).
1) Triângulo \( DCB \):
Como \( \sin \alpha = \frac{DC}{BD} = \frac{\sqrt{3}}{2} \), temos \( \alpha = 60^\circ \) e, portanto, \( \beta = 30^\circ \).
2) Triângulo \( ABD \):
Portanto, a medida de \( AD \) é \( \sqrt{7} \, \text{m} \).
📚 Indicação de Livros de Geometria
Volume 9: Geometria Plana
Aprenda todos os conceitos essenciais de geometria plana com exemplos práticos e detalhados.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Domine a geometria espacial com conteúdos claros e bem explicados para todos os níveis.
🔗 Acesse na Amazon
