Exercícios de Pirâmide Triangular – Situações-Problema (15 questões)
Pratique Geometria Espacial com contextos reais: embalagens, barracas, esculturas e estruturas. Abra as soluções quando precisar.
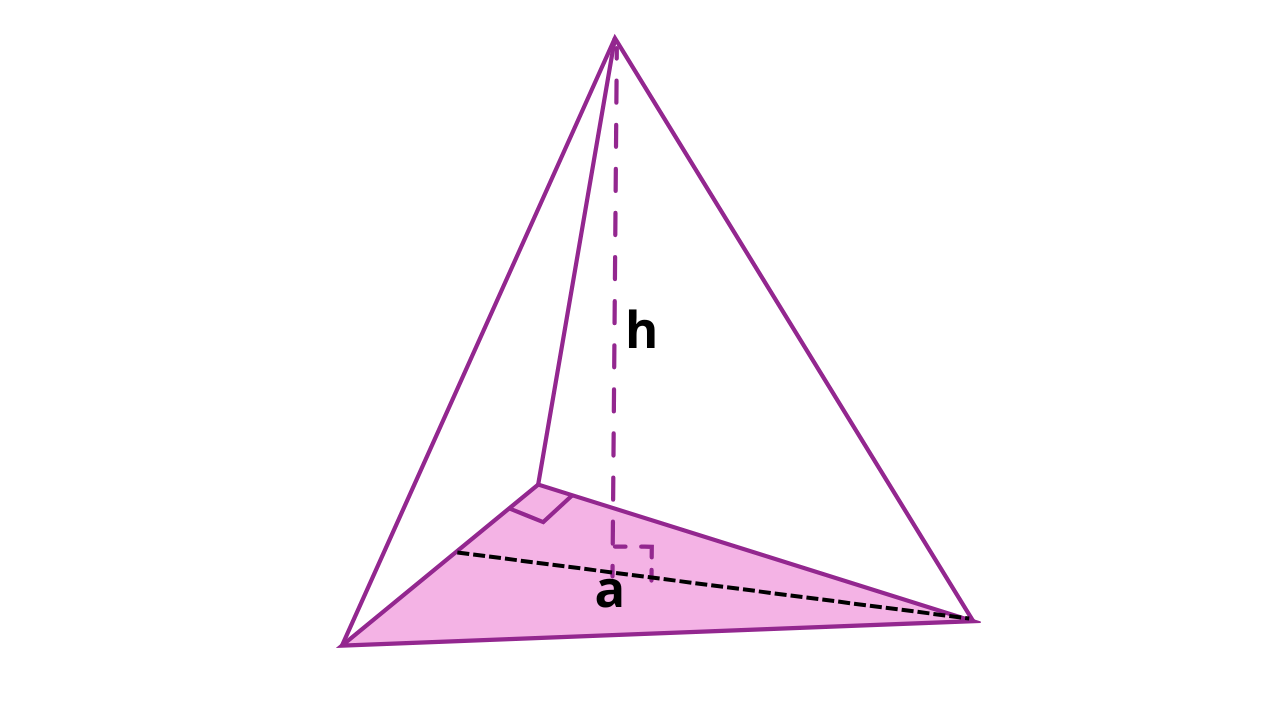
Fórmulas essenciais
Área da base (triângulo equilátero): \( A_b=\dfrac{a^2\sqrt{3}}{4} \)
Volume: \( V=\dfrac{1}{3}\,A_b\,h \)
Reveja a teoria em: Pirâmide, Exercício de Pirâmide, Pirâmide regular, Pirâmide quadrangular, Tronco de Pirâmide e Tronco de Pirâmide e Razões de Semelhança.
Lista de exercícios (múltipla escolha)
Questão 1 – Lembrancinha 3D
Um artesão corta uma base triangular equilátera de lado \(a=2\ \text{cm}\) para montar uma mini-pirâmide. Qual é a área dessa base?
- \(\sqrt{3}\ \text{cm}^2\)
- \(2\sqrt{3}\ \text{cm}^2\)
- \(3\sqrt{3}\ \text{cm}^2\)
- \(4\sqrt{3}\ \text{cm}^2\)
\(A_b=\frac{a^2\sqrt{3}}{4}=\frac{4\sqrt{3}}{4}=\mathbf{\sqrt{3}\ \text{cm}^2}\).
Gabarito: A
Questão 2 – Caixa decorativa
Uma caixinha em formato de pirâmide triangular tem base equilátera de lado \(a=4\ \text{cm}\). A área da base é:
- \(2\sqrt{3}\)
- \(3\sqrt{3}\)
- \(4\sqrt{3}\)
- \(16\sqrt{3}\)
\(A_b=\frac{16\sqrt{3}}{4}=\mathbf{4\sqrt{3}\ \text{cm}^2}\).
Gabarito: C
Questão 3 – Base de uma maquete
Para uma maquete de museu, será usada uma pirâmide triangular com base equilátera de \(a=6\ \text{cm}\). Qual é a área dessa base?
- \(6\sqrt{3}\)
- \(7\sqrt{3}\)
- \(8\sqrt{3}\)
- \(9\sqrt{3}\)
\(A_b=\frac{36\sqrt{3}}{4}=\mathbf{9\sqrt{3}\ \text{cm}^2}\).
Gabarito: D
Questão 4 – Mini tenda
Uma mini tenda de papel tem base equilátera de lado \(a=3\ \text{cm}\) e altura da pirâmide \(h=6\ \text{cm}\). Qual é o volume interno?
- \(4{,}5\sqrt{3}\ \text{cm}^3\)
- \(6\sqrt{3}\ \text{cm}^3\)
- \(9\sqrt{3}\ \text{cm}^3\)
- \(12\sqrt{3}\ \text{cm}^3\)
\(A_b=\frac{9\sqrt{3}}{4}\). \(V=\frac{1}{3}\cdot\frac{9\sqrt{3}}{4}\cdot6=\mathbf{4{,}5\sqrt{3}}\ \text{cm}^3\).
Gabarito: A
Questão 5 – Embalagem de perfume
Uma embalagem em forma de pirâmide triangular tem \(a=4\ \text{cm}\) e \(h=9\ \text{cm}\). Qual é o volume para comportar o líquido?
- \(8\sqrt{3}\)
- \(12\sqrt{3}\)
- \(16\sqrt{3}\)
- \(24\sqrt{3}\)
\(A_b=\frac{16\sqrt{3}}{4}=4\sqrt{3}\). \(V=\frac{1}{3}\cdot4\sqrt{3}\cdot9=\mathbf{12\sqrt{3}}\ \text{cm}^3\).
Gabarito: B
Questão 6 – Escultura de acrílico
Uma escultura tem formato de pirâmide triangular com \(a=10\ \text{cm}\) e \(h=15\ \text{cm}\). O volume de acrílico necessário é:
- \(50\sqrt{3}\)
- \(75\sqrt{3}\)
- \(100\sqrt{3}\)
- \(125\sqrt{3}\)
\(A_b=\frac{100\sqrt{3}}{4}=25\sqrt{3}\). \(V=\frac{1}{3}\cdot25\sqrt{3}\cdot15=\mathbf{125\sqrt{3}}\ \text{cm}^3\).
Gabarito: D
Questão 7 – Cobertura de vidro
Um topo de claraboia triangular usa base equilátera de \(a=12\ \text{cm}\). Para estimar os custos, a área da base é:
- \(18\sqrt{3}\)
- \(24\sqrt{3}\)
- \(30\sqrt{3}\)
- \(36\sqrt{3}\)
\(A_b=\frac{144\sqrt{3}}{4}=\mathbf{36\sqrt{3}\ \text{cm}^2}\).
Gabarito: D
Questão 8 – Barraca de camping (modelo)
Um protótipo de barraca tem base equilátera com \(a=8\ \text{cm}\) (em escala) e altura \(h=12\ \text{cm}\). O volume do protótipo é:
- \(32\sqrt{3}\)
- \(48\sqrt{3}\)
- \(64\sqrt{3}\)
- \(96\sqrt{3}\)
\(A_b=\frac{64\sqrt{3}}{4}=16\sqrt{3}\). \(V=\frac{1}{3}\cdot16\sqrt{3}\cdot12=\mathbf{64\sqrt{3}}\ \text{cm}^3\).
Gabarito: C
Questão 9 – Medalha em relevo
Uma medalha terá um relevo em forma de pirâmide triangular com base equilátera de lado \(a=5\ \text{cm}\). A área da base é:
- \(10\sqrt{3}\)
- \(\tfrac{25\sqrt{3}}{4}\)
- \(20\sqrt{3}\)
- \(12\sqrt{3}\)
\(A_b=\mathbf{\frac{25\sqrt{3}}{4}\ \text{cm}^2}\).
Gabarito: B
Questão 10 – Reservatório didático
Um reservatório de laboratório, em forma de pirâmide triangular, tem base de lado \(a=6\ \text{cm}\) e altura \(h=12\ \text{cm}\). Qual é a sua capacidade (volume)?
- \(24\sqrt{3}\)
- \(36\sqrt{3}\)
- \(54\sqrt{3}\)
- \(72\sqrt{3}\)
\(A_b=9\sqrt{3}\). \(V=\frac{1}{3}\cdot9\sqrt{3}\cdot12=\mathbf{36\sqrt{3}}\ \text{cm}^3\).
Gabarito: B
Questão 11 – Bloco de construção
Um bloco didático tem formato de pirâmide triangular com \(a=9\ \text{cm}\) e \(h=8\ \text{cm}\). Qual é o volume do bloco?
- \(54\sqrt{3}\)
- \(81\sqrt{3}\)
- \(108\sqrt{3}\)
- \(162\sqrt{3}\)
\(A_b=\frac{81\sqrt{3}}{4}\). \(V=\frac{1}{3}\cdot\frac{81\sqrt{3}}{4}\cdot8=\mathbf{54\sqrt{3}}\ \text{cm}^3\).
Gabarito: A
Questão 12 – Monumento urbano
Um pequeno monumento em formato de pirâmide triangular tem \(a=15\ \text{cm}\) (no modelo reduzido) e \(h=20\ \text{cm}\). Estime o volume do modelo.
- \(225\sqrt{3}\)
- \(300\sqrt{3}\)
- \(375\sqrt{3}\)
- \(450\sqrt{3}\)
\(A_b=\frac{225\sqrt{3}}{4}\). \(V=\frac{1}{3}\cdot\frac{225\sqrt{3}}{4}\cdot20=\mathbf{375\sqrt{3}}\ \text{cm}^3\).
Gabarito: C
Questão 13 – Cobertura de pavilhão (maquete)
Em uma maquete, a cobertura é uma pirâmide triangular com \(a=18\ \text{cm}\) e \(h=24\ \text{cm}\). Qual é o volume da cobertura?
- \(432\sqrt{3}\)
- \(486\sqrt{3}\)
- \(648\sqrt{3}\)
- \(576\sqrt{3}\)
\(A_b=\frac{324\sqrt{3}}{4}=81\sqrt{3}\). \(V=\frac{1}{3}\cdot81\sqrt{3}\cdot24=\mathbf{648\sqrt{3}}\ \text{cm}^3\).
Gabarito: C
Questão 14 – Pirâmide de vidro
Uma pirâmide de vidro deve ter área de base \(A_b=25\sqrt{3}\ \text{cm}^2\) e altura \(h=18\ \text{cm}\). Qual é o volume projetado?
- \(120\sqrt{3}\)
- \(130\sqrt{3}\)
- \(140\sqrt{3}\)
- \(150\sqrt{3}\)
\(V=\frac{1}{3}\cdot25\sqrt{3}\cdot18=25\cdot6\sqrt{3}=\mathbf{150\sqrt{3}}\ \text{cm}^3\).
Gabarito: D
Questão 15 – Protótipo de silo
Um protótipo de silo em forma de pirâmide triangular possui base equilátera com \(a=20\ \text{cm}\) e altura \(h=30\ \text{cm}\). Determine o volume.
- \(500\sqrt{3}\)
- \(1000\sqrt{3}\)
- \(1500\sqrt{3}\)
- \(2000\sqrt{3}\)
\(A_b=\frac{400\sqrt{3}}{4}=100\sqrt{3}\). \(V=\frac{1}{3}\cdot100\sqrt{3}\cdot30=\mathbf{1000\sqrt{3}}\ \text{cm}^3\).
Gabarito: B






















