A fatoração é uma das ferramentas mais poderosas da álgebra, essencial para simplificar expressões e resolver equações. Ela permite decompor uma expressão algébrica em fatores mais simples, facilitando operações matemáticas e resoluções de problemas. Vamos explorar as principais técnicas de fatoração, como evidência, agrupamento, diferença de dois quadrados, trinômio quadrado perfeito, soma de dois cubos e diferença de dois cubos.
1. Fatoração por Evidência
A fatoração por evidência, também conhecida como fatoração de termo comum, é a forma mais básica de fatoração. Consiste em identificar e extrair o fator comum dos termos de uma expressão.
Exemplo:
2x2 + 4x = 2x(x + 2)
Neste exemplo, o termo comum aos dois membros é 2x . Ao extraí-lo, ficamos com a expressão 2x(x + 2).

2. Fatoração por Agrupamento
A fatoração por agrupamento é útil quando lidamos com expressões que possuem quatro ou mais termos. O objetivo é agrupar os termos de forma que cada grupo tenha um fator comum, permitindo a aplicação da evidência.
Exemplo:
x3 + 3x2 + 2x + 6
Podemos agrupar os termos como:
(x3 + 3x2) + (2x + 6)
Agora, fatoramos cada grupo:
x2(x + 3) + 2(x + 3)
Finalmente, podemos extrair o fator comum (x + 3):
(x + 3)(x2 + 2)

3. Diferença de Dois Quadrados
A diferença de dois quadrados é um caso especial de fatoração que ocorre quando temos uma expressão da forma a2 – b2. Essa expressão pode ser fatorada como (a – b)(a + b).
Exemplo:
x2 – 16 = x2 – 42 = (x – 4)(x + 4)
Aqui, (x2) e (16) são quadrados perfeitos, permitindo a fatoração na forma (x – 4)(x + 4).

4. Trinômio Quadrado Perfeito
Um trinômio quadrado perfeito é uma expressão da forma a2 + 2ab + b2 ou a2 – 2ab + b2. Ele pode ser fatorado como (a + b)2 ou (a – b)2, respectivamente.
Exemplo:
x2 + 6x + 9 = (x + 3)2
Aqui, x2 é o quadrado de x, 6x é duas vezes x vezes 3, e 9 é o quadrado de 3, resultando em (x + 3)2.

5. Soma de Dois Cubos
A soma de dois cubos segue a fórmula:
a3 + b3 = (a + b)(a2 – ab + b2)
Exemplo:
x3 + 8 = (x + 2)(x2 – 2x + 4)
Aqui, x3 é x elevado ao cubo e 8 é 23.
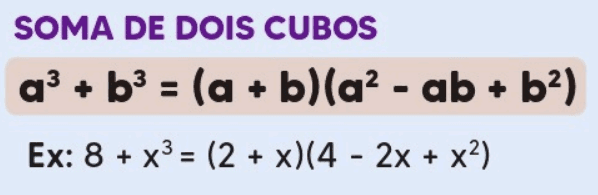
6. Diferença de Dois Cubos
A diferença de dois cubos pode ser fatorada usando a fórmula:
a3 – b3 = (a – b)(a2 + ab + b2)
Exemplo:
x3 – 27 = (x – 3)(x2 + 3x + 9)
Neste caso, x3 é x elevado ao cubo e 27 é 33.

Conclusão
Dominar as técnicas de fatoração é crucial para avançar em álgebra e resolver problemas matemáticos mais complexos. Cada método serve a um propósito específico, e com a prática, você pode determinar rapidamente qual técnica aplicar a cada expressão. Compreender e aplicar essas técnicas de forma fluida abre portas para explorar a matemática de maneira mais profunda e eficiente.