Matemática – FGV 2025 – Nível Médio
Conteúdo: Geometria Espacial — Volume de paralelepípedo
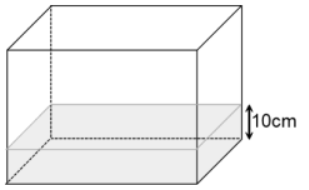
A figura mostra um pequeno tanque de vidro, com a forma de um paralelepípedo reto retângulo, cujas dimensões medem 60 cm × 40 cm × 40 cm.
O tanque está parcialmente cheio com água, e o nível d’água está a 10 cm do fundo do tanque.
Se esse tanque for virado e colocado na vertical, apoiado sobre sua face quadrada, então o nível d’água estará a uma distância do fundo do tanque que mede
O tanque está parcialmente cheio com água, e o nível d’água está a 10 cm do fundo do tanque.
Se esse tanque for virado e colocado na vertical, apoiado sobre sua face quadrada, então o nível d’água estará a uma distância do fundo do tanque que mede
A) 50 cm
B) 40 cm
C) 30 cm
D) 20 cm
E) 15 cm
Ver solução passo a passo
1) Volume de água inicialmente:
Base = 60 × 40
Altura da água = 10 cm
Volume = 60 × 40 × 10 = 24.000 cm³
2) Ao virar o tanque, ele fica apoiado sobre a face quadrada 40 × 40.
Nova base = 40 × 40 = 1.600 cm²
3) Seja h a nova altura da água:
1.600 × h = 24.000
h = 24.000 / 1.600
h = 15 cm
Resposta correta: alternativa E) 15 cm.





















