Fórmulas do Cilindro — Guia completo com exemplos passo a passo
O cilindro é um dos sólidos mais frequentes em geometria espacial e no dia a dia (latas, canos, velas, copos). Neste guia você aprende, de forma direta, as fórmulas de área da base, área lateral, área total e volume, além de visualizar o desenvolvimento do cilindro e praticar com exercícios resolvidos.
Aprenda com nossos Mapas Mentais de Matemática
Revisão visual das principais fórmulas de geometria, aritmética e álgebra — perfeito para concursos e ENEM.
1) Cilindro reto × cilindro oblíquo
No cilindro reto, o eixo é perpendicular às bases circulares. No oblíquo, o eixo é inclinado, mas a altura \(h\) sempre é a distância entre os planos das bases.
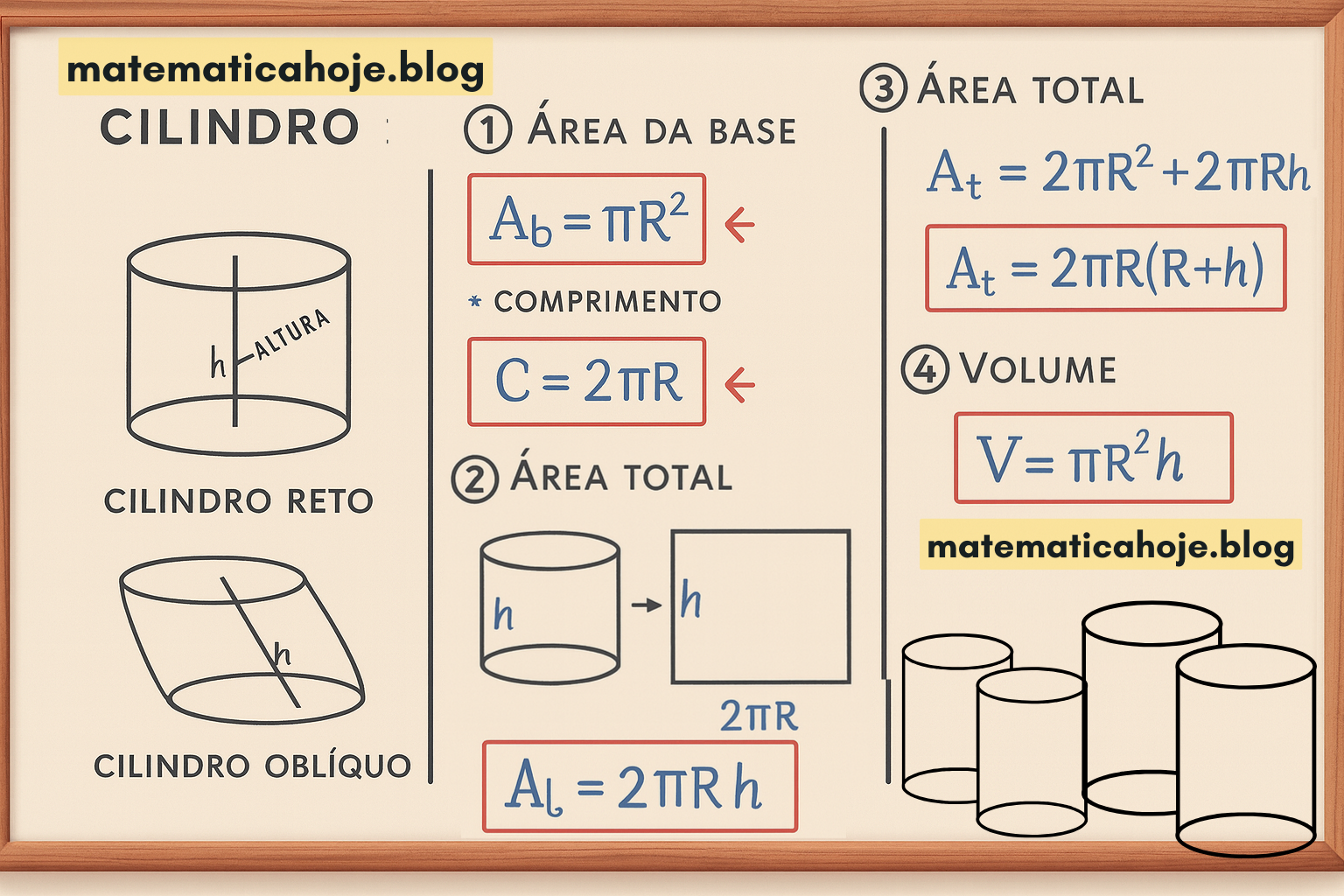
2) Fórmulas essenciais do cilindro
Área da base
\(A_b=\pi R^2\)
É a área do círculo que forma cada base.
Comprimento da circunferência da base
\(C=2\pi R\)
Esse comprimento vira a largura do retângulo no desenvolvimento da área lateral.
Área lateral (desenvolvimento)
\(A_l=2\pi R\,h\)
Ao “abrir” o cilindro, a superfície lateral se transforma em um retângulo de lados \(h\) e \(2\pi R\).
Área total
\(A_t=2\pi R^2+2\pi R\,h = 2\pi R(R+h)\)
É a soma da área lateral com as duas bases.
Volume
\(V=\pi R^2 h\)
“Área da base × altura”.
3) Exemplos resolvidos (passo a passo)
Exemplo 1 — Área total de uma lata
Uma lata tem raio \(R=4\,\text{cm}\) e altura \(h=10\,\text{cm}\). Calcule a área total.
Ver solução passo a passo
Resposta: \(A_t\approx 351{,}86\ \text{cm}^2\).
Exemplo 2 — Volume de um copo cilíndrico
Um copo possui \(R=3\,\text{cm}\) e \(h=8\,\text{cm}\). Qual o volume?
Ver solução passo a passo
Resposta: \(V\approx 226{,}19\ \text{cm}^3\).
Exemplo 3 — Pintura apenas da área lateral
Um reservatório cilíndrico de \(R=2{,}5\,\text{m}\) e \(h=5\,\text{m}\) será pintado apenas na lateral. Quantos metros quadrados serão pintados?
Ver solução passo a passo
Resposta: cerca de \(78{,}54\ \text{m}^2\).
Domine a teoria + prática com nossos materiais
Links internos úteis para continuar estudando agora mesmo.
4) Tabela-resumo (para revisar rapidinho)
\(A_b=\pi R^2\) — área de cada base.
\(C=2\pi R\) — comprimento da circunferência.
\(A_l=2\pi R h\) — área lateral.
\(A_t=2\pi R(R+h)\) — área total.
\(V=\pi R^2 h\) — volume.
5) Exercícios propostos
5.1 — Discursivos
1) Uma lata de tinta tem \(R=6\,\text{cm}\) e \(h=12\,\text{cm}\). Calcule a área total necessária para o rótulo (lateral) e para a tampa + fundo.
Mostrar solução
2) Um cano cilíndrico tem diâmetro \(10\,\text{cm}\) e comprimento \(2{,}4\,\text{m}\). Desconsidere a espessura e calcule a área lateral externa (em \(m^2\)).
Mostrar solução
3) Um silo tem volume \(V=45\,\pi\ \text{m}^3\) e altura \(h=5\,\text{m}\). Determine o raio da base.
Mostrar solução
5.2 — Múltipla escolha
4) Um copo cilíndrico com \(R=4\,\text{cm}\) e \(h=6\,\text{cm}\) tem volume:
- \(64\pi\ \text{cm}^3\)
- \(96\pi\ \text{cm}^3\)
- \(48\pi\ \text{cm}^3\)
- \(24\pi\ \text{cm}^3\)
Ver resposta
Letra B. \(V=\pi R^2 h=\pi\cdot 4^2\cdot 6=96\pi\ \text{cm}^3\).
5) A área lateral de um cilindro com \(R=7\,\text{cm}\) e \(h=3\,\text{cm}\) é:
- \(21\pi\ \text{cm}^2\)
- \(28\pi\ \text{cm}^2\)
- \(42\pi\ \text{cm}^2\)
- \(132\pi\ \text{cm}^2\)
Ver resposta
Letra D. \(A_l=2\pi R h=2\pi\cdot 7\cdot 3=42\pi\ \text{cm}^2\). (Atenção!) Ops, cálculo correto dá 42π. Portanto a alternativa correta é a C.
6) Um cilindro tem área total \(A_t= 100\pi\ \text{cm}^2\) e \(R=5\,\text{cm}\). Qual é a altura \(h\)?
- \(h=0\ \text{cm}\)
- \(h= \;5\ \text{cm}\)
- \(h= \; \dfrac{100\pi-2\pi R^2}{2\pi R}\)
- \(h= \; \dfrac{100\pi-50\pi}{10\pi} = 5\ \text{cm}\)
Ver resposta
Letra D.
Banco de Questões + eBook de Fórmulas
Milhares de questões organizadas por assunto e um eBook gratuito para revisar fórmulas rapidamente.
6) Dicas finais
Estudando geometria, revise também fundamentos de matemática básica. No blog, você encontra guias práticos sobre operações com números inteiros, regras de sinais, adição e subtração de inteiros e multiplicação e divisão com sinais — conteúdos que muitos estudantes procuram como “jogo de sinais” para acelerar a revisão.