A geometria plana é uma das bases fundamentais da matemática, sendo amplamente utilizada para resolver problemas do dia a dia e em contextos acadêmicos. As fórmulas geometria plana dentro das Fórmulas Matemática, são ferramentas indispensáveis para o cálculo de áreas, perímetros, ângulos e outras propriedades de figuras planas como triângulos, quadriláteros, círculos e polígonos regulares. Neste artigo, você vai encontrar um guia detalhado sobre as principais fórmulas de geometria plana, com exemplos práticos e explicações claras.
O Que É Geometria Plana?
A geometria plana é a área da matemática que estuda as figuras bidimensionais, ou seja, aquelas que possuem apenas comprimento e largura. Entre as figuras mais estudadas na geometria plana estão:
- Triângulos (equiláteros, isósceles e escaleno);
- Quadriláteros (quadrado, retângulo, losango e trapézio);
- Círculos;
- Polígonos regulares (pentágono, hexágono, etc.).
O foco principal da geometria plana é compreender e calcular propriedades como área, perímetro, diâmetros e ângulos internos das figuras.
Principais Fórmulas de Geometria Plana
1. Fórmulas para Triângulos

Área do Triângulo: A = b⋅h/2
Onde:
b: base do triângulo;
h: altura relativa à base.
Perímetro do Triângulo:
P = a + b + c
Onde a, b e c são os lados do triângulo.
Teorema de Pitágoras (triângulo retângulo):
a2 + b2 = c2
Onde c é a hipotenusa e a e b são os catetos.
Confira também as fórmula de Bhaskara
2. Fórmulas para Quadriláteros
Área do Quadrado:
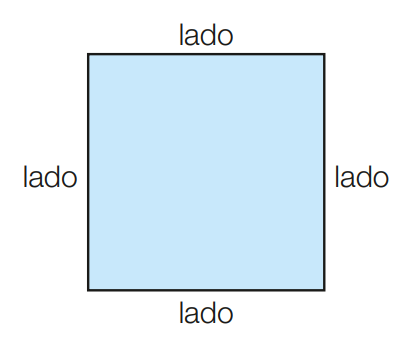
A = l2
Onde l é o lado do quadrado.
Perímetro do Quadrado:
P = 4l
Área do Retângulo:
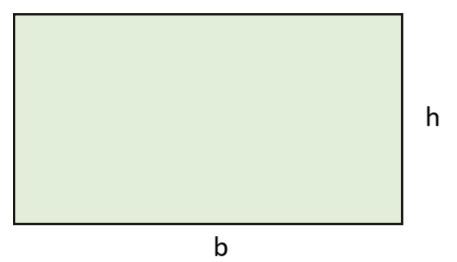
A = b⋅h
Onde:
b: base;
h: altura.
Perímetro do Retângulo:
P = 2b + 2h
Área do Losango:
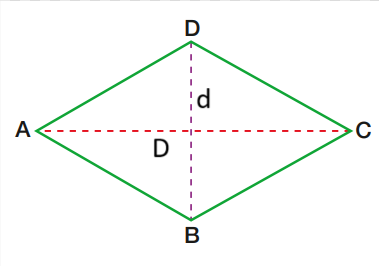
A = D⋅d/2
Onde:
D: diagonal maior;
d: diagonal menor.
Área do Trapézio:
A = [(B+b)⋅h]/2
Onde:
B: base maior;
b: base menor;
h: altura.
Confira também as análise combinatória
3. Fórmulas para Círculos
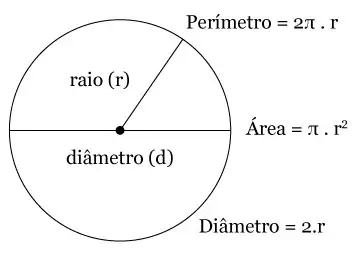
Área do Círculo:
A =π⋅r2
Onde r é o raio.
Comprimento da Circunferência:
C =2π⋅r
Setor Circular (área):
A = θ⋅π⋅r2/360
Onde θ é o ângulo central em graus.
4. Fórmulas para Polígonos Regulares
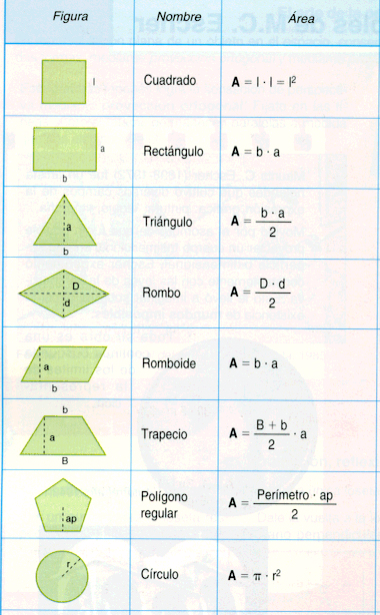
Área de um Polígono Regular:
A = n⋅l⋅a/2
Onde:
n: número de lados;
l: comprimento de cada lado;
a: apótema.
Soma dos Ângulos Internos:
S = (n − 2)⋅180°
Medida de Cada Ângulo Interno (Polígonos Regulares):
Ângulo Interno = (n − 2)⋅180
Propriedades Importantes em Geometria Plana
Diagonais de Polígonos: O número de diagonais em um polígono com n lados é dado por:
D = n⋅(n−3)/2
Razões Métricas:
Em triângulos retângulos, relações entre os lados são baseadas no Teorema de Pitágoras.
A altura em triângulos equiláteros é dada por:
h = √3/2⋅l
Comprimento de Arco:
L = θ⋅2πr/360
Diâmetro e Raio: O diâmetro é duas vezes o raio:
D = 2r
Confira também as fórmula de permutação
Exemplo Prático: Calculando Áreas e Perímetros
Problema: Qual é a área e o perímetro de um círculo com raio de 7 cm?
Cálculo da área:
A = π⋅r2 = 3,14⋅72 = 153,86 cm2
Cálculo do comprimento da circunferência:
C = 2π⋅r = 2⋅3,14⋅7 = 43,96 cm
Confira também as formulas geometria espacial
Dicas para Memorizar as Fórmulas de Geometria Plana
- Pratique Regularmente: Resolva exercícios que envolvam diferentes figuras.
- Crie Mapas Mentais: Organize as fórmulas em categorias para facilitar a memória.
- Relacione com o Cotidiano: Aplique as fórmulas em situações reais, como medir espaços e calcular materiais.
Entre para o nosso Canal do WhatsApp
Conclusão
Dominar as fórmulas de geometria plana é essencial para resolver problemas em diversos contextos, desde o dia a dia até situações acadêmicas e profissionais. Com este guia, você tem as ferramentas necessárias para calcular áreas, perímetros e outras propriedades das figuras planas com confiança e precisão. Continue praticando e explore o fascinante universo da geometria!






















