Confira uma seleção com 10 questões resolvidas sobre função afim, todas com enunciado completo, gráficos, interpretação matemática e solução passo a passo. Ideal para quem está se preparando para o ENEM, concursos e vestibulares. Entenda como aplicar a função do 1º grau em situações reais como tarifas, salários, consumo de água, interseção de retas e mais. Aprenda com exemplos visuais e explicações claras!
🧠 Mapas Mentais de MatemáticaQuestão 01. (UECE) Um equipamento eletrônico utilizado por uma indústria tem seu valor monetário continuamente reduzido em função do uso e do surgimento de novas tecnologias, dentre outros fatores. Se o valor monetário do equipamento decresce linearmente com o tempo, sabendo-se que foi adquirido há três anos pelo valor de R$ 180.000,00 e que hoje está avaliado em R$ 135.000,00, é correto afirmar que o valor monetário do equipamento daqui a dois anos será:
- a) R$ 105.000,00
- b) R$ 115.000,00
- c) R$ 108.000,00
- d) R$ 112.000,00
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos um equipamento que vale R$ 180.000,00 há 3 anos e hoje vale R$ 135.000,00. O valor diminui de forma linear, e queremos saber quanto valerá daqui a 2 anos (ou seja, daqui a 5 anos após a compra).
1) Cálculo da taxa de depreciação anual:
Em 3 anos, o equipamento perdeu:
$$ 180.000 – 135.000 = 45.000 $$
Logo, a depreciação anual é:
$$ \frac{45.000}{3} = 15.000 \text{ por ano} $$
2) Valor após 5 anos:
$$ \text{Valor final} = 180.000 – (5 \cdot 15.000) = 180.000 – 75.000 = 105.000 $$
✅ Conclusão:
- Valor do equipamento daqui a 2 anos: $$ R\$ 105.000,00 $$
- Alternativa correta: a)
Questão 02. (Enem/MEC) Muitas vezes o objetivo de um remédio é aumentar a quantidade de uma ou mais substâncias já existentes no corpo do indivíduo para melhorar as defesas do organismo. Depois de alcançar o objetivo, essa quantidade deve voltar ao normal.
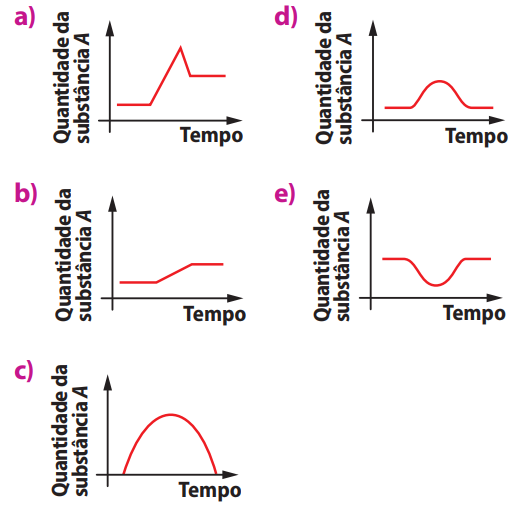
Se uma determinada pessoa ingere um medicamento para aumentar a concentração da substância A em seu organismo, a quantidade dessa substância no organismo da pessoa, em relação ao tempo, pode ser mais bem representada no gráfico:
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O medicamento é administrado para aumentar a substância A no corpo, mas essa quantidade deve voltar ao normal após cumprir sua função. Isso significa que o gráfico deve mostrar um aumento, seguido de uma queda até o nível inicial.
Análise das alternativas:
- a) Indica aumento e estabilização — não retorna ao normal.
- b) Aumento constante — não condiz com o retorno.
- c) Forma de parábola — boa opção, mas depende da interpretação do “nível normal”.
- d) Aumenta, atinge um pico e retorna ao valor inicial — correta.
- e) Variações desconexas — não representa bem o processo descrito.
✅ Conclusão:
- Gráfico que representa corretamente o comportamento da substância A: d)
Questão 03. (FEI-SP) Durante o tratamento térmico de uma peça metálica, sua temperatura varia de acordo com o gráfico abaixo.
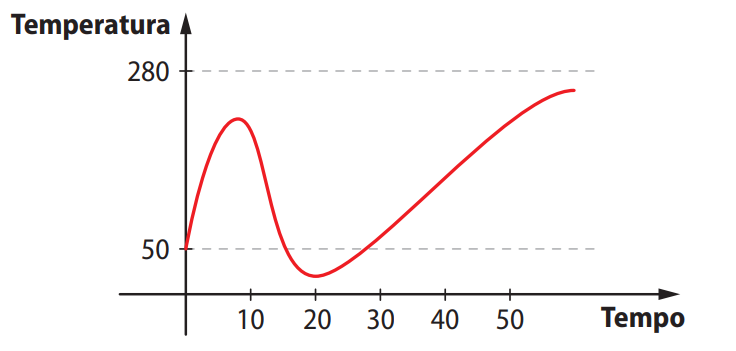
É válido afirmar:
- a) a partir do instante \( t = 10 \), as temperaturas são crescentes.
- b) a partir do instante \( t = 5 \), as temperaturas são decrescentes.
- c) a partir do instante \( t = 20 \), as temperaturas são crescentes.
- d) todas as temperaturas observadas são maiores do que 50.
- e) há um determinado valor de temperatura que foi observado em 5 instantes diferentes.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos observar o comportamento da temperatura da peça ao longo do tempo, analisando se ela está aumentando ou diminuindo em determinados intervalos, e verificar quais afirmações são verdadeiras com base no gráfico.
Análise das alternativas:
- a) Incorreta – A partir de \( t = 10 \) a curva ainda está em queda.
- b) Incorreta – A partir de \( t = 5 \), ainda há crescimento até próximo de \( t = 10 \).
- c) Correta – A partir de \( t = 20 \), a curva começa a crescer continuamente.
- d) Incorreta – O gráfico mostra valores abaixo de 50 entre \( t = 20 \) e \( t = 30 \).
- e) Incorreta – A função não apresenta um mesmo valor de temperatura em 5 instantes distintos.
✅ Conclusão:
- Alternativa correta: c)
Questão 04. (UEA-AM) A reta \( r \) passa pelos pontos \( (4, 6) \) e \( (0, -4) \) e intersecta o eixo das abscissas no ponto \( P \), conforme mostra a figura.
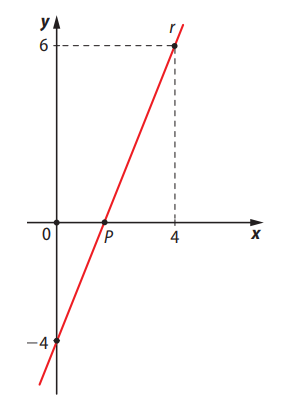
O valor da abscissa do ponto \( P \) é:
- a) \( 2 \)
- b) \( \frac{5}{2} \)
- c) \( \frac{3}{8} \)
- d) \( \frac{8}{5} \)
- e) \( \frac{3}{2} \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A reta passa por dois pontos conhecidos. Desejamos encontrar o ponto \( P \) onde ela cruza o eixo \( x \) (isto é, onde \( y = 0 \)).
1) Encontrar a equação da reta:
Usamos os pontos \( (0, -4) \) e \( (4, 6) \):
Coeficiente angular:
$$ m = \frac{6 – (-4)}{4 – 0} = \frac{10}{4} = \frac{5}{2} $$
Agora, aplicamos na equação geral da reta \( y = mx + b \):
Como passa por \( (0, -4) \), então \( b = -4 \).
Logo, a equação da reta é:
$$ y = \frac{5}{2}x – 4 $$
2) Calcular a abscissa do ponto \( P \):
No ponto \( P \), temos \( y = 0 \). Substituímos:
$$ 0 = \frac{5}{2}x – 4 $$
$$ \frac{5}{2}x = 4 $$
$$ x = \frac{4 \cdot 2}{5} = \frac{8}{5} $$
✅ Conclusão:
- Abscissa do ponto \( P \): $$ \frac{8}{5} $$
- Alternativa correta: d)
Questão 05. (Enem/MEC) Um anúncio oferece vagas para vendedores jovens:
VENDEDORES JOVENS
Fábrica de LONAS
Vendas no Atacado
10 vagas para estudantes,
18 a 20 anos, sem experiência.
Salário: R$ 300,00 fixo + comissão
de R$ 0,50 por m² vendido.
Contato: 0xx97 – 43421167 ou
atacadista@lonaboa.com.br
Na seleção para as vagas deste anúncio, propunha-se aos candidatos a seguinte questão:
Deveriam calcular seu salário no primeiro mês, se vendessem 500 m de tecido com largura de 1,40 m. No segundo mês, vendessem o dobro.
Foram bem-sucedidos os jovens que responderam, respectivamente:
- a) R$ 300,00 e R$ 500,00
- b) R$ 550,00 e R$ 850,00
- c) R$ 650,00 e R$ 1.000,00
- d) R$ 650,00 e R$ 1.300,00
- e) R$ 950,00 e R$ 1.900,00
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Salário fixo: R$ 300,00.
Comissão: R$ 0,50 por metro quadrado vendido.
No 1º mês: vendeu 500 m de comprimento com 1,40 m de largura.
1) Cálculo da área vendida no 1º mês:
$$ \text{Área} = 500 \times 1{,}4 = 700 \text{ m}^2 $$
Comissão no 1º mês:
$$ 700 \times 0{,}50 = R\$ 350,00 $$
Salário total:
$$ 300 + 350 = R\$ 650,00 $$
2) No 2º mês: vende o dobro → 1000 m × 1,40 m:
$$ \text{Área} = 1000 \times 1{,}4 = 1400 \text{ m}^2 $$
Comissão:
$$ 1400 \times 0{,}50 = R\$ 700,00 $$
Salário total:
$$ 300 + 700 = R\$ 1.000,00 $$
✅ Conclusão:
- 1º mês: R$ 650,00
- 2º mês: R$ 1.000,00
- Alternativa correta: c)
Questão 06. (Epcar-MG) Para fazer uma instalação elétrica em sua residência, Otávio contatou dois eletricistas.
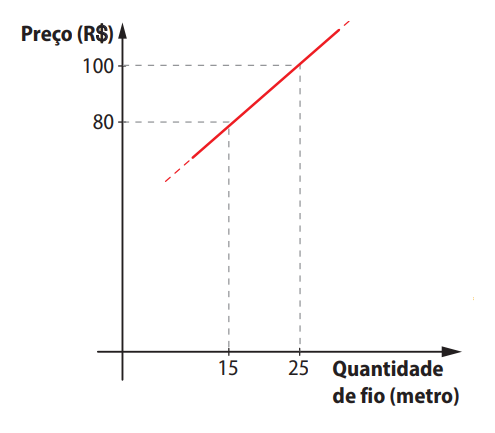
O Sr. Luiz cobra uma parte fixa mais uma taxa proporcional aos metros de fio. O gráfico abaixo mostra a relação entre o custo e a quantidade de fio:
Já o Sr. José cobra apenas R$ 4,50 por metro de fio utilizado, sem taxa fixa.
Com relação às informações acima, é correto afirmar que:
- a) o valor da parte fixa cobrada pelo Sr. Luiz é maior do que R$ 60,00.
- b) o Sr. Luiz cobra mais de R$ 2,50 por metro de fio instalado.
- c) sempre será mais vantajoso contratar o serviço do Sr. José.
- d) se forem gastos 20 m de fio não haverá diferença de valor total cobrado entre os eletricistas.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos dois pontos do gráfico de Sr. Luiz:
- \( (15, 85) \): 15 m → R$ 85,00
- \( (25, 100) \): 25 m → R$ 100,00
Vamos determinar a equação da função custo:
1) Cálculo do coeficiente angular:
$$ a = \frac{100 – 85}{25 – 15} = \frac{15}{10} = 1{,}5 $$
Ou seja, ele cobra R$ 1,50 por metro de fio.
2) Determinar a parte fixa:
Usando o ponto \( (15, 85) \):
$$ 85 = 1{,}5 \cdot 15 + b \Rightarrow 85 = 22{,}5 + b \Rightarrow b = 62{,}5 $$
A equação do custo do Sr. Luiz é:
$$ C(x) = 1{,}5x + 62{,}5 $$
3) Comparando com Sr. José:
Sr. José: \( C(x) = 4{,}5x \)
Igualando os dois custos:
$$ 1{,}5x + 62{,}5 = 4{,}5x $$
$$ 62{,}5 = 3x \Rightarrow x = \frac{62{,}5}{3} = 20{,}83… $$
Ou seja, o custo será igual aproximadamente quando forem gastos 20,83 m de fio.
4) Para 20 metros:
- Sr. Luiz: \( C = 1{,}5 \cdot 20 + 62{,}5 = 30 + 62{,}5 = 92{,}5 \)
- Sr. José: \( C = 4{,}5 \cdot 20 = 90 \)
Portanto, por volta de 20 m os valores são praticamente iguais.
✅ Conclusão:
- Alternativa correta: d)
Questão 07. (UFPI) A função real de variável real, definida por:
$$ f(x) = (3 – 2a) \cdot x + 2 $$
é crescente quando:
- a) \( a > 0 \)
- b) \( a < \frac{3}{2} \)
- c) \( a = \frac{3}{2} \)
- d) \( a > \frac{3}{2} \)
- e) \( a < 3 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função afim \( f(x) = mx + b \) é crescente quando o coeficiente angular \( m > 0 \).
No caso, o coeficiente angular é:
$$ m = 3 – 2a $$
1) Impor a condição de crescimento:
$$ 3 – 2a > 0 $$
$$ -2a > -3 $$
Multiplicando por (-1) e invertendo o sinal:
$$ 2a < 3 \Rightarrow a < \frac{3}{2} $$
✅ Conclusão:
- Para que a função seja crescente: \( a < \frac{3}{2} \)
- Alternativa correta: b)
Questão 08. (Enem/MEC) Uma fatura mensal de água é composta por uma taxa fixa, independente do gasto, mais uma parte proporcional ao volume de água consumido.
O gráfico relaciona o valor da fatura com o volume de água (em m³) consumido por uma residência no mês de novembro:
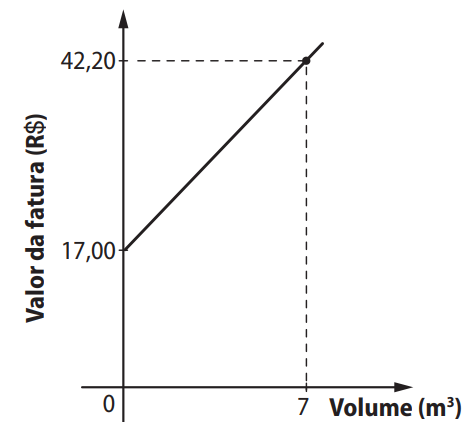
Observa-se que nesse mês houve um consumo de 7 m³. Sabe-se que em dezembro o consumo dobrou. O valor da fatura referente ao mês de dezembro foi:
-
a) superior a R$ 65,00 e inferior a R$ 70,00
b) superior a R$ 80,00 e inferior a R$ 85,00
c) superior a R$ 90,00 e inferior a R$ 95,00
d) superior a R$ 95,00
e) inferior a R$ 55,00
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Do gráfico, temos que para \( 7 \, m^3 \), a fatura foi de R$ 42,20. Para \( 0 \, m^3 \), o valor é R$ 17,00. Isso indica uma função afim:
1) Determinar a função:
Dois pontos: \( (0, 17) \) e \( (7, 42{,}20) \)
Coeficiente angular:
$$ a = \frac{42{,}20 – 17}{7 – 0} = \frac{25{,}20}{7} \approx 3{,}60 $$
Assim, a função é:
$$ f(x) = 3{,}60x + 17 $$
2) Para 14 m³ (dezembro):
Dobro de 7 m³ → \( x = 14 \)
$$ f(14) = 3{,}60 \cdot 14 + 17 = 50{,}40 + 17 = 67{,}40 $$
✅ Conclusão:
- Fatura de dezembro: R$ 67,40
- Faixa correta: a) superior a R$ 65,00 e inferior a R$ 70,00
Questão 09. (IFPE) Os volumes de água \( V \), medidos em litros, em dois reservatórios \( A \) e \( B \), variam em função do tempo \( t \), em minutos, conforme as expressões:
$$ V_A(t) = 200 + 3t \quad \text{e} \quad V_B(t) = 5000 – 3t $$
Determine o instante \( t \) em que os dois reservatórios terão o mesmo volume.
- a) \( t = 500 \) minutos
- b) \( t = 600 \) minutos
- c) \( t = 700 \) minutos
- d) \( t = 800 \) minutos
- e) \( t = 900 \) minutos
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos encontrar o valor de \( t \) que torna os volumes iguais, ou seja:
$$ V_A(t) = V_B(t) $$
1) Igualando as expressões:
$$ 200 + 3t = 5000 – 3t $$
2) Somando \( 3t \) nos dois lados:
$$ 200 + 6t = 5000 $$
3) Subtraindo 200:
$$ 6t = 4800 $$
4) Dividindo por 6:
$$ t = \frac{4800}{6} = 800 $$
✅ Conclusão:
- Instante em que os volumes se igualam: \( t = 800 \) minutos
- Alternativa correta: d)
Questão 10. (UEA-AM) Considere as funções polinomiais do 1º grau:
$$ f(x) = 2x + 3 \quad \text{e} \quad g(x) = -x + 6 $$
Sobre essas funções, afirma-se que:
- a) possuem pontos de máximo.
- b) são crescentes.
- c) possuem domínios diferentes.
- d) têm o ponto \( (1, 5) \) em comum.
- e) suas representações gráficas não se intersectam.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
As funções são do 1º grau. Vamos verificar se elas se intersectam e se há algum ponto em comum.
1) Avaliar os valores em \( x = 1 \):
Para \( f(x) \):
$$ f(1) = 2 \cdot 1 + 3 = 5 $$
Para \( g(x) \):
$$ g(1) = -1 + 6 = 5 $$
Logo, ambas passam pelo ponto \( (1, 5) \).
2) Análise das demais alternativas:
- a) Incorreta – funções do 1º grau não têm ponto de máximo.
- b) Incorreta – apenas \( f(x) \) é crescente; \( g(x) \) é decrescente.
- c) Incorreta – ambas têm o mesmo domínio: \( \mathbb{R} \).
- d) Correta
- e) Incorreta – como têm ponto em comum, suas retas se cruzam.
✅ Conclusão:
- Ponto comum: \( (1, 5) \)
- Alternativa correta: d)