Função bijetiva
Definição formal, relação com inversa, testes práticos, exemplos e exercícios resolvidos.
Uma função \(f:A\to B\) é bijetiva quando é simultaneamente injetiva e sobrejetiva. Isso estabelece uma correspondência um-para-um e sobre entre \(A\) e \(B\).
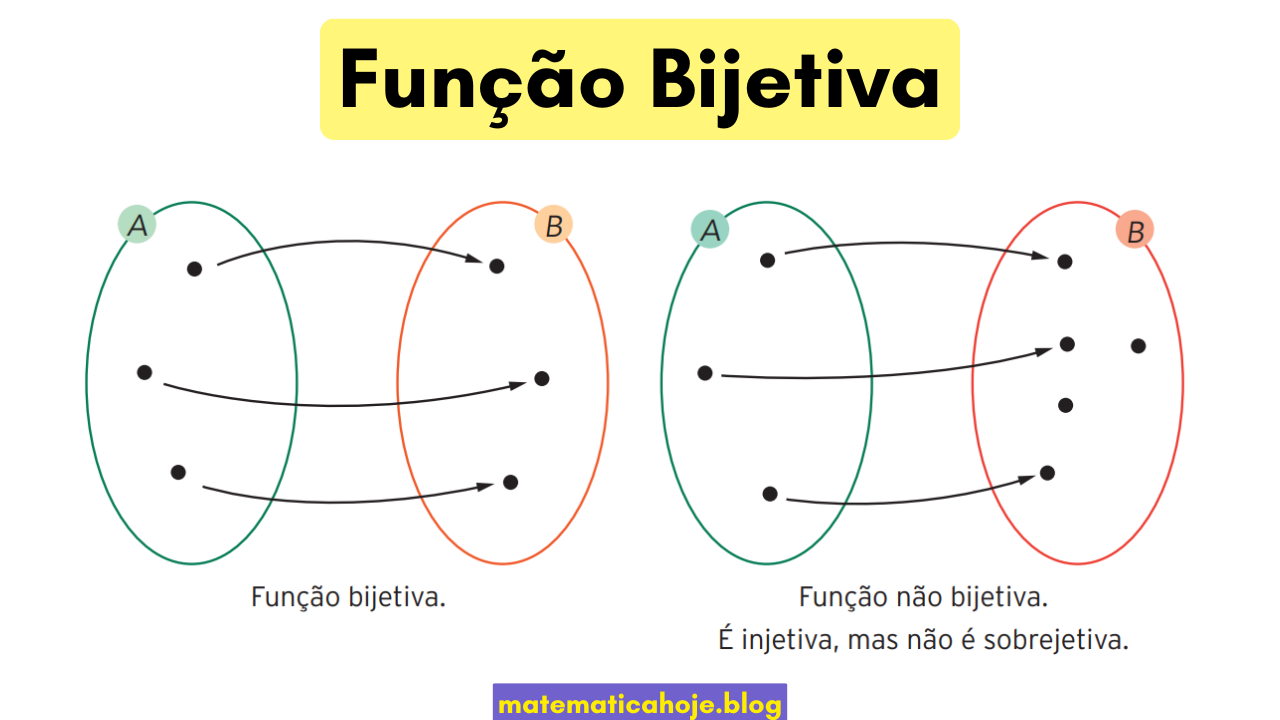
Definições e propriedades-chave
- Composição: se \(f\) e \(g\) são bijetivas, \(g\circ f\) é bijetiva e \((g\circ f)^{-1}=f^{-1}\circ g^{-1}\).
- Conjuntos finitos: existe bijeção \(A\leftrightarrow B\) \(\iff\) \(|A|=|B|\). Em \(A\) finito, bijeções \(A\to A\) são permutações.
- Gráfico: passa nos dois testes: reta horizontal (injeção) e cobertura do contradomínio (sobrejeção).
Testes práticos
- Linear \(y=ax+b\) com \(a\neq0\) é bijetiva \(\mathbb{R}\to\mathbb{R}\); inversa \(f^{-1}(y)=\dfrac{y-b}{a}\).
- Monotonicidade + limites: se \(f\) é contínua, estritamente monótona em \(\mathbb{R}\) e \(\lim_{x\to\pm\infty}f(x)=\pm\infty\), então \(f:\mathbb{R}\to\mathbb{R}\) é bijetiva (ex.: \(x^3+2x\)).
- Escolha do contradomínio: \(e^x\) é bijetiva \(\mathbb{R}\to(0,\infty)\) (inversa \(\ln x\)), mas não é bijetiva \(\mathbb{R}\to\mathbb{R}\).
- Restrição do domínio: \(x^2\) não é bijetiva em \(\mathbb{R}\to\mathbb{R}\), mas é bijetiva \([0,\infty)\to[0,\infty)\) (inversa \(\sqrt{x}\)).
Exemplos resolvidos
1) Linear
\(f(x)=3x-5\) em \(\mathbb{R}\). É estritamente crescente e cobre \(\mathbb{R}\).\ Inversa: \(y=3x-5\Rightarrow x=\dfrac{y+5}{3}\Rightarrow f^{-1}(y)=\dfrac{y+5}{3}\).
2) Exponencial
\(g(x)=e^x\) é bijetiva \(\mathbb{R}\to(0,\infty)\). Inversa \(g^{-1}(y)=\ln y\).
3) Quadrática com restrição
\(h(x)=x^2\) em \(A=[0,\infty)\) para \(B=[0,\infty)\). É crescente e \(\operatorname{Im}(h)=B\). Inversa \(h^{-1}(y)=\sqrt{y}\).
4) Transformação de Möbius
\(F(x)=\dfrac{ax+b}{cx+d}\) com \(ad-bc\neq0\). Bijeção entre \(A=\mathbb{R}\setminus\{-d/c\}\) e \(B=\mathbb{R}\setminus\{a/c\}\) com \[ F^{-1}(y)=\frac{dy-b}{-cy+a}. \]
Quadro-resumo
| Ponto | Como verificar | Observação |
|---|---|---|
| Injetividade | Reta horizontal / \(f'(x)\) sem trocar sinal | Nenhuma imagem repetida |
| Sobrejetividade | Resolver \(f(x)=y\) para todo \(y\in B\) | \(\operatorname{Im}(f)=B\) |
| Inversa | Isolar \(x\) em \(y=f(x)\) | Existência \(\iff\) bijetividade |
| Composição | \(f,g\) bijetivas \(\Rightarrow g\circ f\) bijetiva | \((g\circ f)^{-1}=f^{-1}\circ g^{-1}\) |
| Conj. finitos | Comparar \(|A|\) e \(|B|\) | Bijeção \(\iff |A|=|B|\) |
Exercícios (múltipla escolha) com solução
1) Quais das funções abaixo são bijetivas nos domínios/contradomínios indicados?
- \(f(x)=2x+1:\ \mathbb{R}\to\mathbb{R}\)
- \(g(x)=x^2:\ \mathbb{R}\to\mathbb{R}\)
- \(h(x)=e^x:\ \mathbb{R}\to(0,\infty)\)
- \(p(x)=|x|:\ [0,\infty)\to[0,\infty)\)
- Apenas \(f\) e \(h\)
- Apenas \(g\) e \(p\)
- \(f\), \(h\) e \(p\)
- Todas
Ver solução
2) A inversa de \(f(x)=3x-5\) é:
- \(f^{-1}(x)=3x-5\)
- \(f^{-1}(x)=\dfrac{x-5}{3}\)
- \(f^{-1}(x)=\dfrac{x+5}{3}\)
- \(f^{-1}(x)=\dfrac{5-x}{3}\)
Ver solução
3) \(q(x)=x^3+2\) em \(\mathbb{R}\to\mathbb{R}\) é:
- Somente injetiva
- Somente sobrejetiva
- Bijetiva
- Nenhuma
Ver solução
4) Para tornar \(x^2\) bijetiva com inversa \(f^{-1}(y)=\sqrt{y}\), escolha domínio e contradomínio:
- \(\mathbb{R}\to\mathbb{R}\)
- \(\mathbb{R}\to[0,\infty)\)
- \([0,\infty)\to[0,\infty)\)
- \((-\infty,0]\to[0,\infty)\)
Ver solução
5) Se \(f\) e \(g\) são bijetivas, então \((g\circ f)^{-1}\) é:
- \(g^{-1}\circ f^{-1}\)
- \(f^{-1}\circ g^{-1}\)
- \(f\circ g\)
- \(g\circ f\)
Ver solução
6) Em conjuntos finitos, existe bijeção \(A\to B\) se, e somente se:
- \(|A|\ge|B|\)
- \(|A|\le|B|\)
- \(|A|=|B|\)
- Sempre existe
Ver solução
Continue estudando
• Função injetiva
• Função sobrejetiva
• Gráfico de uma Função
• Domínio & Imagem
• Coleção 10 eBooks • eBook Fórmulas Matemática • Banco de Questões













