Função do Segundo Grau: Concavidade, Coeficientes e Gráfico
A função do segundo grau, também chamada de função quadrática, descreve uma parábola no plano cartesiano e aparece com frequência no ENEM, vestibulares e concursos. Este guia visual explica o papel dos coeficientes a, b e c e inclui exercícios com soluções.
Forma geral
$$ f(x) = ax^2 + bx + c, \quad a \neq 0 \quad (a,b,c \in \mathbb{R}) $$
📘 Coeficientes e efeitos no gráfico
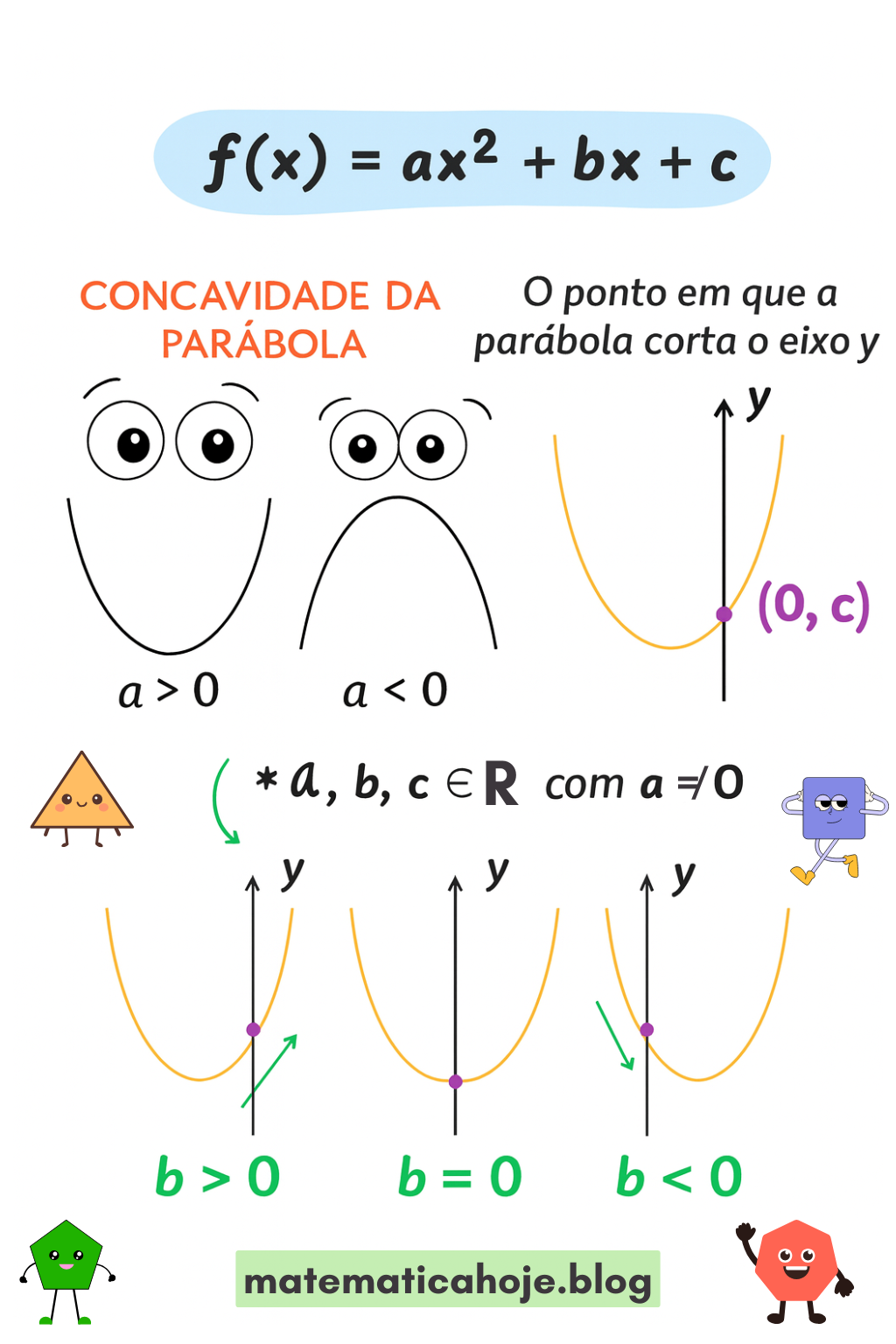
- Coeficiente a: determina a concavidade da parábola.
- Se \(a>0\): parábola voltada para cima.
- Se \(a<0\): parábola voltada para baixo.
- Coeficiente b: desloca o vértice horizontalmente (inclinação do eixo de simetria).
- \(b>0\) → vértice desloca à esquerda do eixo y.
- \(b=0\) → vértice sobre o eixo y.
- \(b<0\) → vértice desloca à direita.
- Coeficiente c: intersecção com o eixo y: $$ f(0) = c \Rightarrow (0,c). $$
Todas as fórmulas essenciais em 1 arquivo para estudo e revisão!
🧠 Exemplos rápidos
\(a=2 \Rightarrow\) concavidade para cima; \(b=-4\Rightarrow\) vértice à direita;
\(c=1 \Rightarrow (0,1)\) no eixo y.
\(a=-1 \Rightarrow\) concavidade para baixo; \(b=3\Rightarrow\) vértice à esquerda;
\(c=2 \Rightarrow (0,2)\) no eixo y.
Quer revisar por mapas? Veja os Mapas Mentais de Matemática. Procura lista grande para treinar? Conheça o Banco de Questões ou a Coleção com 10 eBooks.
📝 Exercícios sobre Função do Segundo Grau
Com gabarito e solução passo a passo
👀 Ver solução
A concavidade depende apenas do sinal de \(a\).
Se \(a>0\) então a parábola é côncava para cima. Alternativa C.
👀 Ver solução
Basta calcular \(f(0)\):
\(f(0)=3\cdot0^2 -2\cdot0 + 5\) = 0 + 0 + 5 = 5.
Logo o ponto é \((0,5)\). Alternativa C.
👀 Ver solução
Para \(b=0\), o eixo de simetria é \(x=-\frac{b}{2a}=0\), ou seja, sobre o eixo y.
Alternativa B.
👀 Ver solução passo a passo
Substitua \(x=0\):
\(g(0)=-2\cdot0^2+4\cdot0-3\)
\(= 0 + 0 – 3\)
\(= -3\).
Logo, o ponto é (0, -3).
👀 Ver solução passo a passo
O eixo de simetria é \(x_v=-\dfrac{b}{2a}\).
Como o vértice está à direita do eixo y, então \(x_v>0\).
\(x_v>0 \Rightarrow -\dfrac{b}{2a}>0\). Como \(a=2>0\), temos \(-b>0 \Rightarrow b<0\).
Logo, b é negativo.
B) para baixo; vértice à esquerda
C) para baixo; vértice sobre o eixo y
D) para cima; vértice à esquerda
👀 Ver solução
\(a=-1<0\Rightarrow\) concavidade para baixo.
\(b=-6<0\Rightarrow\) vértice desloca-se para a direita? Não: lembre que \(b<0\) → vértice à direita. Ops, vamos checar pelo eixo de simetria:
\(x_v=-\dfrac{b}{2a}=-\dfrac{-6}{2\cdot(-1)}=\dfrac{6}{-2}=-3\) (negativo → à esquerda do eixo y).
Logo: para baixo; vértice à esquerda. Alternativa B.
👀 Ver solução passo a passo
Se \((1,4)\) está no gráfico, então \(f(1)=4\).
\(f(1)=1^2-2\cdot1+c\)
\(=1-2+c\)
\(= -1 + c\).
Igualando: \(-1+c = 4 \Rightarrow c = 5\).
🔗 Continue estudando
- Mapas Mentais de Matemática
- Matemática para o ENEM
- Coleção 10 eBooks
- Banco de Questões de Matemática
- eBook Fórmulas Matemática (PDF)
Gostou do material? Compartilhe com a turma e salve este post para revisão! 💙





















