Função Exponencial
Descubra como funciona a função exponencial, suas propriedades, gráficos e aplicações na matemática e no cotidiano.
Definição: A função exponencial é toda função da forma:
\[
f(x) = a^x \quad (a > 0, \; a \neq 1)
\]
onde a variável \(x\) aparece no expoente.
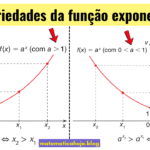
1) Propriedades da função exponencial
- O domínio é \(\mathbb{R}\) (todos os números reais).
- A imagem é \((0, +\infty)\).
- Sempre é positiva: \(f(x) > 0\).
- Possui uma assíntota horizontal no eixo \(x\).
- Se \(a > 1\), a função é crescente. Se \(0 < a < 1\), é decrescente.
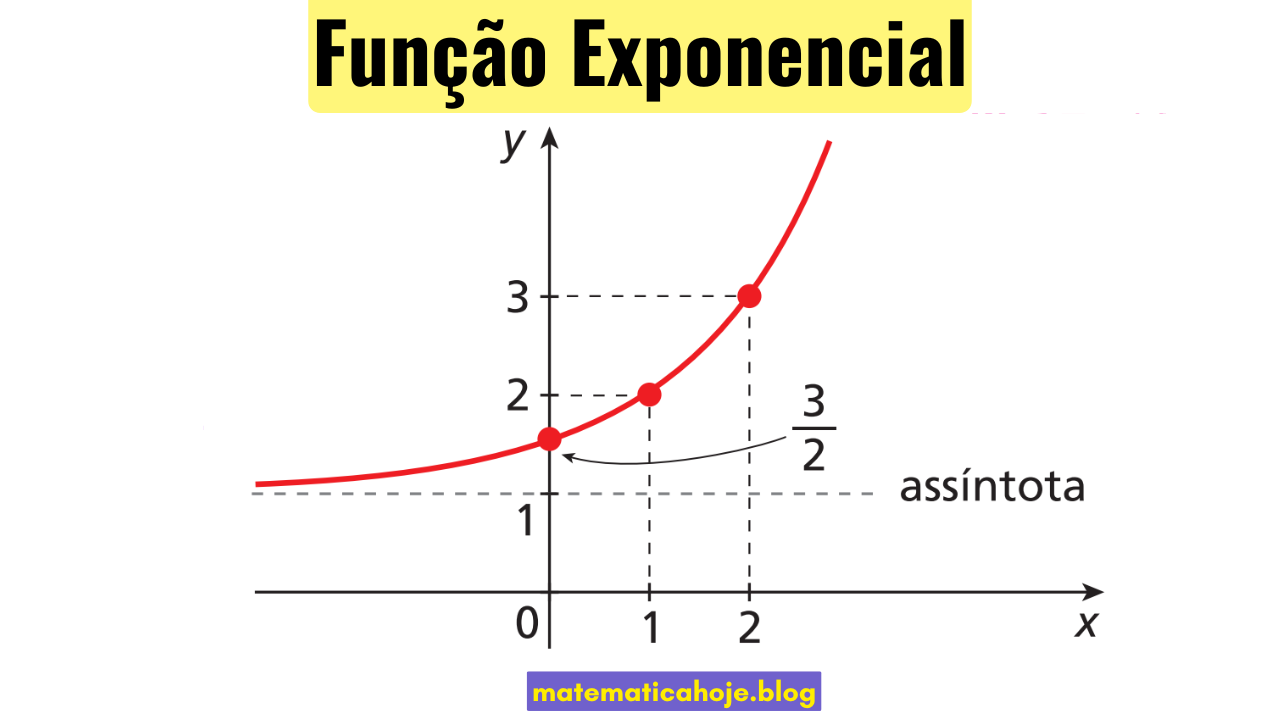
2) Exemplo prático
Considere \(f(x) = \left(\tfrac{3}{2}\right)^x\).
– \(f(0) = 1\)
– \(f(1) = \tfrac{3}{2}\)
– \(f(2) = \left(\tfrac{3}{2}\right)^2 = \tfrac{9}{4} = 2,25\)
– \(f(3) = \left(\tfrac{3}{2}\right)^3 = \tfrac{27}{8} \approx 3,375\)
O gráfico mostra claramente o crescimento acelerado.
3) Aplicações no cotidiano
- Juros compostos em matemática financeira.
- Crescimento populacional.
- Decaimento radioativo em física.
- Propagação de vírus em epidemiologia.
4) Exercícios resolvidos
Exemplo 1: Determine \(f(4)\) para a função \(f(x) = 2^x\).
\[
f(4) = 2^4 = 16
\]
Resposta: \(f(4) = 16\).
Exemplo 2: Resolva a equação exponencial \(3^x = 81\).
\[
3^x = 81 \quad \Rightarrow \quad 81 = 3^4 \quad \Rightarrow \quad x = 4
\]
Resposta: \(x = 4\).
📘 Aprenda mais sobre funções com nosso material exclusivo!
Baixe grátis o eBook Fórmulas Matemática
Baixe grátis o eBook Fórmulas Matemática
5) Exercícios propostos
- Calcule \(f(-2)\) para a função \(f(x) = 5^x\).
- Resolva a equação exponencial \(2^x = 64\).
- Determine se a função \(f(x) = \left(\tfrac{1}{2}\right)^x\) é crescente ou decrescente.