Função Exponencial: Definição, Gráficos e Exercícios Resolvidos

A função exponencial é um tipo especial de função que descreve diversos fenômenos naturais e econômicos, como o crescimento populacional, o decaimento radioativo e os juros compostos. Entender seu comportamento é essencial no estudo da matemática aplicada e no preparo para vestibulares e concursos.

O que é uma Função Exponencial?

Chamamos de função exponencial toda função da forma:

f(x) = a^x

Onde:

• a é a base da função, com a > 0 e a ≠ 1;
• x é a variável no expoente.

Exemplos:

• f(x) = 2^x
• f(x) = (1/2)^x
• f(x) = e^x (função exponencial natural, onde e ≈ 2,718)

Características da Função Exponencial

• O gráfico nunca toca o eixo x (y nunca é zero);
• O ponto (0, 1) sempre pertence ao gráfico;
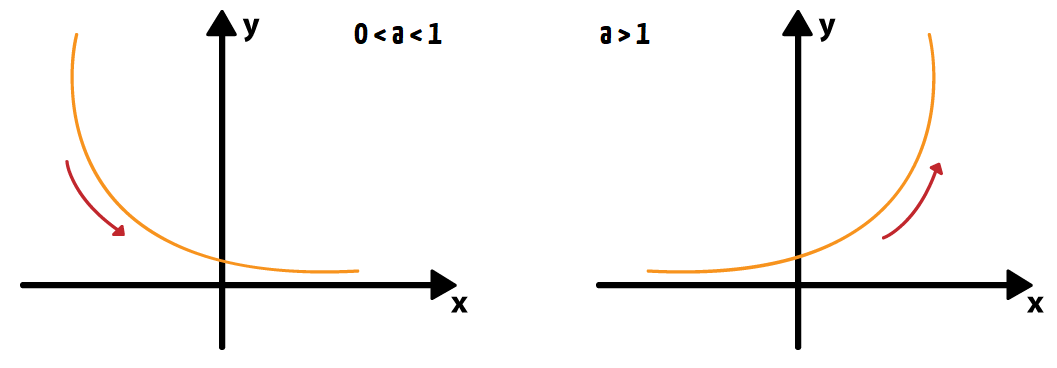
• Se a > 1, a função é crescente;
• Se 0 < a < 1, a função é decrescente;
• O domínio é ℝ (todos os reais);
• A imagem é y > 0.

Gráficos da Função Exponencial

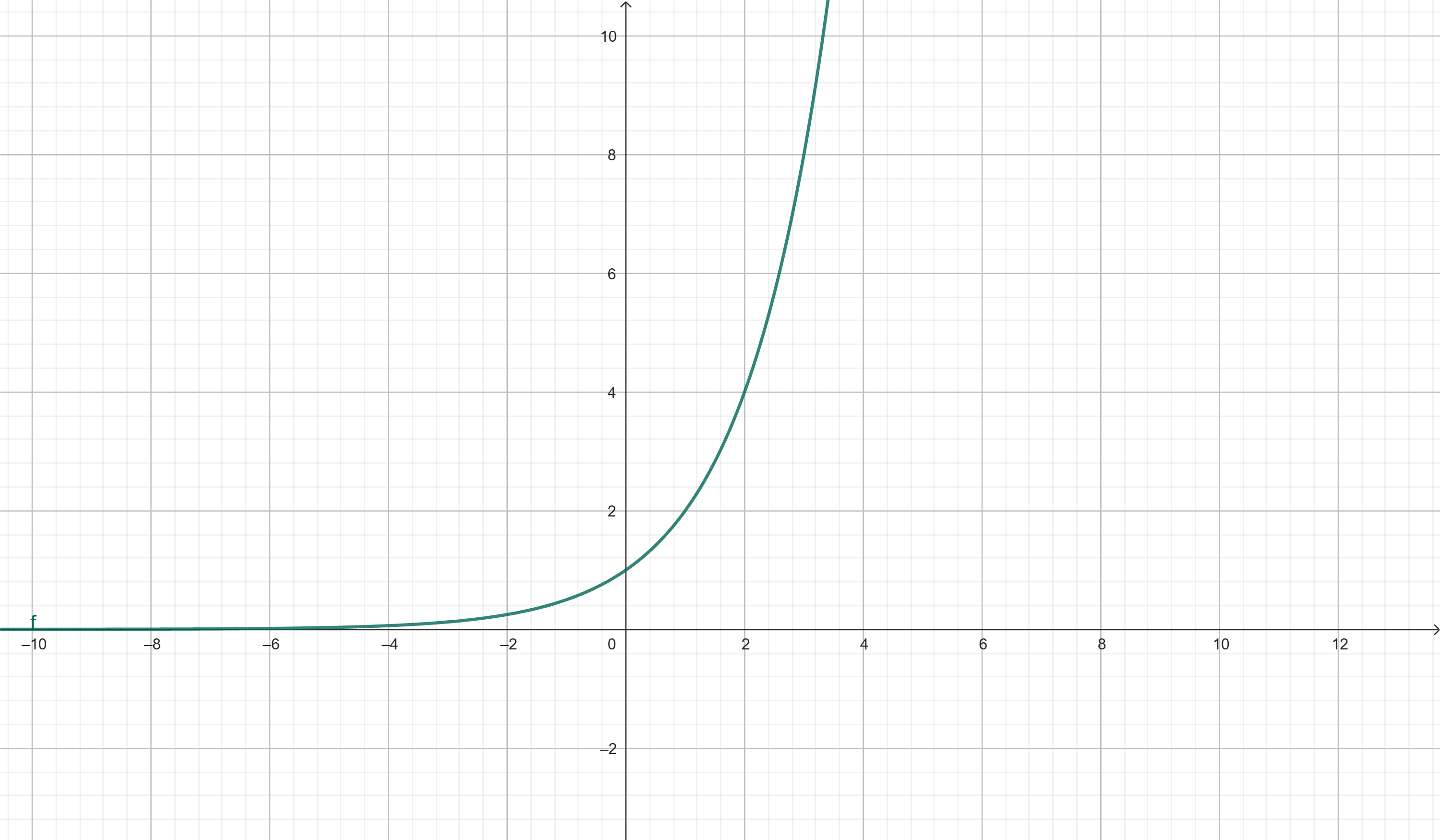
Exemplo 1: f(x) = 2^x

• Crescente
• Ponto notável: f(0) = 1

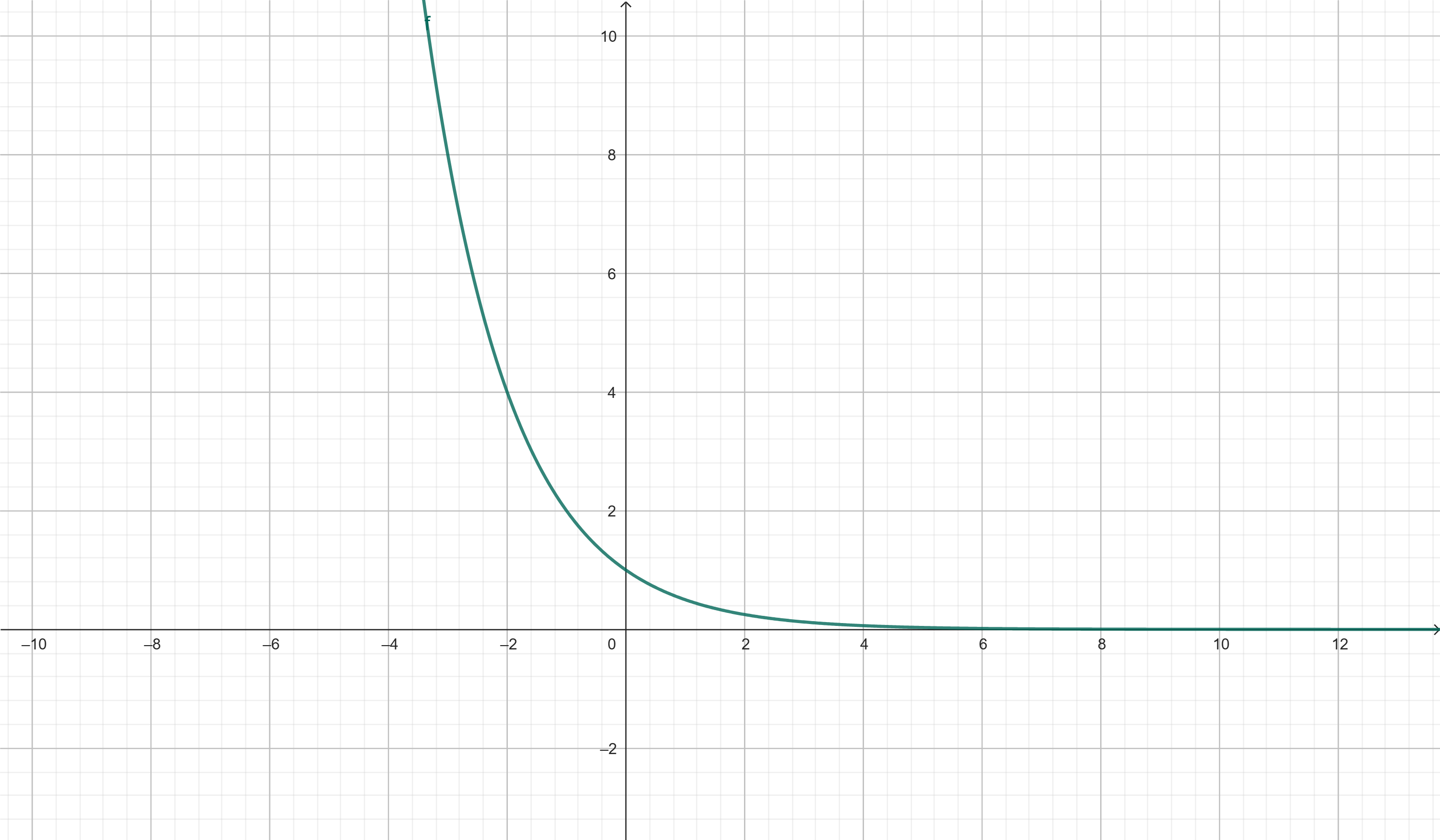
Exemplo 2: f(x) = (1/2)^x

• Decrescente
• Ponto notável: f(0) = 1

Gráficos da Função Exponencial

Transformações da Função Exponencial

Podemos aplicar transformações como:

• f(x) = a^{x + c}: deslocamento horizontal
• f(x) = a^x + d: deslocamento vertical
• f(x) = -a^x: simetria em relação ao eixo x

Exercícios Resolvidos

Exercício 1

Calcule f(3) na função f(x) = 2^x

Solução:
f(3) = 2³ = 8

Exercício 2

Determine se a função f(x) = (1/3)^x é crescente ou decrescente

Solução:
Como 0 < 1/3 < 1, a função é decrescente.

Exercício 3

Qual é a imagem da função f(x) = 5^x?

Solução:
Como uma função exponencial sempre retorna valores positivos, a imagem é f(x) ∈ (0, ∞)

Exercício 4

Esboce o gráfico da função f(x) = 2^x + 3

Solução:
Trata-se do gráfico de f(x) = 2^x, deslocado 3 unidades para cima. A assíntota horizontal passa a ser y = 3.

Exercício 5

Resolva a equação: 3^x = 81

Solução:
81 = 3⁴ ⇒ 3^x = 3⁴ → x = 4

Conclusão

A função exponencial é essencial para o estudo de crescimento e decaimento em diversas áreas do conhecimento. Ao entender seu gráfico, propriedades e comportamento, o estudante estará apto a enfrentar questões de nível médio e superior com mais segurança.

Continue estudando com nossos conteúdos exclusivos e veja também os artigos sobre Função Logarítmica e Função Racional.