Função Inversa — Definição, Passo a Passo, Gráficos e Exercícios

Função Inversa — Definição, Passo a Passo, Gráficos e Exercícios Resolvidos

Função Inversa — Definição, Passo a Passo, Gráficos e Exercícios

Aprenda quando a inversa existe, como calculá-la, como interpretar o gráfico e pratique com exemplos e exercícios (com gabarito).

📌 Mapas Mentais 🗂️ Banco de Questões

Capa ilustrativa: função e sua inversa simétricas em relação à reta y = x — Figura: gráficos de \(f\) e \(f^{-1}\) refletidos na reta \(y=x\).

Resumo rápido

Condição de existência: \(f\) deve ser bijetora (pelo menos injetora no domínio considerado).
Definição: \(f^{-1}\) é tal que \(f(f^{-1}(x)) = x\) e \(f^{-1}(f(x)) = x\).
Passos para achar \(f^{-1}\): (1) troque \(f(x)\) por \(y\); (2) isole \(x\) em função de \(y\); (3) troque \(y\) por \(x\) e nomeie \(f^{-1}(x)\).
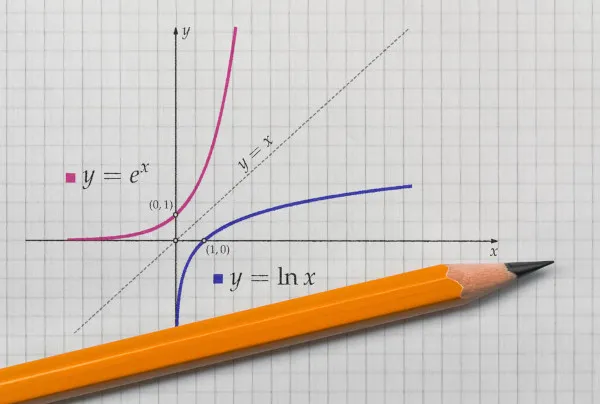
Gráfico: \(f\) e \(f^{-1}\) são simétricas em relação a \(y=x\).
Exemplos-chave: \(f(x)=ax+b\Rightarrow f^{-1}(x)=\dfrac{x-b}{a}\) (\(a\neq0\)); \(a^x \leftrightarrow \log_a x\) (\(a>0, a\neq1\)).

1) O que é função inversa?

Intuitivamente, a função inversa “desfaz” a ação de \(f\). Se \(f\) leva \(x\) em \(y\), então \(f^{-1}\) leva \(y\) de volta em \(x\). Formalmente, \(f^{-1}\) existe quando \(f\) é bijetora entre o domínio e a imagem.

Em muitos casos, restringimos o domínio de \(f\) para torná-la injetora e assim garantir a existência de \(f^{-1}\) (ex.: quadrática com domínio \(x\ge 0\) ou \(x\le 0\)).

2) Definição e condições

Injetividade: valores distintos de entrada não podem produzir a mesma saída.
Sobrejetividade: toda saída no contradomínio deve ser atingida por algum \(x\).
Bijetividade: injetiva + sobrejetiva → inversa bem definida.

Leituras relacionadas: Funções • Função composta

3) Teste da reta horizontal

Graficamente, uma função é injetiva se qualquer reta horizontal intercepta o gráfico no máximo uma vez. Se não for injetiva, restrinja o domínio.

Exemplo: \(f(x)=x^2\) não é injetiva em \(\mathbb{R}\), mas é injetiva em \([0,\infty)\) ou em \((-\infty,0]\).

4) Como encontrar a inversa (passo a passo)

Escreva \(y = f(x)\).
Resolva para \(x\) em função de \(y\).
Troque \(y\) por \(x\) e nomeie a expressão como \(f^{-1}(x)\).
Verifique: calcule \(f(f^{-1}(x))\) e \(f^{-1}(f(x))\).

5) Relação entre gráficos

Os gráficos de \(f\) e \(f^{-1}\) são reflexos um do outro na reta \(y=x\). Interseções de \(f\) com \(y=x\) (pontos onde \(f(x)=x\)) são pontos fixos que pertencem a ambas.

6) Composição \(f\circ f^{-1}\) e \(f^{-1}\circ f\)

Se \(f^{-1}\) existe, então \(f(f^{-1}(x))=x\) (para \(x\) no domínio de \(f^{-1}\)) e \(f^{-1}(f(x))=x\) (para \(x\) no domínio de \(f\)).

7) Exemplos resolvidos

Exemplo 1 — Linear: \(f(x)=2x+3\)

Passos: \(y=2x+3 \Rightarrow x=\dfrac{y-3}{2}\). Trocando \(y\) por \(x\):

\[\boxed{f^{-1}(x)=\frac{x-3}{2}}\]

Checagem: \(f(f^{-1}(x))=2\cdot\frac{x-3}{2}+3=x\).

Exemplo 2 — Quadrática com restrição: \(f(x)=x^2\), \(x\ge 0\)

Com \(x\ge 0\), \(f\) é injetiva. Faça \(y=x^2 \Rightarrow x=\sqrt{y}\) (raiz principal).

\[\boxed{f^{-1}(x)=\sqrt{x}},\ \ x\ge 0.\]

Sem restrição, a inversa não é função (retas horizontais cortam o gráfico em dois pontos).

Exemplo 3 — Exponencial e Logaritmo: \(f(x)=a^x\) (\(a>0, a\neq1\))

\(y=a^x \Rightarrow x=\log_a y\). Logo,

\[\boxed{f^{-1}(x)=\log_a x},\ \ x>0.\]

Aprofunde em: Função exponencial e Função logarítmica.

8) Casos clássicos

Afim: \(f(x)=ax+b \Rightarrow f^{-1}(x)=\dfrac{x-b}{a}\), \(a\neq0\).
Potência par (com restrição): \(x^2,\ x\ge0 \Rightarrow \sqrt{x}\).
Potência ímpar: \(x^3 \Rightarrow \sqrt[3]{x}\) (já é bijetora em \(\mathbb{R}\)).

9) Dicas práticas

Antes de isolar, verifique se a função é injetiva (ou restrinja o domínio).
Nos logs e expoentes, cuide do domínio (\(x>0\) para log).
Use a composição como checagem final.

10) Exercícios resolvidos

Exercício R1 — Encontre a inversa de \(f(x)=\dfrac{3x-5}{2}\)

\(y=\dfrac{3x-5}{2}\Rightarrow 2y=3x-5 \Rightarrow 3x=2y+5 \Rightarrow x=\dfrac{2y+5}{3}\).

\[\boxed{f^{-1}(x)=\frac{2x+5}{3}}\]

Exercício R2 — Inversa de \(f(x)=\dfrac{x+1}{x-2}\) (domínio \(x\neq2\))

\(y=\dfrac{x+1}{x-2}\Rightarrow y(x-2)=x+1 \Rightarrow yx-2y=x+1\Rightarrow yx-x=2y+1\Rightarrow x(y-1)=2y+1\Rightarrow x=\dfrac{2y+1}{y-1}.\)

\[\boxed{f^{-1}(x)=\frac{2x+1}{x-1}}\] (domínio \(x\neq1\)).

Exercício R3 — Quadrática restrita: \(f(x)=x^2-6x+9=(x-3)^2\), com \(x\ge 3\)

\(y=(x-3)^2\Rightarrow x-3=\sqrt{y}\) (ramo principal, pois \(x\ge3\)) \(\Rightarrow x=3+\sqrt{y}\).

\[\boxed{f^{-1}(x)=3+\sqrt{x}},\ \ x\ge0.\]

11) Exercícios propostos

Determine \(f^{-1}(x)\) para \(f(x)=5x-7\).
Encontre a inversa (se existir) de \(f(x)=x^2-4\) em \((-\infty,0]\) e em \([0,\infty)\).
Para \(f(x)=\dfrac{2x+3}{x-1}\), ache \(f^{-1}(x)\) e indique o domínio.
Mostre que \(f(x)=x^3+1\) é bijetora em \(\mathbb{R}\) e obtenha \(f^{-1}(x)\).
Se \(f(x)=2^x\), verifique que \(f^{-1}(x)=\log_2 x\) e indique domínio/contradomínio.

Gabarito:

\(f^{-1}(x)=\dfrac{x+7}{5}\).
\(x\le0\Rightarrow f^{-1}(x)=-\sqrt{x+4}\); \(x\ge0\Rightarrow f^{-1}(x)=\sqrt{x+4}\).
\(f^{-1}(x)=\dfrac{x-3}{x-2}\), domínios: \(x\neq1\) (para a inversa); em \(f\), \(x\neq1\).
\(f^{-1}(x)=\sqrt[3]{x-1}\).
\(f^{-1}(x)=\log_2 x\), com \(x>0\) e imagem \(\mathbb{R}\).

12) Continue estudando

Revisão
Relembre bases importantes: Funções, Função Composta, Função Exponencial, Função Logarítmica.

Mapas Mentais 10 eBooks ENEM Matemática Canais Oficiais

13) Perguntas frequentes (FAQ)

Como sei se uma função tem inversa?

Verifique a injetividade (teste da reta horizontal). Se necessário, restrinja o domínio. A bijetividade garante inversa bem definida.

O que acontece se a função não for injetiva?

Sem injetividade, a “inversa” não será função. Mas muitas vezes basta limitar o domínio para obter inversa.

Qual a relação com logaritmos e exponenciais?

\(a^x\) e \(\log_a x\) são inversas (com \(a>0, a\neq1\)), espelhadas em \(y=x\).

🔗 Links internos: Funções • Função composta • Função exponencial • Função logarítmica

Lista de Exercícios — Função Inversa

Fácil 1 Encontre \(f^{-1}\) de \(f(x)=3x+5\).

\(y=3x+5\Rightarrow x=\dfrac{y-5}{3}\Rightarrow \boxed{f^{-1}(x)=\dfrac{x-5}{3}}.\)

Fácil 2 Encontre \(f^{-1}\) de \(f(x)=\dfrac{x-2}{4}\).

\(y=\dfrac{x-2}{4}\Rightarrow 4y=x-2\Rightarrow x=4y+2\Rightarrow \boxed{f^{-1}(x)=4x+2}.\)

Fácil 3 Encontre \(f^{-1}\) de \(f(x)=2x-7\).

\(y=2x-7\Rightarrow x=\dfrac{y+7}{2}\Rightarrow \boxed{f^{-1}(x)=\dfrac{x+7}{2}}.\)

Fácil 4 Encontre \(f^{-1}\) de \(f(x)=5-2x\).

\(y=5-2x\Rightarrow 2x=5-y\Rightarrow x=\dfrac{5-y}{2}\Rightarrow \boxed{f^{-1}(x)=\dfrac{5-x}{2}}.\)

Fácil 5 \(f(x)=\dfrac{3}{x}\) (domínio \(x\ne0\)). Encontre \(f^{-1}\) e seu domínio.

\(y=\dfrac{3}{x}\Rightarrow xy=3\Rightarrow x=\dfrac{3}{y}\Rightarrow \boxed{f^{-1}(x)=\dfrac{3}{x}},\) domínio \(x\ne0\). (Autoinversa.)

Interm. 6 \(f(x)=\dfrac{2x+1}{x-3}\) (dom. \(x\ne3\)). Encontre \(f^{-1}\) e o domínio de \(f^{-1}\).

\(y=\dfrac{2x+1}{x-3}\Rightarrow y(x-3)=x+1\Rightarrow x(y-1)=3y+1\Rightarrow x=\dfrac{3y+1}{y-1}.\) Logo, \(\boxed{f^{-1}(x)=\dfrac{3x+1}{x-2}}\) com domínio \(x\ne2\).

Interm. 7 \(f(x)=\sqrt{x+4}\) (dom. \(x\ge-4\)). Encontre \(f^{-1}\) e o domínio de \(f^{-1}\).

\(y=\sqrt{x+4}\Rightarrow x=y^2-4\Rightarrow \boxed{f^{-1}(x)=x^2-4}\) com domínio \(x\ge0\).

Interm. 8 \(f(x)=x^2+2\) com restrição \(x\ge0\). Encontre \(f^{-1}\) e seu domínio.

\(y=x^2+2\Rightarrow x=\sqrt{y-2}\Rightarrow \boxed{f^{-1}(x)=\sqrt{x-2}}\) com domínio \(x\ge2\).

Interm. 9 \(f(x)=2^x\). Encontre \(f^{-1}\) e seu domínio.

\(\boxed{f^{-1}(x)=\log_2 x}\) com domínio \(x>0\).

Interm. 10 \(f(x)=\log_3(x-1)\) (dom. \(x>1\)). Encontre \(f^{-1}\).

\(y=\log_3(x-1)\Rightarrow x-1=3^y\Rightarrow \boxed{f^{-1}(x)=3^x+1}.\)

Avanç. 11 \(f(x)=\dfrac{x^2+1}{x-1}\) (dom. \(x\ne1\)). Ramos de inversa.

\(y=\dfrac{x^2+1}{x-1}\Rightarrow y(x-1)=x^2+1\Rightarrow x^2-yx+(1+y)=0\). \(\displaystyle x=\frac{y\pm\sqrt{(y-2)^2-8}}{2}\). Como \(f\) não é monotônica em todo o domínio, restrinja a intervalos onde seja estritamente crescente/decrescente (ex.: \(x\ge 1+\sqrt2\) ou \(x\le 1-\sqrt2\)) para obter ramos de \(f^{-1}\).

Avanç. 12 \(f(x)=e^{2x+1}\). Encontre \(f^{-1}\).

\(y=e^{2x+1}\Rightarrow \ln y=2x+1\Rightarrow \boxed{f^{-1}(x)=\dfrac{\ln x-1}{2}},\ x>0.\)

Avanç. 13 \(f(x)=\sqrt[3]{\,2x-5\,}\). Encontre \(f^{-1}\).

\(y^3=2x-5\Rightarrow x=\dfrac{y^3+5}{2}\Rightarrow \boxed{f^{-1}(x)=\dfrac{x^3+5}{2}}.\)

Avanç. 14 \(f(x)=x^3+3x+1\). Mostre que é bijetora e conclua sobre a inversa.

\(f'(x)=3x^2+3>0\ \forall x\Rightarrow f\) estritamente crescente \(\Rightarrow\) bijetora em \(\mathbb{R}\). A inversa \(f^{-1}\) existe e é única (sem forma elementar fechada).

Avanç. 15 \(f(x)=\dfrac{\ln x}{1+\ln x}\) (dom. \(x>0,\ x\ne e^{-1}\)). Imagem e \(f^{-1}\).

Seja \(y=\dfrac{L}{1+L}\) com \(L=\ln x\). Então \(y(1+L)=L\Rightarrow y=L(1-y)\Rightarrow L=\dfrac{y}{1-y}\). \(\boxed{f^{-1}(x)=e^{\frac{x}{1-x}}}\) com domínio \(x\ne1\). A imagem de \(f\) é \((-\infty,1)\cup(1,\infty)\).

Aplic. 16 Conversão \(F=\dfrac{9}{5}C+32\). Encontre \(C(F)\).

\(C=\dfrac{5}{9}(F-32)\Rightarrow \boxed{C(F)=\dfrac{5}{9}(F-32)}.\)

Aplic. 17 Preço com desconto \(f(x)=x(1-p)\) (\(0

\(y=x(1-p)\Rightarrow x=\dfrac{y}{1-p}\Rightarrow \boxed{f^{-1}(x)=\dfrac{x}{1-p}}.\)

Aplic. 18 População \(f(t)=500\cdot 2^t\) (t em horas). Encontre \(t(y)\).

\(y=500\cdot 2^t\Rightarrow \boxed{t=\log_2\!\left(\dfrac{y}{500}\right)},\ y>0.\)

Aplic. 19 Velocidade \(v(t)=9{,}8\,t\). Encontre \(t(v)\).

\(\boxed{t=\dfrac{v}{9{,}8}}.\)

Aplic. 20 Custo \(C(q)=50\ln(q)+200\) (dom. \(q>0\)). Encontre \(q(x)\).

\(x=50\ln q+200\Rightarrow \boxed{q=e^{\frac{x-200}{50}}},\ q>0.\)

Gabarito rápido: 1) \((x-5)/3\) • 2) \(4x+2\) • 3) \((x+7)/2\) • 4) \((5-x)/2\) • 5) \(3/x\) • 6) \((3x+1)/(x-2)\) • 7) \(x^2-4\) (dom \(x\ge0\)) • 8) \(\sqrt{x-2}\) (dom \(x\ge2\)) • 9) \(\log_2 x\) (dom \(x>0\)) • 10) \(3^x+1\) • 11) ramos via \(x=\frac{y\pm\sqrt{(y-2)^2-8}}{2}\) • 12) \((\ln x-1)/2\) • 13) \((x^3+5)/2\) • 14) bijetora (inversa existe) • 15) \(e^{x/(1-x)}\) (dom \(x\ne1\)) • 16) \(\frac{5}{9}(F-32)\) • 17) \(x/(1-p)\) • 18) \(\log_2(y/500)\) • 19) \(v/9{,}8\) • 20) \(e^{(x-200)/50}\).

Relacionadas

Função Afim ou ou do 1º Grau

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.