A função logarítmica é o inverso da função exponencial e tem papel fundamental no estudo da matemática, especialmente em equações, gráficos e aplicações reais, como escalas logarítmicas e cálculos financeiros.

O que é uma Função Logarítmica?

Chamamos de função logarítmica a função da forma:

f(x) = log_a(x)

Onde:

• a é a base do logaritmo, com a > 0 e a ≠ 1;
• x é um número real positivo (x > 0).

A função logarítmica responde à pergunta: “qual o expoente que devo aplicar à base a para obter x?”

Exemplo: log₂(8) = 3 → pois 2³ = 8

Domínio, Imagem e Gráfico

• Domínio: x > 0
• Imagem: todos os números reais ℝ
• Ponto notável: (1, 0), pois log_a(1) = 0
• Assíntota vertical: no eixo y (x = 0)

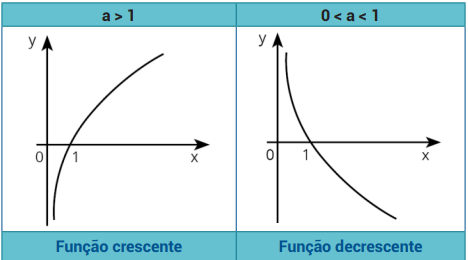
Comportamento do gráfico:

• Se a > 1: função crescente
• Se 0 < a < 1: função decrescente

Propriedades dos Logaritmos

• log_a(1) = 0
• log_a(a) = 1
• log_a(x·y) = log_a(x) + log_a(y)
• log_a(x/y) = log_a(x) – log_a(y)
• log_a(xⁿ) = n·log_a(x)

Exemplos de Funções Logarítmicas

Exemplo 1:

f(x) = log₂(x)
Função logarítmica de base 2, crescente, domínio x > 0.

Exemplo 2:

f(x) = log_1/2(x)
Função decrescente, base entre 0 e 1. Também definida para x > 0.

Exemplo 3:

f(x) = log(x)
Forma comum de escrever log₁₀(x), base 10.

Exercícios Resolvidos

Exercício 1

Calcule: log₁₀(1000)

Solução: 10³ = 1000 → Resposta: 3

Exercício 2

Calcule: log₂(1/8)

Solução: 2⁻³ = 1/8 → Resposta: -3

Exercício 3

Determine o valor de log₃(81)

Solução: 81 = 3⁴ → Resposta: 4

Exercício 4

Simplifique: log₅(25) + log₅(4)

Solução: log₅(25·4) = log₅(100) → Resposta: 2

Exercício 5

Resolva: log₃(x) = 2

Solução: 3² = x → x = 9

Conclusão

A função logarítmica é indispensável para resolver equações exponenciais e para interpretar fenômenos que envolvem crescimento desacelerado. Dominar esse conteúdo é essencial para quem busca se destacar em matemática.

Continue seus estudos com nossos artigos sobre Função Exponencial e Função Racional.