Intercepto no eixo y da parábola (função quadrática)
O intercepto no eixo y (ou interseção com o eixo \(Oy\)) de uma parábola é o ponto do gráfico de \(f(x)=ax^2+bx+c\) onde \(x=0\). Por definição:
Ou seja, o intercepto em \(y\) é sempre o ponto \((0,c)\). Se \(c>0\), fica acima do eixo \(x\); se \(c<0\), fica abaixo; se \(c=0\), o gráfico passa pela origem \((0,0)\).
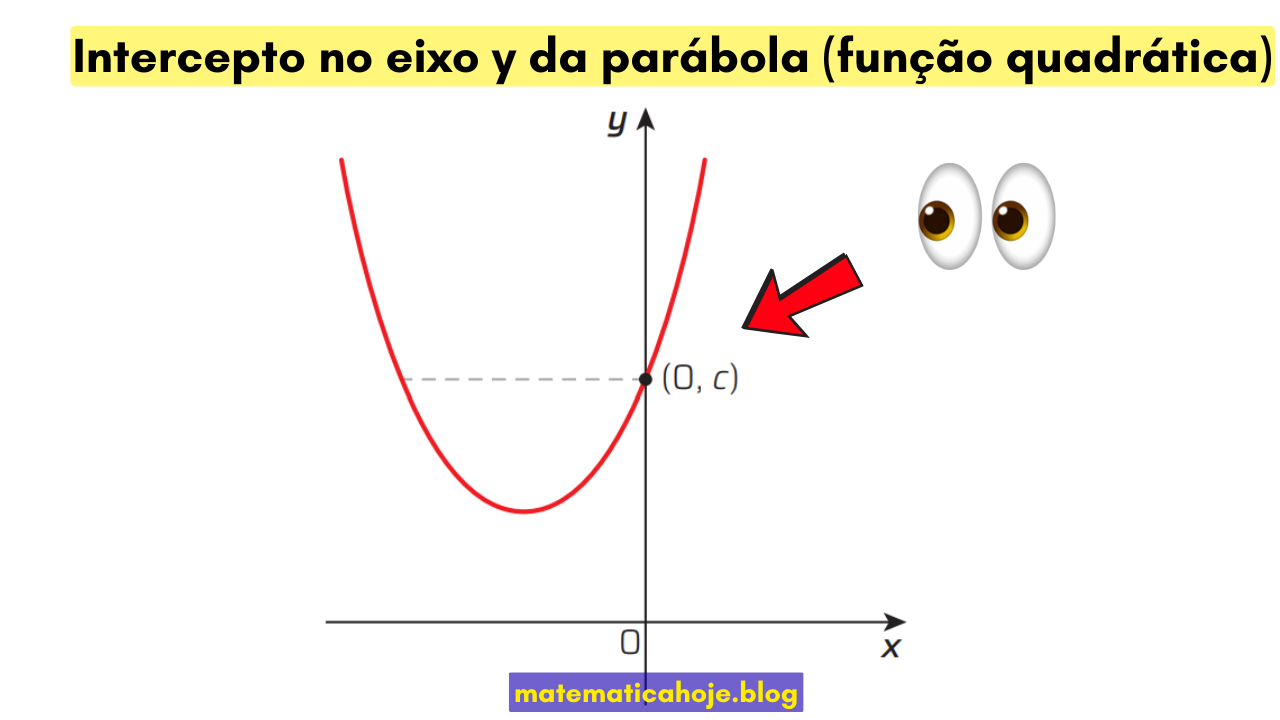
Como achar o intercepto em y nas diferentes formas
Forma padrão \(ax^2+bx+c\)
Substitua \(x=0\):
Forma canônica \(a(x-h)^2+k\)
Use \(x=0\):
O intercepto é \((0,\,a h^2 + k)\).
Forma fatorada \(a(x-x_1)(x-x_2)\)
Novamente \(x=0\):
Logo \(c=a\,x_1x_2\) (coerente com as relações de Viète).
📘 E-book de Fórmulas de Matemática
Tenha à mão \(f(0)=c\), forma canônica, vértice, Bhaskara e mais — perfeito para revisão rápida.
Baixar agoraExemplos resolvidos (com as contas em coluna)
Exemplo 1 — \(f(x)=2x^2-3x+5\)
Intercepto em \(y\):
Ponto \((0,5)\). Aqui, \(c=5\).
Exemplo 2 — \(g(x)=3(x-2)^2-4\)
Forma canônica:
Intercepto \((0,8)\).
Exemplo 3 — \(h(x)=-2(x+1)(x-3)\)
Forma fatorada:
Intercepto \((0,6)\). Note que \(c=a\,x_1x_2=-2\cdot(-1)\cdot 3=6\).
Exemplo 4 (interpretação física) — Altura de um objeto
Um lançamento vertical é modelado por \(h(t)=-5t^2+20t+1{,}5\) (unidades SI). A altura inicial é o intercepto em \(y\):
Leituras úteis e conexões
- Coeficientes \(b\) e \(c\): como \(c\) desloca o gráfico no eixo \(y\).
- Zeros da quadrática: intercepto em \(y\) não é raiz (a menos que \(c=0\)).
- Vértice e máximo/mínimo: como o “pico” ou “vale” se relaciona com \(c\) e \(a\).
- Construção do gráfico: tabelas, vértice e interceptos.
Erros comuns
- Confundir intercepto em \(y\) com raízes: raízes são onde \(y=0\); intercepto em \(y\) é onde \(x=0\).
- Esquecer o sinal de \(c\): ele indica se o ponto \((0,c)\) está acima ou abaixo do eixo \(x\).
- Trocar formas: em \(a(x-h)^2+k\), o intercepto é \(a h^2 + k\), não “\(k\)” (a menos que \(h=0\)).
Exercícios propostos
1) Determine o intercepto em \(y\) de \(f(x)=\tfrac12 x^2-4x-3\).
Ver solução
Ponto \((0,-3)\).
2) Para \(g(x)=2(x+3)^2-5\), encontre o intercepto em \(y\).
Ver solução
Ponto \((0,13)\).
3) Dada \(h(x)=-3(x-1)(x+2)\), calcule \(f(0)\).
Ver solução
Ponto \((0,6)\).













