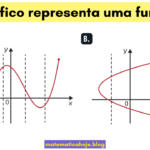
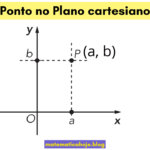
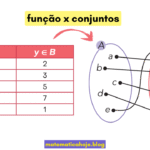
Quais são as funções fundamentais e como reconhecê-las?
As funções fundamentais são a base de quase todo o estudo de Matemática no ensino médio e nos vestibulares. Este guia reúne as famílias mais importantes, explica o “desenho” do gráfico, mostra propriedades essenciais e traz exemplos resolvidos passo a passo — com as contas sempre uma abaixo da outra após o sinal de igualdade para facilitar a leitura no celular. Ao final, há uma lista de exercícios com solução em sistema abre/fecha.
Baixe grátis: eBook Fórmulas de Matemática — um PDF prático para revisão rápida.
Panorama geral: famílias de funções e seus comportamentos
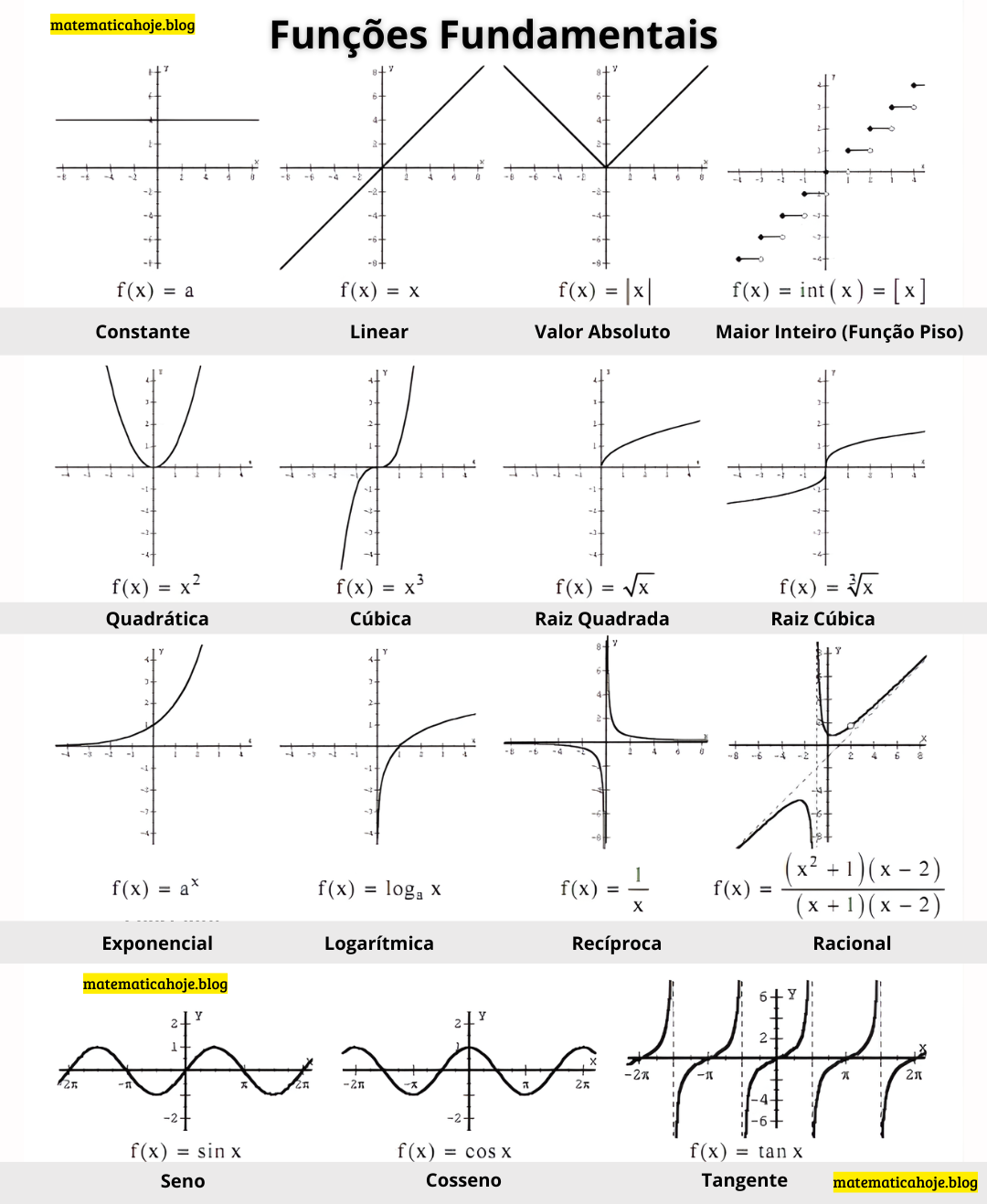
Veja a lista organizada por tipo. Use-a como mapa de estudos:
| Família | Modelo | Observações rápidas |
|---|---|---|
| Constante | \(f(x)=a\) | Reta horizontal; não depende de \(x\). |
| Linear | \(f(x)=mx+b\) | Cresce/decresce conforme o coeficiente angular \(m\). |
| Valor Absoluto | \(f(x)=|x|\) | Gráfico em “V”; simetria em relação ao eixo \(y\). |
| Maior Inteiro (piso) | \(f(x)=\lfloor x\rfloor\) | Grafia em “degraus”; salta nos inteiros. |
| Quadrática | \(f(x)=ax^2+bx+c\) | Parábola; vértice, concavidade e raízes pelo discriminante. |
| Cúbica | \(f(x)=ax^3+bx^2+cx+d\) | Curva em “S”; pode ter até 3 raízes reais. |
| Raiz Quadrada | \(f(x)=\sqrt{x}\) | Domínio \(x\ge 0\); cresce e “achata”. |
| Raiz Cúbica | \(f(x)=\sqrt[3]{x}\) | Definida para todo real; é ímpar. |
| Exponencial | \(f(x)=a^x\;(a>0, a\neq1)\) | Crescimento ou decaimento; base determina o sentido. |
| Logarítmica | \(f(x)=\log_a x\) | Inversa da exponencial; domínio \(x>0\). |
| Recíproca | \(f(x)=\frac{1}{x}\) | Assíntotas nos eixos; não definida em \(x=0\). |
| Racional | \(f(x)=\dfrac{p(x)}{q(x)}\) | Assíntotas e buracos conforme zeros de \(q(x)\). |
| Trigonométricas | \(\sin x,\ \cos x,\ \tan x\) | Períodos e propriedades de simetria. |
Estude com diagramas prontos: Mapas Mentais de Matemática
Modelos essenciais: definições, gráficos e aplicações práticas
Reta constante e função linear no contexto do dia a dia
Exemplo (Linear): preço com taxa fixa
Um serviço cobra taxa fixa de R$ 10 e mais R$ 3 por item: \(f(x)=3x+10\).
👀 Solução passo a passo (quanto custa 8 itens?)
$$
f(8)=3\cdot 8+10 \\
= 24+10 \\
= 34
$$
Logo, o custo é R$ 34.
Valor absoluto: distância até a origem e “gráfico em V”
Exemplo (|x|): distância na reta
Qual a distância entre \(x=-7\) e a origem?
👀 Solução passo a passo
$$
d=|-7| \\
= 7
$$
Distância igual a 7 unidades.
Função piso (maior inteiro) e tabelas de cobrança em degraus
Exemplo (piso): tarifa por faixa
Uma garagem cobra R$ 5 por hora cheia. Para 2,3 h, quanto pagar?
👀 Solução passo a passo
$$
\text{Horas cobradas}=\lfloor 2{,}3 \rfloor \\
= 2 \\
\text{Total}=2\cdot 5 \\
= 10
$$
Valor devido: R$ 10.
Parábola quadrática: concavidade, vértice e raízes
Exemplo (x²): raízes de \(x^2-5x+6\)
👀 Solução passo a passo
$$
\Delta=b^2-4ac \\
= (-5)^2-4\cdot 1\cdot 6 \\
= 25-24 \\
= 1
$$
$$
x=\frac{5\pm \sqrt{1}}{2} \\
= \frac{5\pm 1}{2}
$$
$$
x_1=\frac{6}{2}=3 \\
x_2=\frac{4}{2}=2
$$
Curva cúbica: ponto de inflexão e comportamento em S
Exemplo (x³): sinal de \(f(x)=x^3-8\)
👀 Solução passo a passo
$$
x^3-8=0 \\
x^3=8 \\
x=2
$$
Para \(x>2\), \(f(x)>0\); para \(x<2\), \(f(x)<0\).
Raiz quadrada e raiz cúbica: domínio e monotonicidade
Exemplo (\(\sqrt{x}\))
👀 Solução passo a passo
$$
f(25)=\sqrt{25} \\
= 5
$$
Exponenciais e logaritmos: crescimento, inversa e aplicações
Exemplo (exponencial): \(f(x)=2^x\)
👀 Solução passo a passo (encontre \(x\) tal que \(2^x=32\))
$$
2^x=32 \\
32=2^5 \\
x=5
$$
Exemplo (log): \(\log_2 64\)
👀 Solução passo a passo
$$
\log_2 64=x \\
2^x=64 \\
64=2^6 \\
x=6
$$
Funções recíprocas e racionais: assíntotas e restrições
Exemplo (recíproca): \(f(x)=\frac{1}{x}\)
👀 Solução passo a passo (valor em \(x=-\tfrac{1}{2}\))
$$
f\!\left(-\frac{1}{2}\right)=\frac{1}{-\frac{1}{2}} \\
= -2
$$
Exemplo (racional): domínio de \(\dfrac{x^2+1}{x-2}\)
👀 Solução passo a passo
$$
x-2\neq 0 \\
x\neq 2
$$
Logo, o domínio é \(\mathbb{R}\setminus\{2\}\).
Trigonométricas básicas: seno, cosseno e tangente
Exemplo (\(\sin x\))
👀 Solução passo a passo
$$
\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}
$$
Reforce seus estudos: ENEM Matemática | Coleção 10 eBooks | Banco de Questões
Lista de exercícios comentados sobre funções fundamentais
Exercício 1 — Linear: calcule \(f(12)\) para \(f(x)=4x-7\)
Enunciado. Para a função linear \(f(x)=4x-7\), determine \(f(12)\).
Solução.
$$ f(12)=4\cdot 12-7 \\ = 48-7 \\ = 41 $$
Solução.
$$ f(12)=4\cdot 12-7 \\ = 48-7 \\ = 41 $$
Exercício 2 — Valor absoluto: resolva \(|x-5|=9\)
Enunciado. Resolva a equação \(|x-5|=9\).
Solução.
$$ x-5=9\ \ \text{ou}\ \ x-5=-9 \\ x=14\ \ \text{ou}\ \ x=-4 $$
Solução.
$$ x-5=9\ \ \text{ou}\ \ x-5=-9 \\ x=14\ \ \text{ou}\ \ x=-4 $$
Exercício 3 — Quadrática: raízes de \(x^2-3x-10=0\)
Enunciado. Encontre as raízes de \(x^2-3x-10=0\).
Solução.
$$ \Delta=b^2-4ac \\ = (-3)^2-4\cdot 1\cdot(-10) \\ = 9+40 \\ = 49 $$ $$ x=\frac{3\pm \sqrt{49}}{2} \\ = \frac{3\pm 7}{2} $$ $$ x_1=\frac{10}{2}=5 \\ x_2=\frac{-4}{2}=-2 $$
Solução.
$$ \Delta=b^2-4ac \\ = (-3)^2-4\cdot 1\cdot(-10) \\ = 9+40 \\ = 49 $$ $$ x=\frac{3\pm \sqrt{49}}{2} \\ = \frac{3\pm 7}{2} $$ $$ x_1=\frac{10}{2}=5 \\ x_2=\frac{-4}{2}=-2 $$
Exercício 4 — Exponencial: resolva \(3^x=81\)
Enunciado. Determine \(x\) tal que \(3^x=81\).
Solução.
$$ 81=3^4 \\ 3^x=3^4 \\ x=4 $$
Solução.
$$ 81=3^4 \\ 3^x=3^4 \\ x=4 $$
Exercício 5 — Logaritmo: calcule \(\log_5 125\)
Enunciado. Calcule o valor de \(\log_5 125\).
Solução.
$$ \log_5 125=x \\ 5^x=125 \\ 125=5^3 \\ x=3 $$
Solução.
$$ \log_5 125=x \\ 5^x=125 \\ 125=5^3 \\ x=3 $$
Exercício 6 — Recíproca: avalie \(f(-4)\) em \(f(x)=\tfrac{1}{x}\)
Enunciado. Para \(f(x)=\tfrac{1}{x}\), determine \(f(-4)\).
Solução.
$$ f(-4)=\frac{1}{-4} \\ = -\frac{1}{4} $$
Solução.
$$ f(-4)=\frac{1}{-4} \\ = -\frac{1}{4} $$
Exercício 7 — Racional: domínio de \(\dfrac{2x+1}{x^2-9}\)
Enunciado. Encontre o domínio de \(f(x)=\dfrac{2x+1}{x^2-9}\).
Solução.
$$ x^2-9\neq 0 \\ (x-3)(x+3)\neq 0 \\ x\neq 3\ \text{e}\ x\neq -3 $$
Solução.
$$ x^2-9\neq 0 \\ (x-3)(x+3)\neq 0 \\ x\neq 3\ \text{e}\ x\neq -3 $$
Domínio: \(\mathbb{R}\setminus\{-3,\,3\}\).
Exercício 8 — Trigonometria: \(\sin\left(\tfrac{\pi}{3}\right)\)
Enunciado. Calcule \(\sin\left(\tfrac{\pi}{3}\right)\).
Solução.
$$ \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2} $$
Solução.
$$ \sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2} $$
Conclusão: como fixar os gráficos e reconhecer padrões
Dominar as funções fundamentais é reconhecer formas e padrões recorrentes: retas, parábolas, curvas em S, degraus, assíntotas e ondas periódicas. Pratique com variações de parâmetros, refaça os exercícios e use os links indicados para revisar fórmulas e treinar com questões.
Perguntas frequentes (FAQ)
Qual é a diferença entre função linear e afim?
A linear pura é do tipo \(f(x)=mx\) (passa pela origem). A função afim é \(f(x)=mx+b\),
com termo constante \(b\) que desloca a reta para cima ou para baixo, sem alterar a inclinação.
Como identificar rapidamente o gráfico de uma quadrática?
Observe o coeficiente de \(x^2\) para a concavidade e use o discriminante \(\Delta\) para saber
se há 0, 1 ou 2 raízes reais. O vértice pode ser obtido por \((-b/2a, -\Delta/4a)\).
Quando usar logaritmo em vez de exponencial?
Use logaritmos para “trazer o expoente para baixo”, resolvendo equações em que a incógnita está
no expoente. Como são funções inversas, você pode converter \(a^x=b\) em \(x=\log_a b\).
O que são assíntotas em funções racionais e recíprocas?
São linhas às quais o gráfico se aproxima, mas não toca. Em \(1/x\), os eixos são assíntotas.
Em racionais, raízes do denominador geram assíntotas verticais e o grau relativo define a horizontal/oblíqua.
Autor: Adriano Rocha
