Funções Trigonométricas: Um Guia Completo

As funções trigonométricas são fundamentais em várias áreas da matemática e ciências aplicadas. Elas surgem originalmente do estudo de triângulos e têm aplicações extensivas em física, engenharia, astronomia e outras disciplinas. Neste artigo, exploraremos as seis principais funções trigonométricas: seno, cosseno, tangente, secante, cossecante e cotangente. Veremos suas definições, propriedades, gráficos e aplicações.

Definição das Funções Trigonométricas

As funções trigonométricas básicas são definidas usando um triângulo retângulo, mas elas também podem ser entendidas no contexto do círculo trigonométrico (ou unitário), onde o círculo tem raio 1 e está centrado na origem do plano cartesiano.

1. Seno (sin⁡θ)

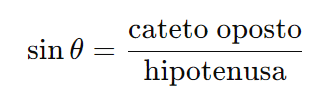
No círculo trigonométrico, sin⁡θ é a coordenada y do ponto na circunferência correspondente ao ângulo θ.

2. Cosseno (cos⁡θ)

No círculo trigonométrico, cos⁡θ é a coordenada x do ponto correspondente ao ângulo θ.

3. Tangente (tan⁡θ)

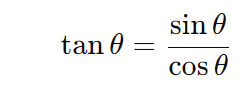
Geometricamente, no círculo trigonométrico, a tangente é a razão entre a coordenada y (sin⁡θ) e a coordenada x (cos⁡θ) do ponto na circunferência.

4. Secante (sec⁡θ)

A secante de um ângulo θ é a inversa do cosseno

5. Cossecante (csc⁡θ)

A cossecante de um ângulo θ é a inversa do seno

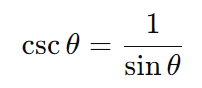
6. Cotangente (cot⁡θ)

A cotangente de um ângulo θ é a inversa da tangente.

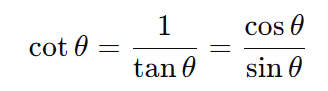
Propriedades das Funções Trigonométricas

As funções trigonométricas têm várias propriedades importantes que as tornam ferramentas poderosas na análise matemática.

1. Período

As funções seno e cosseno são periódicas com período 2π. Isso significa que seus valores se repetem a cada 2π radianos ou 360 graus.

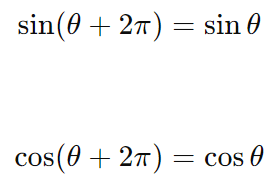
A tangente e cotangente têm período π:

2. Paridade

As funções seno e tangente são funções ímpares, enquanto cosseno e secante são funções pares:

• Funções ímpares:

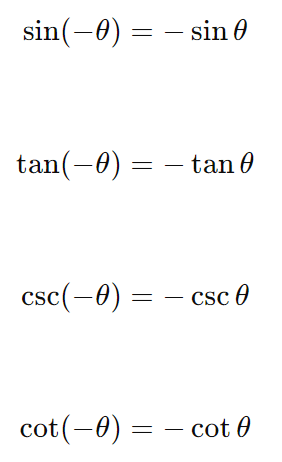
Funções pares:

3. Relações Fundamentais

Além das identidades trigonométricas básicas, como sin^⁡2θ + cos⁡²θ = 1, as funções trigonométricas também estão inter-relacionadas por outras identidades importantes, como:

• Relação entre seno e cosseno:

• Relação entre tangente e secante:

• Relação entre cotangente e cossecante:

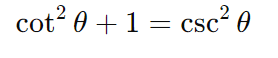
Gráficos das Funções Trigonométricas

Cada função trigonométrica possui um gráfico característico que reflete suas propriedades.

Os gráficos das funções trigonométricas são fundamentais para entender como essas funções se comportam em diferentes intervalos de valores de θ\thetaθ. Esses gráficos possuem padrões distintos que refletem a natureza periódica das funções seno, cosseno, tangente, cotangente, secante e cossecante. A seguir, detalhamos as características principais dos gráficos de cada uma dessas funções.

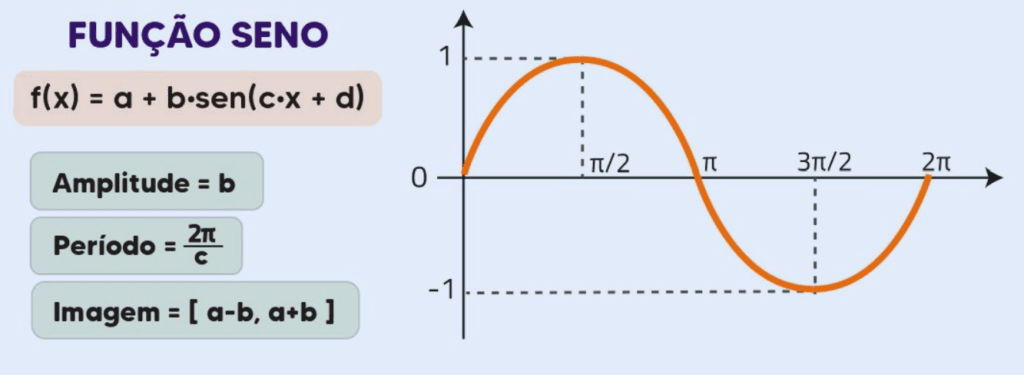
1. Gráfico da Função Seno (sin⁡θ)

Características:

• Forma: O gráfico de sin⁡θ é uma onda senoidal, que se repete a cada 2π radianos (ou 360°).
• Amplitude: O valor máximo e mínimo que sin⁡θ pode alcançar é 1 e -1, respectivamente.
• Período: O período da função seno é 2π, o que significa que a função repete seu padrão a cada 2π unidades.
• Zeros: O gráfico cruza o eixo x em múltiplos de π (ou seja, em θ=0,π,2π,…).
• Simetria: sin⁡θ é uma função ímpar, o que significa que seu gráfico é simétrico em relação à origem (sin⁡(−θ)=−sin⁡(θ))

Gráfico f(x) = senθ

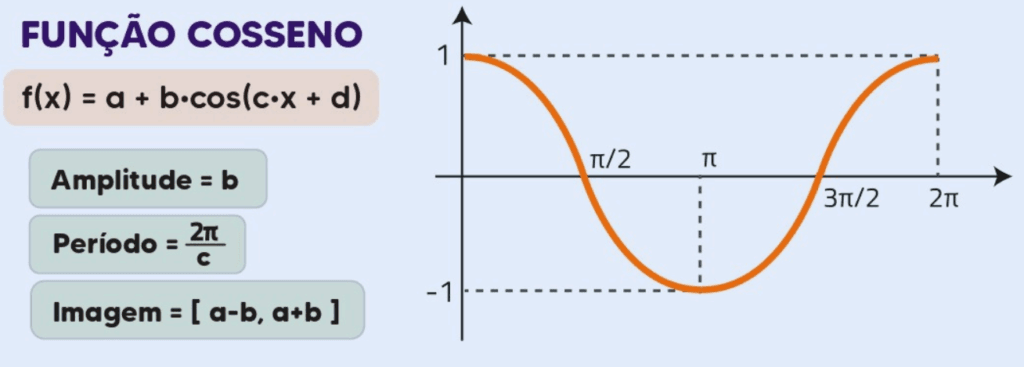
2. Gráfico da Função Cosseno (cos⁡θ)

Características:

• Forma: O gráfico de cos⁡θ também é uma onda senoidal, mas deslocada em relação ao seno.
• Amplitude: Assim como o seno, o cosseno varia entre 1 e -1.
• Período: O período da função cosseno é 2π.
• Zeros: O gráfico cruza o eixo x em θ=π/2,3π/2,5π/2,…
• Simetria: cos⁡θ é uma função par, sendo simétrica em relação ao eixo y (cos⁡(−θ)=cos⁡(θ)).

Gráfico f(x) = cosθ

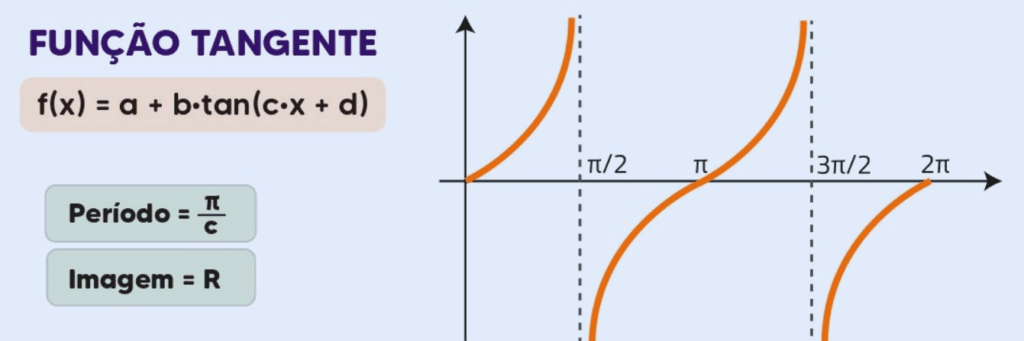
3. Gráfico da Função Tangente (tan⁡θ)

Características:

• Forma: O gráfico de tan⁡θ tem uma forma repetitiva que consiste em curvas ascendentes, com assintotas verticais onde a função não está definida.
• Amplitude: A tangente não tem amplitude fixa, já que pode assumir valores muito grandes (positivos ou negativos).
• Período: O período da função tangente é π.
• Zeros: O gráfico cruza o eixo xxx em múltiplos de π (θ=0,π,2π,…).
• Assimptotas: As assintotas verticais ocorrem em θ=π/2+kπ (onde k é um inteiro).
• Simetria: tan⁡θ é uma função ímpar (tan⁡(−θ)=−tan⁡(θ)).

Gráfico f(x) = tanθ

Conclusão

Os gráficos das funções trigonométricas são representações visuais que nos permitem compreender melhor o comportamento dessas funções ao longo de diferentes intervalos. A natureza periódica dessas funções, combinada com suas propriedades de simetria e as posições de suas assimptotas e zeros, faz com que esses gráficos sejam ferramentas essenciais na análise de fenômenos que envolvem ângulos, ciclos e movimentos repetitivos.